文章目录
- 快速排序的非递归
- 三数取中法选取key
- 快速排序三路划分
- 归并排序的递归
- 归并排序的非递归
- 计数排序
- 稳定性
- 排序算法的时间复杂度
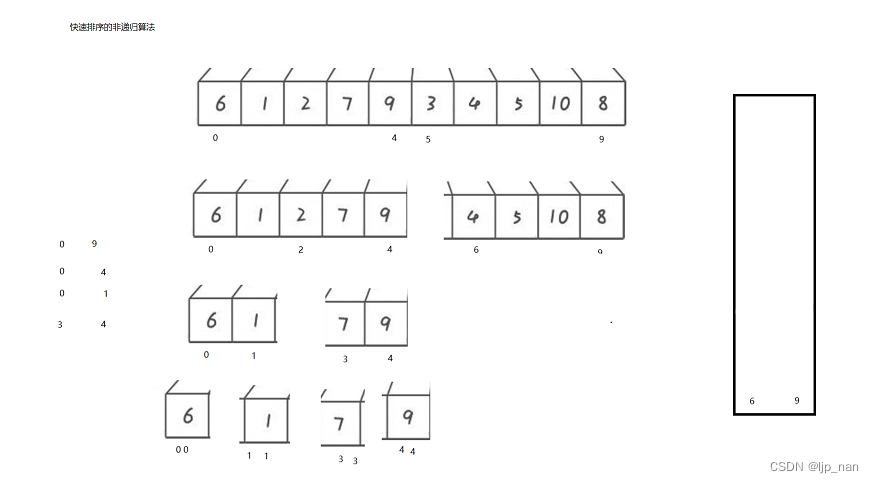
快速排序的非递归
我们使用一个栈来模拟函数的递归过程,这里就是在利用栈分区间。把一个区间分为 [left,keyi-1][key][keyi+1,right]递归下去,直至区间不存在或left > right。
如图所示:
先把整体的区间压进去,然后出栈,处理完毕后找到keyi再分为左右两个区间。然后往栈里压有区间,压左区间,就像树的后续遍历一样先把叶子区间处理,再处理分支节点的区间。
代码如下所示:
void QuickSortNonS(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, left);
STPush(&st, right);
while (!STEmpty(&st))
{
int right = STTop(&st);
STPop(&st);
int left = STTop(&st);
STPop(&st);
int keyi = PastSort1(a, left, right);
//先入右区间
if (keyi + 1 < right)
{
STPush(&st, keyi + 1);
STPush(&st, right);
}
//再入左区间
if (keyi - 1 > left)
{
STPush(&st, left);
STPush(&st, keyi - 1);
}
}
STDestory(&st);
}
三数取中法选取key
还可以选择三数取中法来选取key的值,原理是选取不大不小的数使得快速排序的交换次数变少。
代码如下:
//三数取中法选取Key
int GetMidKey(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] <= a[right]&&a[left] <= a[mid] && a[mid] <= a[right])
{
return mid;
}
else if(a[left]<=a[mid]&&a[left]<=a[right]&&a[left]<=a[mid])
{
return right;
}
else if (a[right]<=a[mid]&&a[right]<=a[left]&&a[left]<=a[mid])
{
return left;
}
else if (a[mid] <= a[left] && a[mid] <= a[right] && a[right] <= a[left])
{
return right;
}
else if (a[mid] <= a[right] && a[mid] <= a[left] && a[left] <= a[right])
{
return left;
}
else if (a[right] <= a[left] && a[right] <= a[mid] && a[mid] <= a[left])
{
return mid;
}
else
{
return left;
}
}
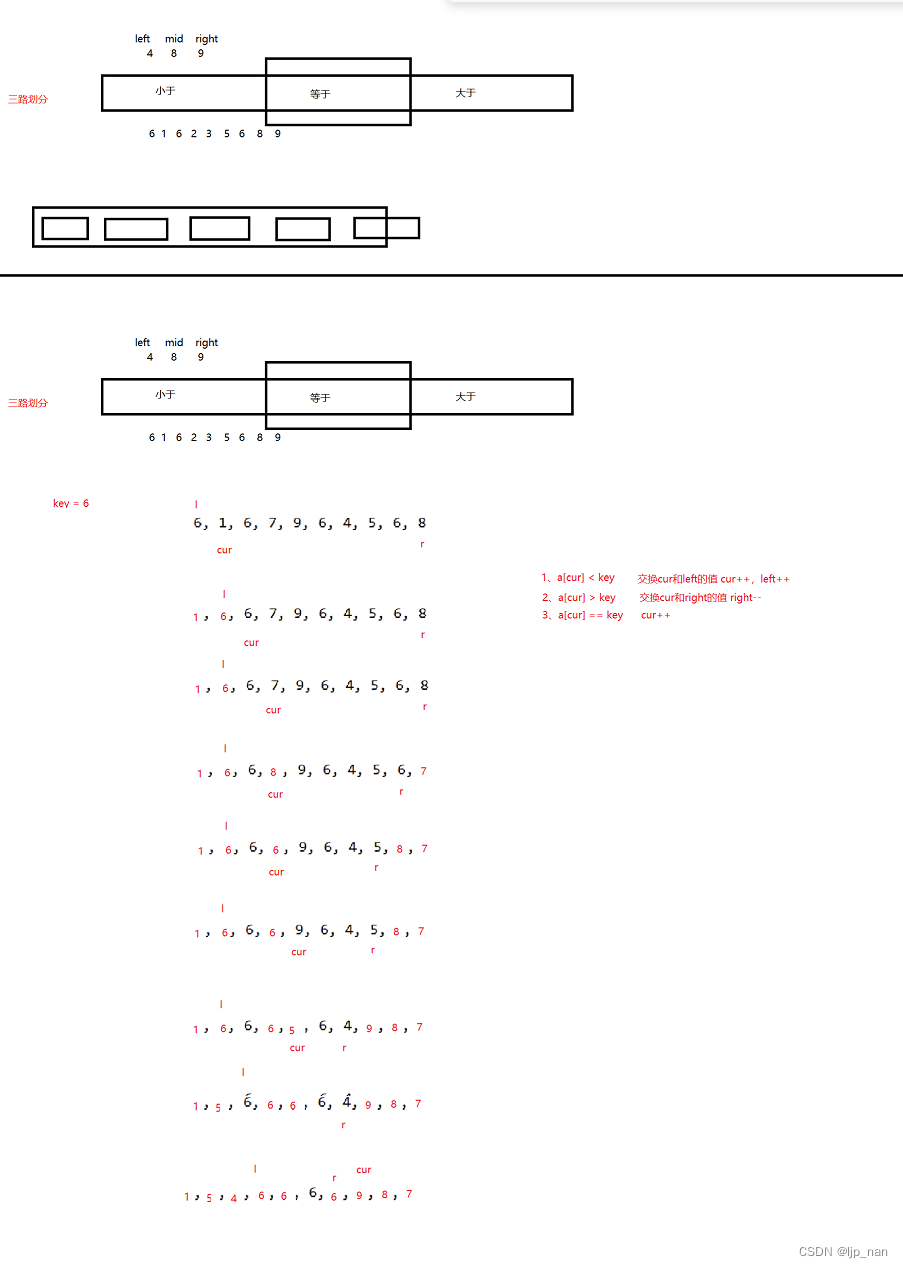
快速排序三路划分
原理:规定左指针,cur指针,右指针。当a[cur] < key时,把a[cur]和a[left]的值交换cur++,left++。当a[cur] > key时,把a[cur]和a[right]的值交换,right–。当a[cur] > key时,cur++,具体的操作过程如下图所示:
代码如下:
//三路划分
//1、最小的在最左边
//2、最大的在最右边
//3、相等的在中间
void QuickSort1(int* a, int begin, int end)
{
if (begin > end)
{
return;
}
//三路划分
int keyi = GetMidKey(a, begin, end);
Swap(&a[begin], &a[keyi]);
int key = a[begin];
int left = begin;
int right = end;
int cur = left + 1;
while (cur <= right)
{
if (a[cur] < key)
{
Swap(&a[cur], &a[left]);
left++;
cur++;
}
else if (a[cur] > key)
{
Swap(&a[cur], &a[right]);
right--;
}
else
{
cur++;
}
}
//[begin,left-1][left,right][right+1,end]
QuickSort(a, begin, left-1);
QuickSort(a, right + 1, end);
}
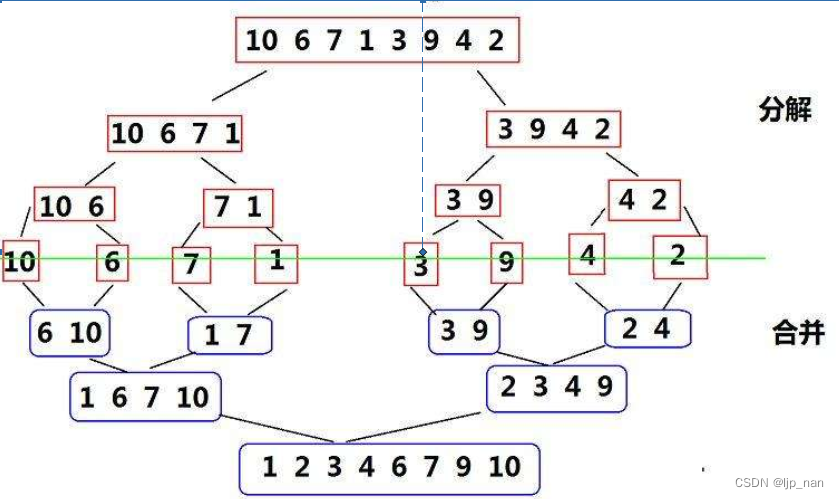
归并排序的递归
基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
递归代码如下所示:
void _MergeSort(int* a, int begin, int end, int* temp)
{
//递归结束条件
if (begin >= end)
{
return;
}
//我们需要分区间进行,把区间可以分为
//[begin,mid][mid+1,end]
int mid = (begin + end) / 2;
//通过后序遍历使得最小的区间有序[0,0][1,1][2,2]……[end-1,end-1][end,end]
_MergeSort(a, begin, mid, temp);
_MergeSort(a, mid+1, end, temp);
//开始处理归并排序,也就是处理二叉树根的排序问题 左右根
//这里相当于合并两个有序数组
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1<=end1&&begin2<=end2)
{
if (a[begin1] < a[begin2])
{
temp[i++] = a[begin1++];
}
else
{
temp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[i++] = a[begin2++];
}
//再把数据拷回去
memcpy(a+begin, temp+begin,sizeof(int)*(end-begin+1));
}
//归并排序递归算法
void MergeSort(int* a, int n)
{
//我们需要开辟一个数组
int* temp = (int*)malloc(sizeof(int) * n);
//进行递归需要一个子函数
_MergeSort(a, 0, n - 1, temp);
free(temp);
}
递归展开图:
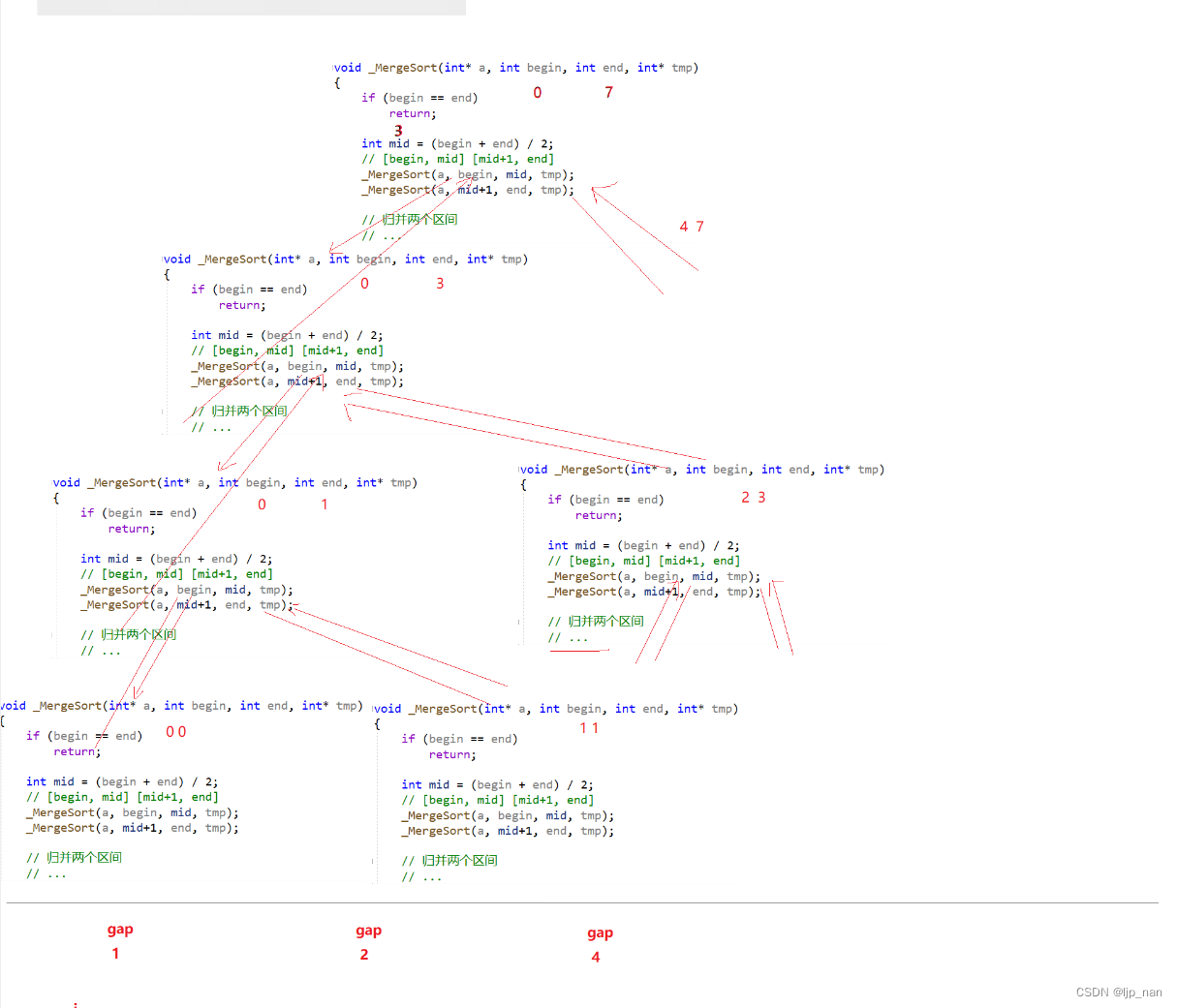
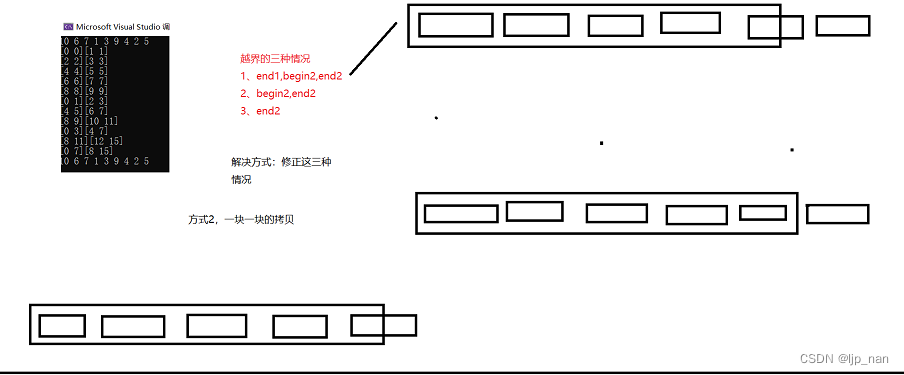
归并排序的非递归
原理:如下图所示:
划分为一个数一个数一组归并排序后再划分为两个数一组,然后再归并直至数组有序
代码如下:
//归并排序非递归
void MergeSortNonS(int* a, int n)
{
int gap = 1;
int* temp = (int*)malloc(sizeof(int) * n);
while (gap < n)
{
int j = 0;
for (int i = 0; i < n; i += gap * 2)
{
//第一趟归并排序1数据归并成两个数,
//第二趟2个数归为4个数
//第三趟4个数,4和4归并成8个数
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + gap * 2 - 1;
//一块一块进行拷贝
/*if (end1 >= n || begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}*/
//直接修正
if (end1 >= n)
{
end1 = n - 1;
//不存在的区间
begin2 = n;
end2 = n-1;
}
else if (end2 >= n)
{
end2 = n - 1;
}
else if (begin2 >= n )
{
begin2 = n;
end2 = n - 1;
}
printf("[%d %d][%d %d]\n", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
temp[j++] = a[begin1++];
}
else
{
temp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
temp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
temp[j++] = a[begin2++];
}
//一块一块进行拷贝
//memcpy(a+i, temp+i, sizeof(int)*(end2-i)+1);
}
//直接拷贝
memcpy(a, temp, sizeof(int) * n);
gap *= 2;
}
free(temp);
}
这里需要注意溢出的三种情况
消除溢出的方法有两种,均已在代码注释中标出。
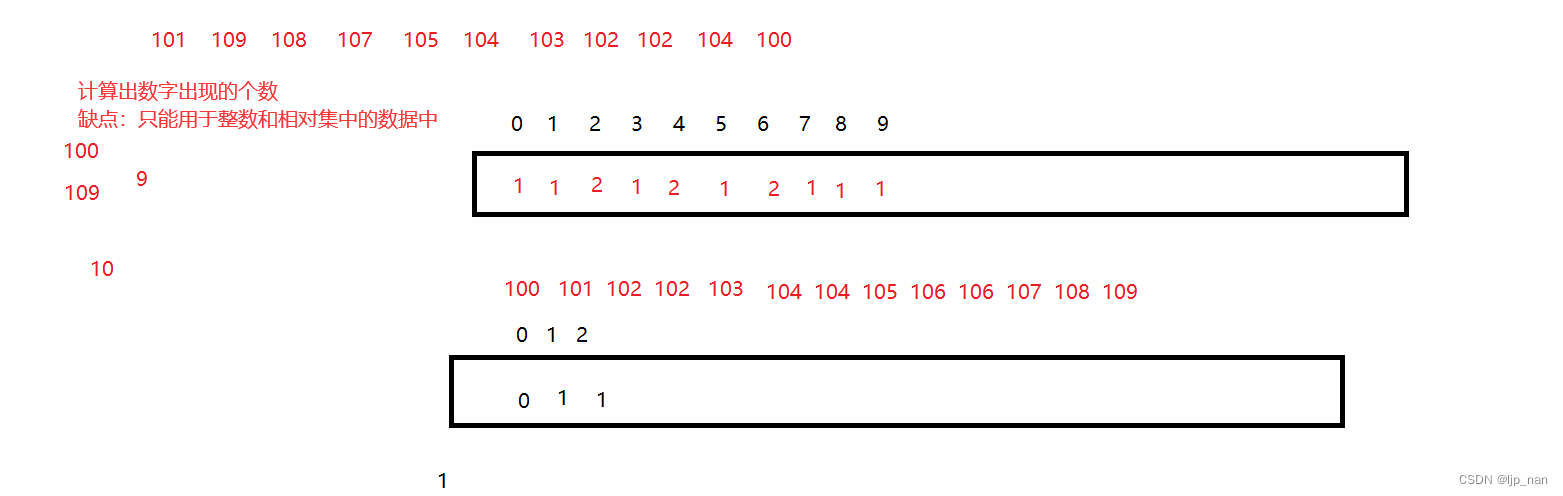
计数排序
计数排序应用了相对映射的方法
如下图所示:
代码实现:
//计数排序
void CountSort(int* a, int n)
{
//首先找出最大值和最小值
int max = a[0];
int min = a[0];
//相对映射
for (int i = 0; i < n; i++)
{
if (max < a[i])
{
max = a[i];
}
if (min > a[i])
{
min = a[i];
}
}
//求出范围
int range = max - min;
//开辟一个range大小的数组
int* temp = (int*)malloc(sizeof(int) * range+1);
for (int i = 0; i < n;i++)
{
temp[i] = 0;
}
//统计次数
for (int i = 0; i < n; i++)
{
temp[a[i] - min]++;
}
//排序
for (int i = 0; i < n; i++)
{
while (temp[i]--)
{
a[i] = i + min;
}
}
free(temp);
}
稳定性
稳定的排序算法:冒泡排序,计数排序,归并排序,直接插入排序。
不稳定的排序算法 :堆排序,快速排序,选择排序,希尔排序。
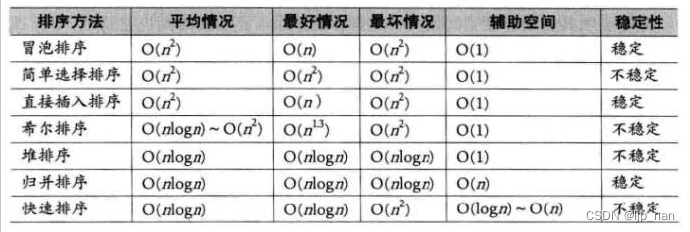
排序算法的时间复杂度
基数排序
时间复杂度O(N+范围)
空间复杂度O(范围)
数据结构的初阶到此为止,高阶数据结构将用C++来描述。