474.一和零

• 本题属于 装满背包最多能有多少个物品 类型
• 本题是容量有两个维度的背包，背包容量是m和n。物品的重量也是两个维度，对应上了背包的容量。
• 本题也属于找最大值的问题，找最大值和基础01背包的找最大价值一样，都是和自身对比找出历史最大值。

给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1：

输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：

输入：strs = ["10", "0", "1"], m = 1, n = 1
输出：2
解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

提示：

• 1 <= strs.length <= 600
• 1 <= strs[i].length <= 100
• strs[i] 仅由 ‘0’ 和 ‘1’ 组成
• 1 <= m, n <= 100

思路

本题题意是数组str里面找长度最大的子集，这个子集需要满足子集里面一共有m个0和n个1.

本题的背包思路是，我们可以把子集里需要的m个0和n个1，想象成一种容器，那么这个问题，就转变成了：

装满m个0 n个1的容器，最多可以有多少个元素（物品）。也就是说，本题不同于前面的情况，属于问装满背包最多有多少个物品类型的题目。

（494.目标和 属于装满背包最多有多少个方案，416.分割等和子集 属于能否装满背包，1049.最后一块石头重量 属于背包最多能装多少）

为什么不是多重背包而是01背包

本题因为是m个0，n个1，因此可能第一反应会是多重背包。

几种背包之间的关系：

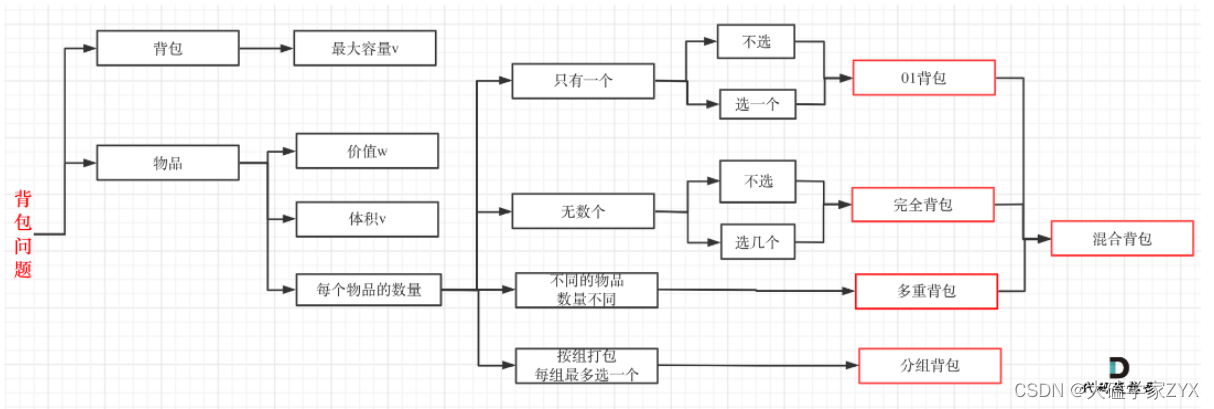
多重背包是每个物品，数量不同的情况。01背包是每个物品只有一个（只能用一次），完全背包是每个物品有无限个。

而本题中，strs 数组里的元素就是物品，每个物品都是一个！也可以理解为因为是选择子集，所以每个物品只能用一次。

而m 和 n相当于是一个背包，并不是属于两个背包，只是一个2维度的背包！

这里要注意，m和n是容量，不是物品，也就意味着m和n代表的是背包。加上本质上选子集还是每个物品只能用一次，所以是01背包问题。

（理解成多重背包主要是把m和n混淆为物品了，感觉这是不同数量的物品，所以以为是多重背包。但是实际上多重背包是限制物品个数，而不是限制背包）

本题01背包，背包有两个维度，一个是m 一个是n，而不同长度的字符串就是不同大小的待装物品。

与之前01背包问题的区别

之前几道01背包问题，是给出容器容量，问装满容器的最大价值（价值=重量的时候就是最大重量）

是多少/能不能装满背包/背包尽量装最多能装多少/装满背包一共多少种方案。

但是本题是01背包的两个维度，是求背包装满的时候最多有多少个物品。

DP数组的含义

我们需要装满一个 容量为m个0，n个1的背包，问背包里最多有多少个物品。

背包有两个维度，所以我们需要定义一个二维DP数组，因为一维DP数组无法表现出背包的两个维度。

二维DP数组dp[i][j]表示，容量为i个0，j个1的背包，最多有dp[i][j]个物品。（也就是装满i个0，j个1的背包，最多有dp个物品）

递推公式（也是求最大值）

01背包递推公式：

dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);

本题的物品也就是str数组里面的元素，例如["10", "0001", "111001", "1", "0"]里的"0001"就是一个物品，这个物品的重量是x个0，y个1。背包的最大重量是m个0，n个1。

因此我们放入每个物品的状态，就是dp[i-x][j-y]。

由于dp[i][j]表示的是容量为{i，j}的背包最多能放的物品个数，因此这个物品放进来之后，物品个数现在的状态是：dp[i-x][j-y]+1，意味着背包能放的容量减少，但是背包物品个数+1。

（DP数组数值本来代表的就是物品个数，下标代表容量）

我们要取的是物品个数的最大值，因此还需要和自身进行对比，存下来历史最大值。（和494.分割等和子集差不多，都是取最大）

因此本题递推公式为：

dp[i][j]=max(dp[i][j],dp[i-x][j-y]+1);//其中x是元素中0的个数，y是元素中1的个数（物品本身重量属性）

初始化

找最大值问题一般初始化都是0，但是要注意dp[0][0]的情况。

dp[0][0]是容量为{0,0}的时候，能装的物品个数就是0。非零下标也全部初始成0，防止求最大值过程被覆盖。

（dp[i][j]表示物品个数，最小就是0）

遍历顺序

遍历顺序也是01背包的遍历顺序。

完整版

• 注意二维背包内层for循环倒序遍历的方式，二维背包的倒序遍历和一维背包倒序类似，但是都要注意下标越界的问题
• 背包倒序遍历的for边界值问题，可以先都写成i>=0和j>=0，后面写完了递推公式再修改

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        //建立二维DP数组存放物品个数dp，下标m是0 n是1
        vector<vector<int>>dp(m+1,vector<int>(n+1,0));//二维数组，最开始手误写成了一维
        
        //对于strs里面每个数字，找重量属性,这已经属于遍历物品了
        for(int i=0;i<strs.size();i++){
            int zeroNum = 0;
        	int oneNum = 0;
            for(int j=0;j<strs[i].size();j++){//注意字符串本身就是一个数组，一维字符数组等于一个二维int数组
                if(strs[i][j]=='0') zeroNum++;
                else oneNum++;
            }
            //统计完物品的重量，再进行dp递推,物品已经在外层遍历，直接开始背包容量倒序遍历
            for(int i=m;i>=zeroNum;i--){
                for(int j=n;j>=oneNum;j--){
                    dp[i][j]=max(dp[i][j],dp[i-zeroNum][j-oneNum]+1);
                }
            }
        }
		return dp[m][n];
    }
};

总结

01背包问题不同维度的应用：

• 纯 0 - 1 背包 是求 给定背包容量，背包的最大价值是多少。
• 416. 分割等和子集 是求 给定背包容量，能不能装满这个背包。
• 1049. 最后一块石头的重量 II 是求 给定背包容量，尽可能装，最多能装多少。
• 494. 目标和 是求 给定背包容量，装满背包一共有多少种方案。
• 474.一和零 是求 给定背包容量，装满背包最多有多少个物品。（本题属于二维容量的背包）