跳跃游戏 Ⅰ

① 任务描述：

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度，判断你是否能够到达最后一个下标。

本题取自 leetcode 面试150题题集

> 示例一

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

解释：根据题目可知，每个节点最多可跳 nums[i] 步，那么在i点时，最大可达位置为 i + nums[i]，可以通过贪心算法，比较 maxStep 当前最大可达位置和当前最大可达步数大小： maxStep = Math.max(maxStep, i + nums[i])，具体效果可以参考下图：

效果图

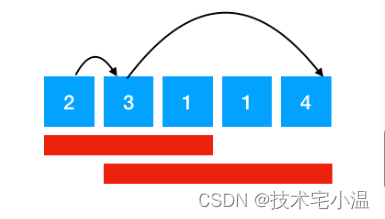
如上图所示，第 2 个位置的最大可达位置已经大于等于目的地的位置下标了，故可达目的地！

> 示例二

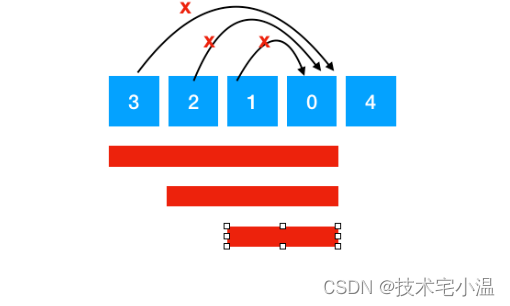
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

解释：如下图所示：无论哪个节点，可达的最大位置均小于目的地的下标，故不能到达目的地！

在这里插入图片描述

② 题意解析

根据题目，可知：题目需要计算出一组数据中，能否到达目标位置，故我们需要求数据中，在能抵达的情况下，求得最大可达位置，并且与目标位置下标进行比较。若最大可达位置 > 目标下标，则可达目的地，返回 true，反之返回 false。

解题思路
通过循环一步一步去获取每一步的最大可跳跃到达的位置，与上一步最大可达位置比较大小，取最大值！需要规定前提是，上一步的最大可达位置大于当前位置下标，否则为到达不了！

③ 解决方案：

/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canJump = function(nums) {
	// 写法一： 仅为了展示每个点可达的最大距离
    let numsInfo = nums.reduce((pre, cur, curIndex) => {
        // 这个是为了展示每个节点最远可达距离，取每个点最远可达距离，一个一个向前递进
        pre.itemLenList.push([curIndex, curIndex + cur])

        if(curIndex !== nums.length - 1 && pre.maxStep >= curIndex) {
            // 获取全局最远可达距离，其实可以用循环代替，当最远可达距离超出或抵达目标点，就可以退出了，用这种主要为了理解
            pre.maxStep = Math.max(pre.maxStep, curIndex + cur)
        }
        return pre
    }, { itemLenList: [], maxStep: 0 })

    return numsInfo.maxStep >= nums.length - 1
	
	// 语义化写法二：
	// 默认第一步自执行，即初始赋值为nums[0]
    let len = nums.length, maxStep = nums[0]
    for(let i = 1; i < len - 1; i++) {
    	// 判断提前到达，结束循环
        if(maxStep >= len - 1) break
        
        // 判断上一个最大可达位置是否能到达当前下标，能则继续，反之结束循环
        if(maxStep >= i) {
            maxStep = Math.max(maxStep, i + nums[i])
        }  else break
    }

    return maxStep >= len - 1
};

跳跃游戏 Ⅱ

① 任务描述：

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

提示：

1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]

> 示例一

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

> 示例二

输入: nums = [2,3,0,1,4]
输出: 2

② 题意解析

根据题目可知，这组 nums数据，是必定能够到达 nums[n - 1]。只需要求到达目的的最优解，最少步数。说到步数，自然要与贪心算法联系起来，这题也不例外！我们需要在尽量减少步数的情况下，走最大可达位置。

这就需要我们记录当前节点对应的最大可达位置，这与上一题相似，通过 Math.max() 循环取最值。在循环到上一个节点最大可达位置时，将走到这个位置途径的节点中最大值进行赋值。相当于更新最大可达到位置，使循环继续前进！直到当最大可达位置到达目的地！

每当最大可达位置没到目标位置，但又到达了当前循环节点下标 i 时，记录为一次跳跃，即：向前跳跃一步！计入步数中。

效果图

如上图所示，当 下标 0 的可达最大位置，与 i 循环到 2时（lastMaxIndex === i），已经无法继续前进时，需要选择一个 lastMaxIndex 步数内能到达最远的一个位置去跳跃，也就是下图中的 下标 1 的位置，为上一个节点 lastMaxIndex 内，最远可达的节点，故将它更新赋值给 lastMaxIndex 。此时判断是否满足条件，不满足则继续循环执行，反之则退出循环，输出结果！

③ 解决方案

/**
 * @param {number[]} nums
 * @return {number}
 */
var jump = function(nums) {
    let len = nums.length
    let lastMaxIndex = 0
    let maxReachIndex = 0
    let steps = 0

    for(let i = 0; i < len - 1; i++) {
        // 获取 lastMaxIndex 途径的最大可达距离
        maxReachIndex = Math.max(maxReachIndex, nums[i] + i)

        // 当lastMaxIndex已经到达目的地，跳出循环
        if(lastMaxIndex >= len - 1) break

        /* 当 i 已经循环到 上一个节点的位置，但却没有退出循环时，此
        时需要寻找下一个可以跳到最远的距离的节点。 即： 将 maxReachIndex 
        途径点取的最大可达距离赋值给 lastMaxIndex，故 maxReachIndex 最大值所
        在的下标为下一个跳跃的节点（不需要记录）。
        */
        if(lastMaxIndex === i) {
            lastMaxIndex = maxReachIndex
            steps++
        }
    }
    return steps
};