山外风雨三尺剑
有事提剑下山去
云中花鸟一屋书
无忧翻书圣贤来
1.设置问题
以Web广告和点击量的关系为例来学习回归。
前提:投入的广告费越多,广告的点击量就越高。
根据以往的经验数据,可以得到下图:

那么假设我要投200块的广告费,那么带来的点击量有多少呢?
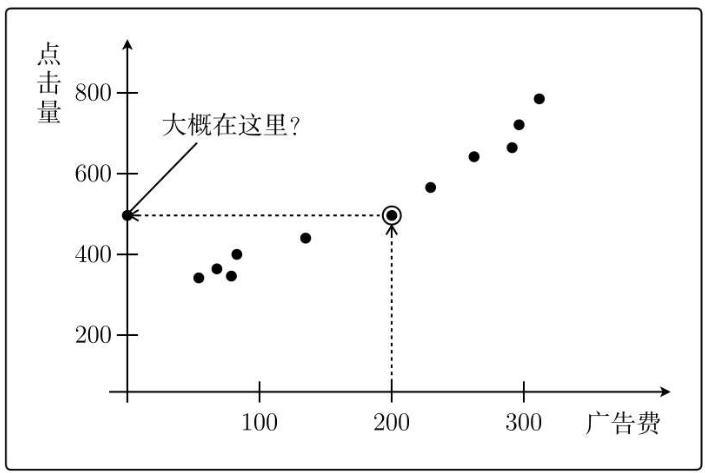
也就是500次左右。
这就是机器学习。你所做的事情正是从已知的数据中进行学习,然后给出预测值。
2.定义模型
只要知道通过图中各点的函数形式,就能根据广告费得知点击量。
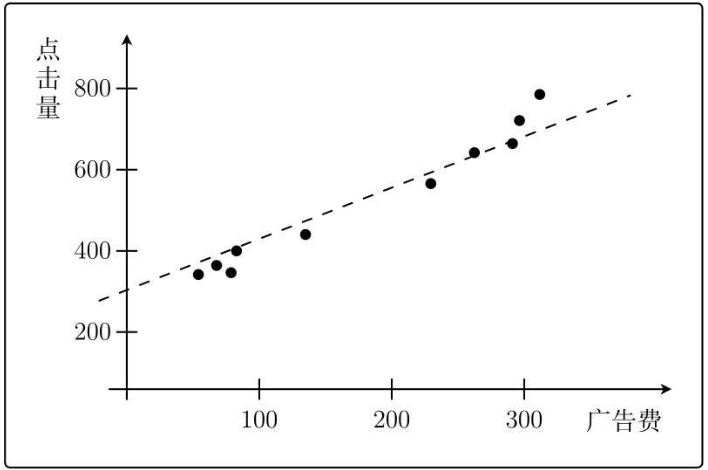
注意:“点击量中含有噪声”,所以函数不可能穿过所有的点。
可以得到一次函数:
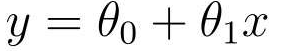
一个是截距,一个表示斜率。
由这个函数可知,x是广告费,y是点击量。
可以把上面这个一次函数想象成是一个能够根据投入广告费预测点击量的模型,而θ0和θ1就是模型的参数值。模型的好坏(即预测结果的准确性)和模型的参数值息息相关。
现在我们不知道这两个参数值取多少对这个模型来说最优。
根据数学中的假设法,既然不知道,就先随便假设试一试。先假设θ0=1、θ1=2,那么上面的一次函数就会变成:

根据假设的这个模型,现在我要投入x=100块钱的广告费,那么预测的点击量:
y = 1 + 2 * 100 =201
再看一下之前数据实际情况:
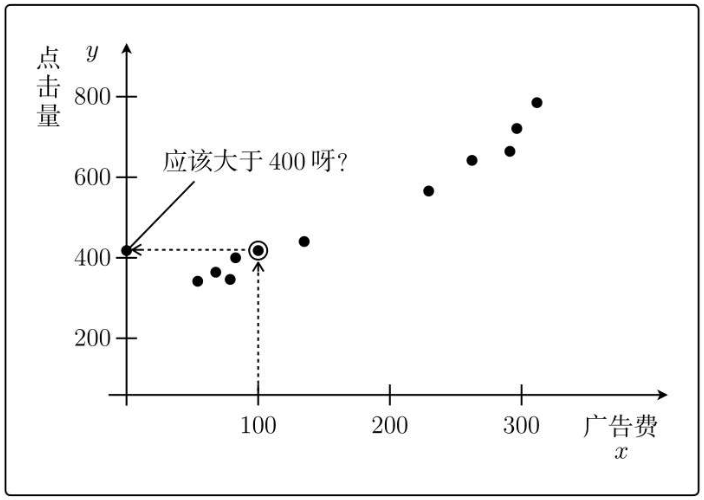
所以假设的θ0=1、θ1=2完全不正确,根据这两个参数得出的模型,并不能得到正确结果。
下面我们就是要使用机器学习来求出正确的θ0与θ1。
3 最小二乘法
首先,转换一次函数的表达式:
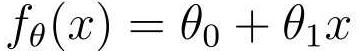
这样就能一眼看出,这是一个含有参数θ,并且和变量x相关的函数。
我们之前有过投入的广告费与点击量之间的实际数据,如下:
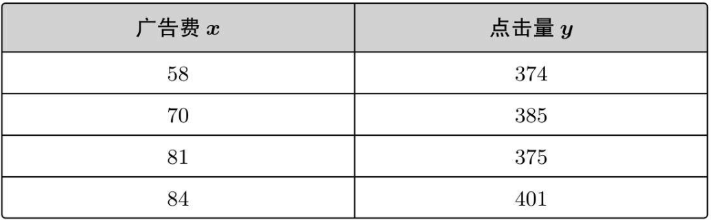
在图中表示:

根据刚才我们随便假设的参数,可以得到 fθ(x)=1+2x
将实际投入的广告费代入预测点击量:
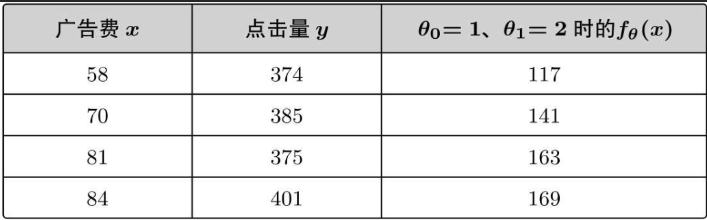
可以看出,根据随便假设的参数预测的值与实际情况相差很大,这种用随便确定的参数计算的值与实际的值存在偏差。
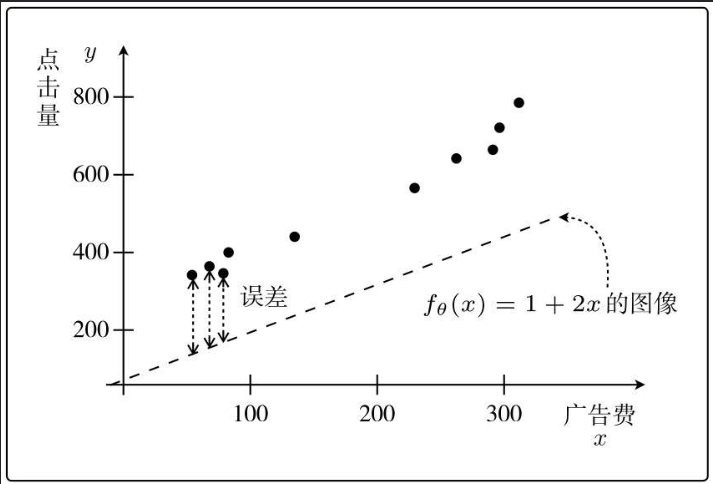
最理想的情况是,我们的预测值与实际值一致,即y-fθ(x)=0。这就是说y和fθ(x)之间的误差为0。
但是,不可能让所有的误差都等于0,所以我们要做的就是让所有点的误差之和尽可能小。
用表达式展现出来就是:

这个表达式称为目标函数(核心),E(θ)的E是误差的英语单词Error的首字母,这类问题叫最优化问题。
注意点:
1. x(i)和y(i)中的i不是i次幂的意思,而是指第i个训练数据。
2. 要计算误差的平方,排除误差为负值的情况。
3. 乘以1/2,表达式更好微分,而且不影响函数本身取最小值的点。
将开始的广告费与点击量数据代入进去可得:
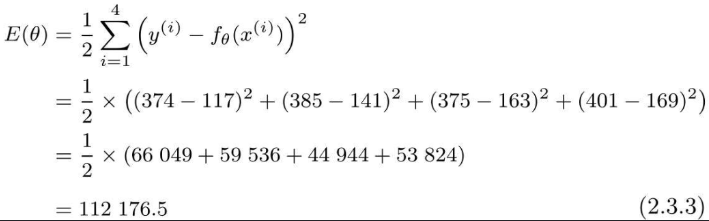
误差太大,我们要做的就是让误差变小,使得预测值接近实际值,这种求误差的方法也叫作最小二乘法。
要让E(θ)越来越小,就要去不停参数θ的值,然后再去与实际值一次次进行比较修改,这样太麻烦,正确做法是使用微分。
示例:
有一个二次函数为g(x)=(x-1)*2

首先对g(x)进行微分:

可以知道它的增减表:

在x=3这一点,为了使g(x)的值变小,我们需要向左移动x,也就是必须减小x

在另一侧的x=-1这一点,为了使g(x)的值变小,我们需要向右移动x,也就是必须增加x
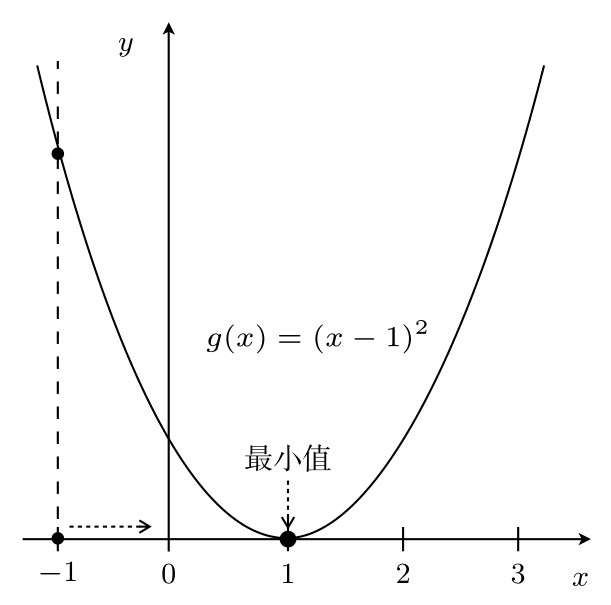
也就是说根据导数的符号来决定移动x的方向,与导数符号相反的方向移动,g(x)就会沿着最小值的方向前进。
把上面说的话总结起来,用表达式来表示:
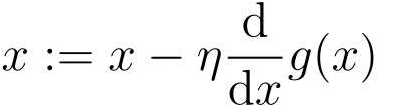
这就是最速下降法或梯度下降法。
A:=B这种写法,它的意思是通过B来定义A,参数自动更新。简单来说,就是用上一个x来定义新的x。
η称为学习率,读作“伊塔”。根据学习率的大小,到达最小值的更新次数也会发生变化。换种说法就是收敛速度会不同。有时候甚至会出现完全无法收敛,一直发散的情况。
所以η的取值很重要,如η=1,从x=3开始

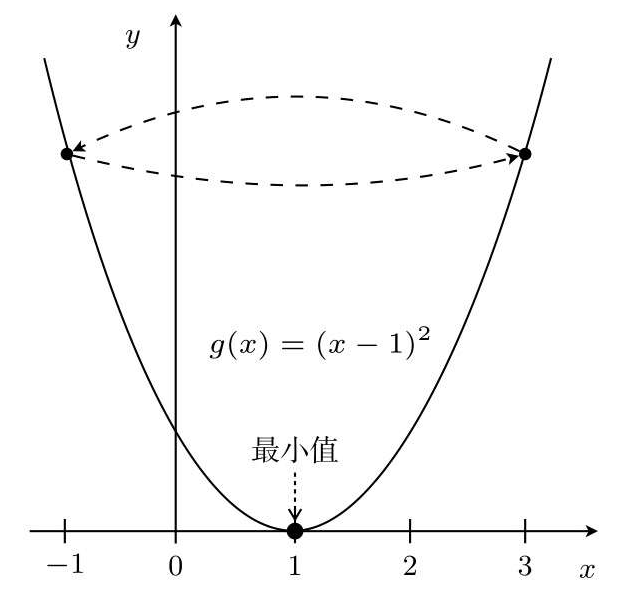
这样就会陷入死循环。
设η=0.1,同样从x=3开始


如果η较大,那么x:=x-η(2x-2)会在两个值上跳来跳去,甚至有可能远离最小值。这就是发散状态。而当η较小时,移动量也变小,更新次数就会增加,但是值确实是会朝着收敛的方向而去。
现在我们再来讨论广告费与点击量的目标函数:
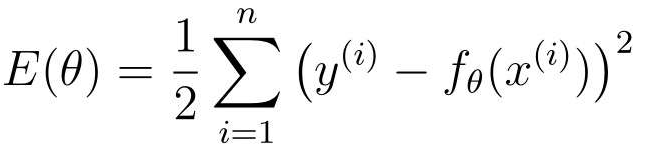
但是这个目标函数中包含fθ(x),fθ(x)拥有θ0和θ1两个参数。也就是说这个目标函数是拥有θ0和θ1的双变量函数,所以不能用普通的微分,而要用偏微分。
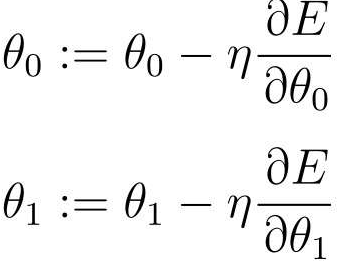
求表达式θ0的偏微分:
E(θ)中有fθ(x),而fθ(x)中又有θ0,所以可以使用复合函数
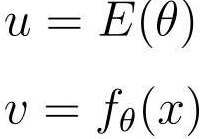
阶梯型地进行微分
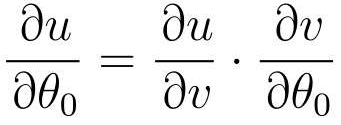
先从u对v微分的地方开始计算
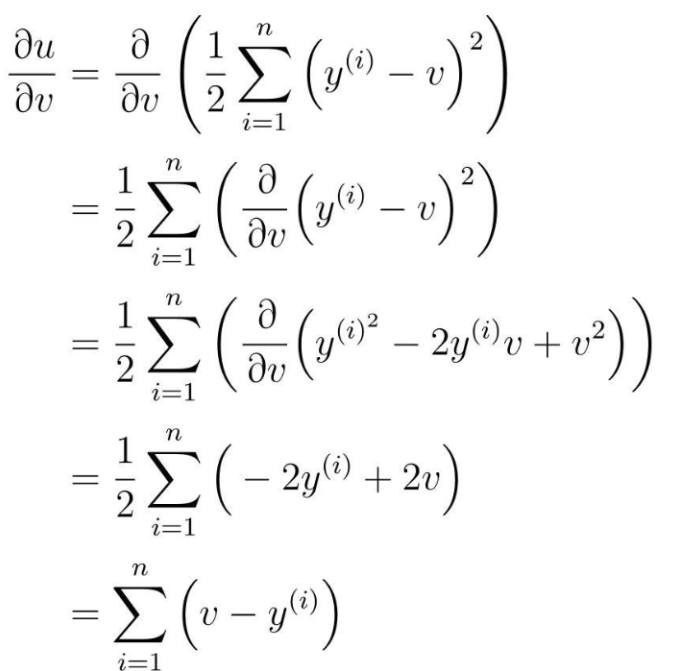
再v对θ0进行微分
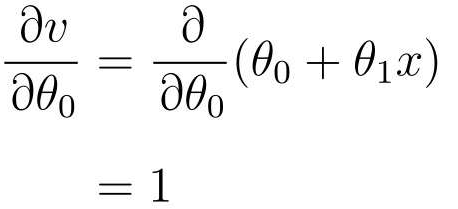
v替换回fθ(x)

再v对θ0进行微分
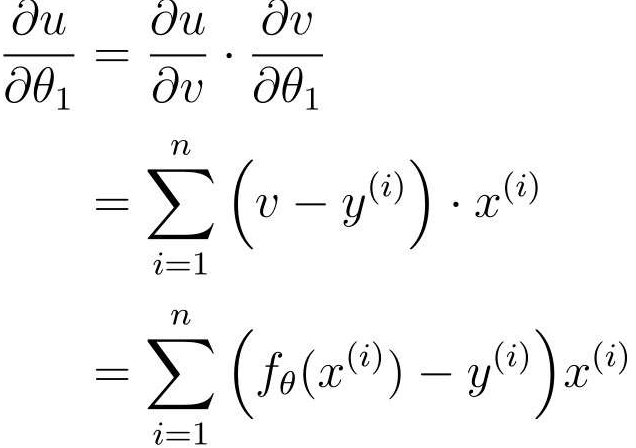
最后得到参数θ0和θ1的更新表达式:

只要根据这个表达式来更新θ0和θ1,就可以找到正确的一次函数fθ(x)了。
用这个方法找到正确的fθ(x),然后输入任意的广告费,就可以得到相应的点击量。这样我们就能根据广告费预测点击量了。
4 多项式回归
之前是将图像拟合成了一条直线,但是,在实际情况中,曲线比直线拟合的效果会更好。

曲线对应的二次函数:
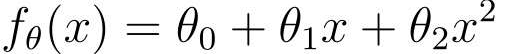
或者使用更大次数的表达式也可以:
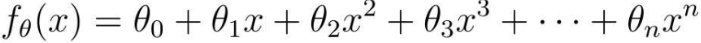
但是,并不是函数次数越好,拟合的就越好,可能会出现过拟合问题。
最终的参数更新表达式:

像这样增加函数中多项式的次数,然后再使用函数的分析方法被称为多项式回归。
5 多重回归
之前我们是根据广告费来预测点击量,即只有一个变量(广告费x),但是在实际中要解决的很多问题是变量超过两个的复杂问题。
比如,除了广告费,点击量的多少还受到广告展示位置和广告版面大小等多个要素,即多个变量x。
为了让问题尽可能地简单,这次我们只考虑广告版面的大小,设广告费为x1、广告栏的宽为x2、广告栏的高为x3,那么fθ可以表示如下:

然后就可以对函数做微分了,但是在这之前可以了解一下表达式的简化形式。
简化方法:把参数θ和变量x看做向量

为了方便计算,两边对齐
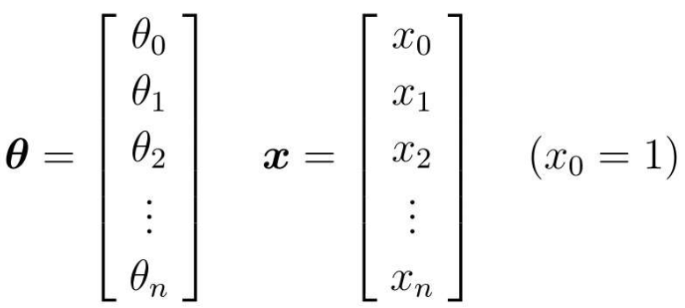
把θ转置之后,与x相乘的结果
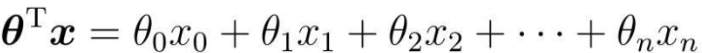
所以,在实际编程时,只需要用普通的一维数组表示就可以:

求微分时是与之前一样的,所以只需要求v对θj的微分就好了

那么第j个参数的更新表达式:
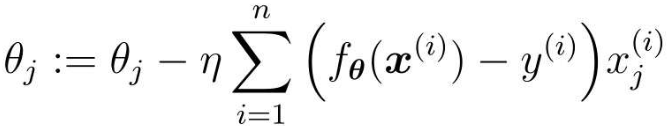
这样包含多个变量的回归称为多重回归。
6 随机梯度下降法
前面讲的梯度下降算法有两个缺点,一个是一次次更新x,花费的时间长,还有就是容易陷入局部最优解。
比如下面这种函数:
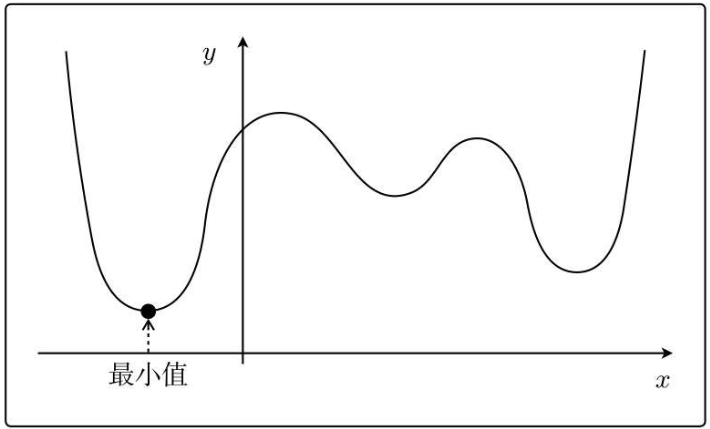
从不同地方选择最开始的x,会陷入局部最优解。
随机梯度下降法是以最速下降法为基础的。
最速下降法的参数更新表达式:
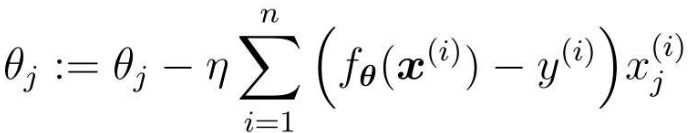
这个表达式使用了所有训练数据的误差。而在随机梯度下降法中会随机选择一个训练数据,并使用它来更新参数。

表达式中的k就是被随机选中的数据索引。最速下降法更新1次参数的时间,随机梯度下降法可以更新n次。此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部最优解。
此外还有随机选择m个训练数据来更新参数的做法:
设随机选择m个训练数据的索引的集合为K
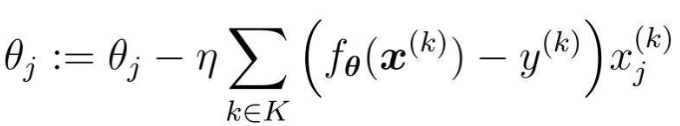
假设训练数据有100个,那么在m=10时,创建一个有10个随机数的索引的集合,例如K={61, 53, 59, 16, 30, 21, 85,31, 51, 10},然后重复更新参数就行了。
这种方法叫做小批量梯度下降法。