我们计算几何概率时，会很容易发现这么一个特点

我们很容易计算

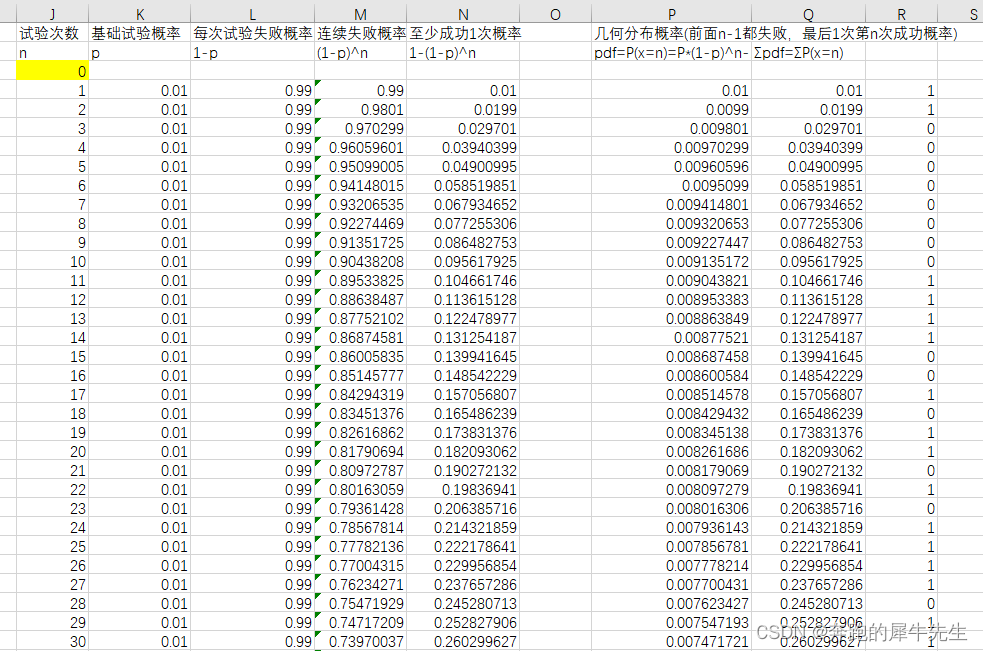
• 试验n次，连续成功概率
• 试验n次，连续失败概率
• 试验n次，至少成功1次概率
• 试验n次，最后一次成功概率
• 试验n次，成功k次概率
• 试验n次，累计成功k次概率

 

2  推导

• 试验n次, p是单次试验的成功概率
• P(至少成功1次概率) =Σp(几何分布概率之和)

• P(至少成功1次概率)
• =1-P(连续失败的概率)
• =1-p(失败)*p(失败)*....*p(失败)
• =1-(1-p)^n

• =Σp(几何分布概率之和)
• =p*p(失败)^0+p*p(失败)^1+p*p(失败)^2+p*p(失败)^3+....+p*p(失败)^(n-1)
• =p*(1-p)^0+p*(1-p)^1+p*(1-p)^2+p*(1-p)^3+....+p*(1-p)^(n-1)
• =p*((1-p)^0+(1-p)^1+(1-p)^2+(1-p)^3+....+(1-p)^(n-1))
• 因为后面是等比数列，而且从0到n-1就是n个
• =p*(1-(1-p)^n)/(1-(1-p)))     
• =p*(1-(1-p)^n)/(1-(1-p)))   
• =p*(1-(1-p)^n)/p
• =1-(1-p)^n

• P(至少成功1次概率)=Σp(几何分布概率之和)=1-(1-p)^n

3  原理

4  技巧