二、无穷小量与无穷大量

概念

在数学中，无穷小量和无穷大量是描述数值趋近于无穷或趋近于零的概念。它们在微积分和数学分析中起着重要的作用。

无穷小量指的是在某一限定条件下，趋近于零的量。它通常用符号"dx"、"dy"或"dt"等表示，表示一个非常接近于零的数。无穷小量在微积分中用于描述函数的局部变化率，也用于表示微分和积分的基本概念。

无穷大量则是指趋近于无穷大的量。它通常用符号"∞"表示，表示一个比任何有限数都要大的数。无穷大量在数学分析中用于描述函数在某些点或趋近于某些点时的趋势和行为。无穷大量可以分为正无穷大和负无穷大，分别表示趋近于正无穷和负无穷。

在微积分中，无穷小量和无穷大量是密切相关的概念。例如，当一个函数的自变量趋近于某个值时，函数的增量可以用无穷小量来表示，而当自变量趋近于无穷时，函数的极限可以用无穷大量来表示。

无穷小量和无穷大量的概念在微积分的推导和证明中经常被使用。它们可以帮助我们研究函数的性质、计算极限、求导和积分等。通过使用无穷小量和无穷大量的概念，我们可以更加精确地描述和分析数学问题，推动数学理论的发展和应用。
在微积分中，无穷小量和无穷大量是描述变量接近无穷大或无穷小的概念。

---

（1）无穷小的概念

（2）无穷小的性质

---

无穷个无穷小的和不是无穷小-证明

---

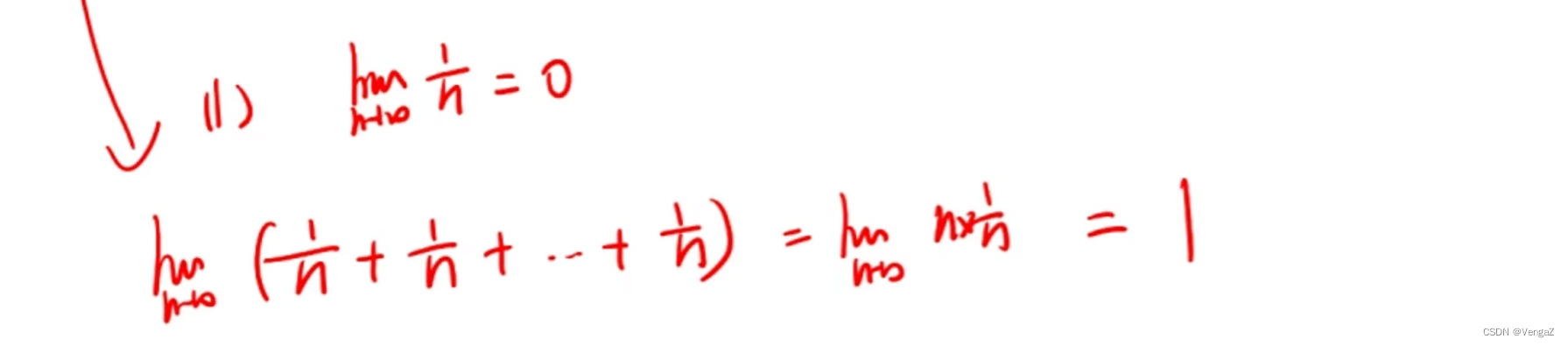
无穷个无穷小量的乘积不是无穷小-证明（没看懂）

---

无穷小量与有界量的乘积仍是无穷小-证明

---

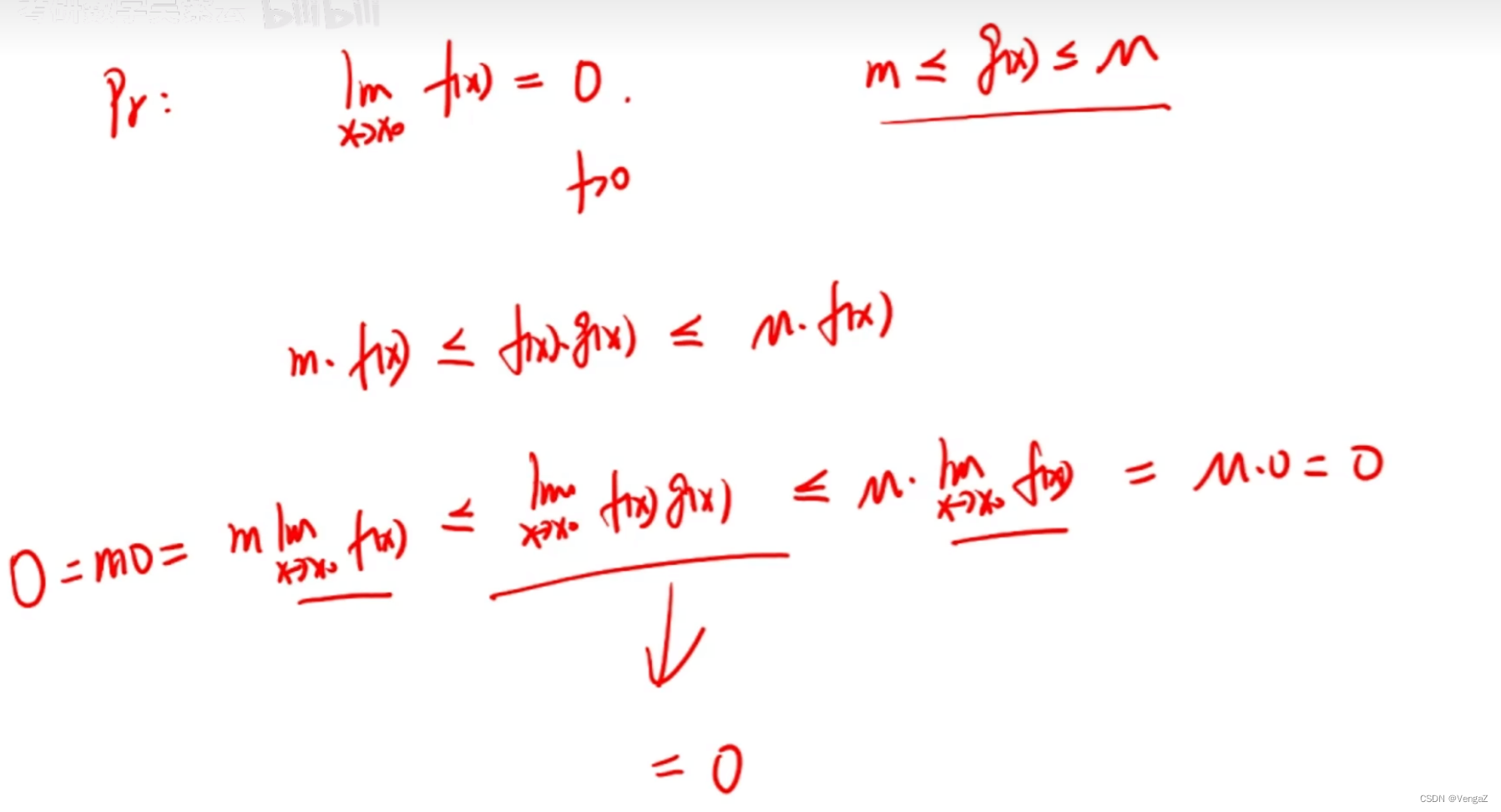
（3）无穷小的比较

常用的等价替换（***）

【高等数学】等价无穷小代换

例23

极限值与无穷小之间的关系（极限脱号）

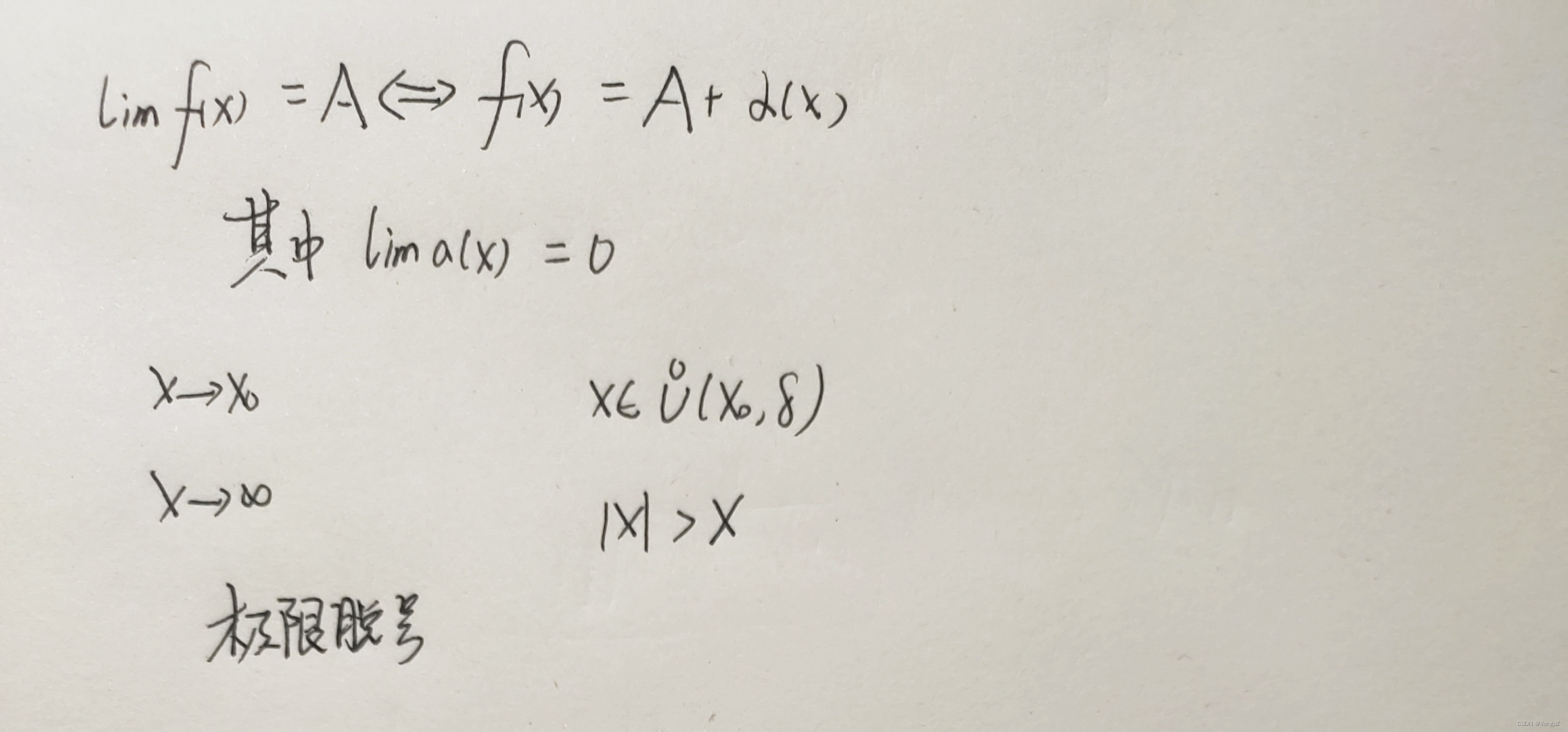
例25

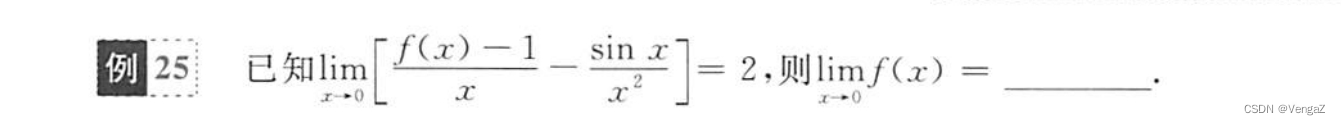
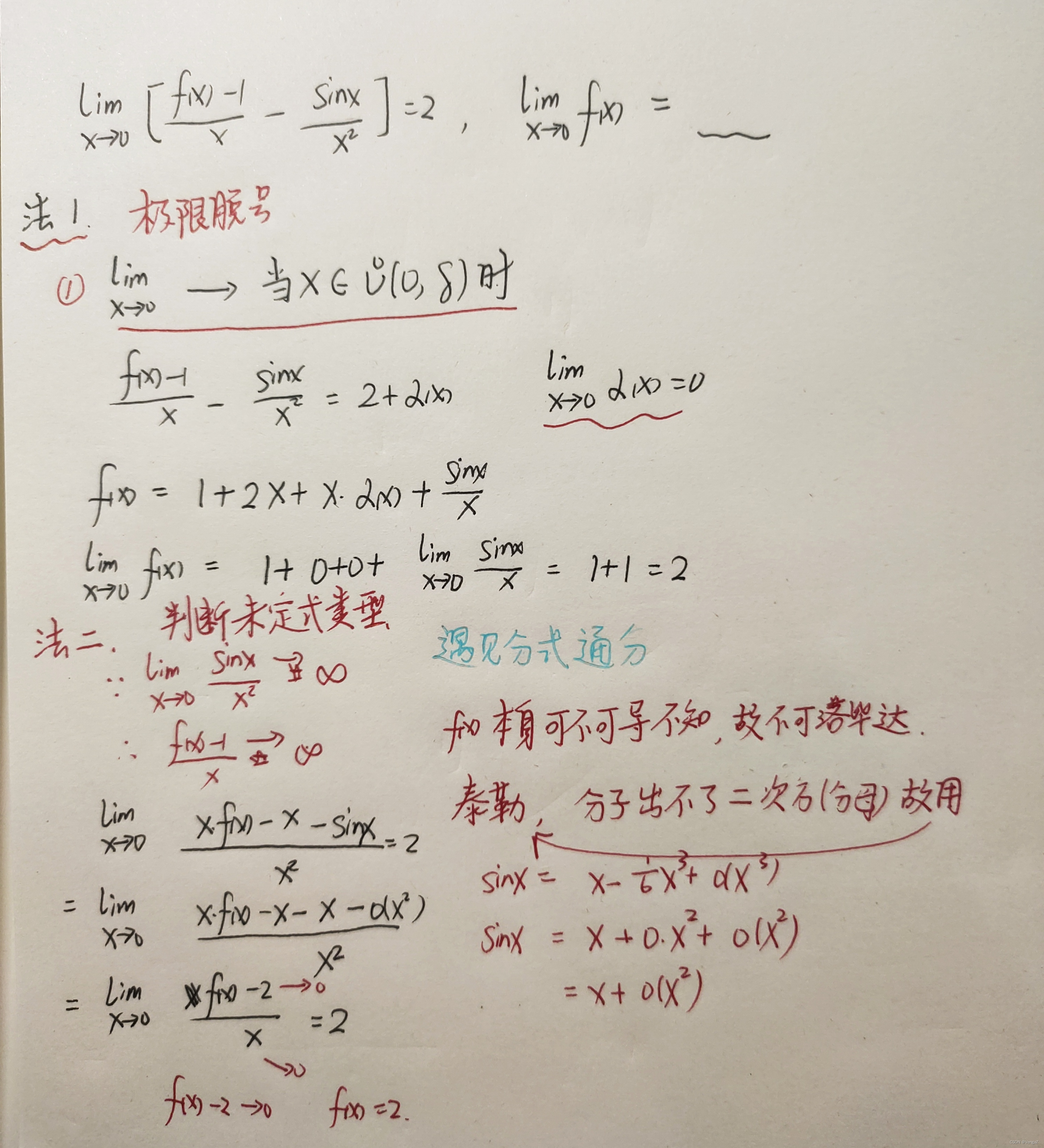
（4）无穷大量

无穷大量的概念

无穷大量的性质

常用的一些无穷大量的比较（抓大头）

无穷大量与无界变量的关系

例30

经典无界不为无穷

无穷大量与无穷小量的关系

总结

无穷小量（Infinitesimal）是指当变量趋近某个极限值时，其取值无限接近于零但不等于零的量。在数学符号中，通常用Δx或dx表示无穷小量。

无穷大量（Infinity）是指当变量趋近某个极限值时，其取值无限接近于无穷大的量。在数学符号中，通常用∞表示无穷大量。

这两个概念常常在极限理论和微积分中使用。例如，在计算函数的导数时，我们可以利用无穷小量的概念来描述函数在某一点的瞬时变化率。而在计算极限时，我们可以利用无穷大量的概念来描述函数在无穷远处的趋势。

需要注意的是，无穷小量和无穷大量并不是实数范围内的数值，它们是一种数学上的概念。在实际应用中，我们通常使用极限的方法来处理这些概念，而不直接涉及无穷小量和无穷大量。

总结起来，无穷小量表示变量趋近于零但不等于零的量，而无穷大量表示变量趋近于无穷大的量。它们在微积分中被广泛应用，用于描述函数的变化和极限的概念。