博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译：https://yalmip.github.io/tutorials/

1.决策变量的定义

1.1 sdpvar

上文简单介绍了sdpvar函数的用法，接下来将对其进行详细介绍。复习一下，sdpvar函数的基本语法如下：

x = sdpvar(n)

x = sdpvar(n,m)

x = sdpvar(n,m,'type')

x = sdpvar(n,m,'type','field')

x = sdpvar(dim1,dim2,dim3,...,dimn,'type','field')

sdpvar x

1.1.1）x = sdpvar(n)

        该命令用于定义一个n阶的对称变量方阵，当n=1时，也就相当于定义一个标量；

1.1.2）x = sdpvar(n,m)

        该命令用于定义一个n行m列的变量矩阵，当n=m时，默认该变量矩阵具有对称性，也就是说，如果使用sdpvar定义了方阵x，则x(i,j) = x(j,i)，例如，定义一个3行3列决策变量P的语法如下：

P = sdpvar(3,3);

        这时候变量P默认为一个对称矩阵，也就是P(1,2) = P(2,1)，P(1,3) = P(3,1)，P(2,3) = P(3,2)。

1.1.3）x = sdpvar(n,m,'type')

        sdpvar函数的第三个参数用于初始化变量的性质，例如需要定义一个不对称的变量P，则需要将第三个参数设置为'full'，语法如下：

P = sdpvar(3,3,'full');

在定义n阶变量方阵时，其他可使用的'type'参数如表1所示：

表1 sdpvar函数中常用的'type'参数

'type'参数	简化表示	含义
'full'	'f'	完整的不对称变量矩阵
'symmetric'	'sy'	对称变量矩阵
'diagonal'	/	对角阵
'toeplitz'	't'	对称托普利茨矩阵
'hankel'	/	非对称hankel矩阵
'rhankel'	/	对称hankel矩阵
'skew'	'sk'	反对称矩阵
'Hermitian'	/	hermitian矩阵

1.1.4）x = sdpvar(n,m,'type','field')

        sdpvar函数中的第四个参数'field'可用于定义复数变量矩阵。不输入任何参数时默认是实数变量矩阵，当需要定义复数矩阵时，可以添加参数'complex'，形式如下：

P = sdpvar(3,3,'full','complex');

        上面的语句就表示定义了一个3阶不对称的复数变量方阵。

1.1.5）sdpvar x

        该语句表示定义一个标量x（也可以理解为1行1列的变量），也可以同时定义多个标量，语句如下：

sdpvar a b c d e

        上述语句就表示定义了5个不同的标量a,b,c,d,e。

        综上，在Yalmip工具箱中一共有三种不同的方式定义标量，分别如下：

a = sdpvar(1);

a = sdpvar(1,1);

sdpvar a

        三个语句的作用完全一样，可以按照自身的使用习惯进行选择。对于二维变量，也可以通过这种方式进行定义，但根据官方文档所述，这种方式可能存在bug，建议谨慎使用：

sdpvar a(2,2);

        上述代码表示定义一个2行2列的变量a。

1.1.6）定义多维变量（三维及以上）

        对于三维以上的变量，Yalmip工具箱可以有两种不同的建模方式（当然还有简单的一种，将多维变量转为低维变量，例如2×3×4的三维变量可以转为2×12的二维变量，也可以转为1×24的一维变量，这里不再赘述），元胞数组和多维sdpvar对象，两种建模方式分别如下：

        ①定义元胞类型(cell)的sdpvar变量

        假设需要定义一个5×20×80的变量M，使用cell定义的方法为：

M = cell(1,5);

for k = 1:5

  M{k} = sdpvar(20,80);

end

也可以写成：

M = sdpvar(20*ones(5,1),80*ones(5,1));

        两种定义方式是等价的。

 

        使用cell格式定义多维变量比较方便，但缺点是无法使用一些常用的数学运算函数，例如下面的代码将会报错：

M = sdpvar(20*ones(5,1),80*ones(5,1));

N = sdpvar(20*ones(5,1),80*ones(5,1));

M + N

 

        更高维度的变量也可以采用相同的方式进行定义，例如下面的代码就是定义了一个5×5×10×20的变量L：

L = sdpvar(5,5,10,20);

        需要主义的是，因为变量L前两个维度是相同的，按照之前的说明，前两个维度始终是对称的，为了定义一个不对称的变量L，也需要添加参数'full'：

L = sdpvar(5,5,10,20,'full');

        这样就可以保证L的前两个维度不是对称的。

1.2 binvar

        binvar和sdpvar的语法完全一样，唯一不同的就是使用binvar定义的变量是0-1变量，也就是取值要么为0，要么为1。在实际的优化问题中很多变量都可以建模为0-1变量，例如仓库选址、配电网的支路状态等。同时，对于约束条件中的逻辑“或”的关系，也可以通过0-1变量进行建模（这实际上是线性规划的知识，我在这里只做简单介绍）。下面举两个例子：

例1：

变量x，y满足：4x + 3y ≤ 50  (1) 或x + y ≤ 20  (2)

        对于例1的约束条件，可以通过引入一个0-1变量w和一个足够大的正数M进行建模(实际上这就是常说的大M法)，建模方式如下：

sdpvar x y

binvar w

M = 1e5;

Constraints = [4*x + 3*y - 50 <= w*M , x + y -20 <= (1-w)*M];

        当w=1时，约束1成立，当w=0时，约束2成立，这样就通过0-1变量完成了约束条件中逻辑“或”的表达。

例2：

变量x，y满足下面3个不等式其中2个：

4x + 3y ≤ 50，x + y ≤ 20，3x+2y <= 35

        对于例2的约束条件，可以通过引入一个3维0-1变量w和一个足够大的正数M进行建模，建模方式如下：

sdpvar x y

w = binvar(1,3);

M = 1e5;

Constraints = [

    4*x + 3*y - 50 <= w(1)*M ,...

    x + y -20 <= w(2)*M , ...

    3*x +2*y -35 <= w(3)*M , ...

    sum(w) == 2];

        当w1=1时，约束1成立，当w2=1时，约束2成立，当w3=1时，约束3成立，同时令w1+w2+w3=2，这样就通过0-1变量完成了3个约束条件中必须满足其中2个的表达。

        通过0-1变量，还可以实现分段函数、分类讨论等表达，此处不再赘述。

        另外，也可以先把变量定义为连续型，然后通过binary函数约束为0-1变量，具体用法如下：

x = sdpvar(2,3);

Constraints = [binary(x)];

1.3 intvar

        intvar和sdpvar的语法完全一样，唯一不同的就是使用intvar定义的变量是整数变量，也就是取值只能为整数。在实际的优化问题中很多变量都可以建模为整数变量，例如人数、商品件数等。

1.4 semivar

        semivar和sdpvar的语法完全一样，唯一不同的就是使用semivar定义的变量是半连续变量，也就是取值要么为0，要么为某个区间内的连续变量。但使用semivar时，可能会出现求解器不支持的情况。按上文的介绍，这种变量可以理解为逻辑“或”的关系，可以通过引入0-1变量使用大M法进行建模。为了避免求解器不支持导致模型无法求解，所以semivar很少使用，通常都会应用大M法对半连续变量进行建模。

2.决策变量相关函数

        在这一节的介绍之前，首先说明一点，sdpvar时Yamlip中的一个函数，用于定义决策变量，定义的决策变量在Matlab中为sdpvar类型。而binvar、intvar等函数定义的决策变量，本质上就是带有约束的sdpvar类型变量。所以，下面介绍的决策变量相关函数适用于所有sdpvar类型的变量，而不仅仅是通过sdpvar函数定义的变量。

2.1常见的数学运算

        Matlab中几乎所有的数学运算都可应用于sdpvar类型的变量，最常用的数学运算函数以及符号如表2所示：

表2 sdpvar类型变量常用的数学运算

数学运算	含义	用法
+	加法	x+y
-	减法	x-y
*	乘法，可用于标量和矩阵相乘以及矩阵乘法	x*y
.*	用于维度相同的矩阵，表示对应元素相乘	x.*y
abs	求绝对值	y = abs(x)
det	求行列式，仅用于方阵	y = det(x)
exp	指数函数	y = exp(x)
floor	向下取整	y = floor(A)
log,log2,log10	对数函数	y = log(A) y = log2(A) y = log10(A)
min/max	求最大值/最小值	y = min(x) y = min(x,z) y = min(x,[],dim) [y,loc]= min(x,[],dim)
norm	求1范数、2范数、∞范数	y = norm(x) y = norm(x,1) y = norm(x,2) y = norm(x,inf)
pnorm	求p范数	y = pnorm(x,q/r); y = pnorm(x,p,'power')

2.2 value函数

        value函数是最常用的决策变量处理函数之一，可以在优化问题求解成功之后，提取决策变量的取值，其语法如下：

Y = value(X)

例如，下面的代码就是在求解优化问题后求出决策变量与目标函数的取值：

sdpvar x y

objective = 2*x + 3*y;

Constraints = [x + y >= 2 , 2*x - 3*y <= 9 , x>=0];

optimize(Constraints,objective)

x = value(x)

y = value(y)

objective = value(objective)

运行结果如下：

   

        优化问题求解成功后，通过使用value函数我们可以知道该线性规划问题的目标函数2x+3y在(3,-1)处取得最小值3。

2.3 sdisplay函数

        sdisplay函数可以用来以符号的形式显示sdpvar变量，其语法如下：

s = sdisplay(p,[digits])

        其中，p为一个sdpvar变量，digits表示四舍五入的位数。例如：

x1 = sdpvar(1,1);

x2 = sdpvar(1,1);

f1 = x1^2 + 5*x2^2;

f2 = 3*x1^3 + x2;

m1 = sdisplay(f1)

m2 = sdisplay(f2)

m3 = sdisplay(f1*f2)

        运行结果为：

在调试代码的过程中，合理地应用sdisplay函数可以帮助我们确认目标函数或者约束条件的公式是否书写正确。

2.4 binmodel函数

        binmodel函数通过引入其他变量和约束，将涉及0-1变量和连续变量的多项式表达式转换为线性表达式，其语法如下：

[plin1,...,plinN,F] = binmodel(p1,...,pN,Domain)

其中plin1-plinN表示线性化之后的表达式，F表示相应的约束条件，p1-pN为初始表达式，Domain为连续变量的取值范围。下面是一个示例代码：

binvar a b

sdpvar x y

[plinear01,plinear02,F0] = binmodel(a^3+b,a*b);

[plinear1,plinear2,F] = binmodel(a^3*x+b*y,a*b*x, -2 <=[x,y] <=2);

        在上述代码中，plinear01对应线性化后的表达式a^3+b，plinear02对应于线性化之后的表达式a*b，F0为可行域，由于原始表达式中不包含连续变量，所以不需要指定取值范围；plinear1对应线性化后的表达式a^3*x+b*y，plinear2对应于线性化之后的表达式a*b*x，F0为可行域，连续变量的取值范围被限定在[-2,2]。

2.5 assign函数

        assign函数用来给sdpvar变量指定一个取值，其语法如下：

assign(X,value)

        例如下面的代码就是将变量x赋值为1

sdpvar x

assign(x,1)

value(x)

运行结果为：

 

2.6 is函数

        is函数用于检查sdpvar变量是否为某类型的变量，其语法如下：

d = is(x,property)

        当变量x满足属性’property’时，d取值为1，否则取值为0。下面的示例代码时检查变量是否为线性：

x = sdpvar(1,1);

y1 = x*x;

y2 = 2*x;

m1 = is(y1,'linear')

m2 = is(y2,'linear')

        运行结果为：

 

上面的代码中，变量y1为非线性，因此m1=0，y2为线性，因此m2=1。其他常用的类型如表3所示：

表3 is函数常用的判断类型

属性	含义
'real'	实数
'symmetric'	对称
'hermitian'	自共轭
'scalar'	标量
'linear'	线性
'bilinear'	双线性
'quadratic'	二次型
'integer'	整数
'binary'	0-1变量

2.7 int函数

        int函数使用sdpvar形式返回多项式的积分(注意只能返回多项式的积分，无法实现其他非线性表达式的积分)，其语法如下：

F = int(f,x,from,to)

        下面是一个例子：

sdpvar x1 x2 T

p = 4*x1^4 + x1*x2;

m1 = sdisplay(int(p))

m2 = sdisplay(int(p,x2))

m3 = sdisplay(int(p,[x1 x2],[0 0],[1 T]))

m4 = sdisplay(int(p,[x1 x2],[0 0],[1 x2]))

运行结果为：

上面的结果中，m1展示了对p中包含的所有变量求积分的结果；m2中只对变量x2求积分；m3中同时对变量x1和x2求积分，并指定了积分上下限。

2.8 jacobian函数

        jacobian函数以sdpvar变量形式返回多项式的导数，其语法如下：

J = jacobian(p)

J = jacobian(p,x)

其中，p为初始多项式，x为需要求导数的变量。下面是一个例子：

x1 = sdpvar(1,1);

x2 = sdpvar(1,1);

f = x1^2+5*x2^2;

m1 = sdisplay(jacobian(f))

m2 = sdisplay(jacobian(f,x2))

其运行结果为：

2.9 linearize函数

linearize函数用来求出多项式p(x)在x=value(x)处的切线表达式，其语法如下：

h = linearize(p)

例子：

x = sdpvar(1,1);

f = x^2;

assign(x,1);

m1 = sdisplay(linearize(f))



assign(x,3);

m2 = sdisplay(linearize(f))

运行结果：

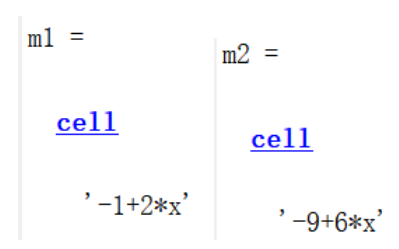
2.10 replace函数

        replace函数用于将一个sdpvar类型变量替换为另一个sdpvar类型变量、表达式或者常数，其语法如下：

newexpression = replace(expression,variable,replacement)

        例如，可以用常数替换表达式中对应的变量：

sdpvar x y a b

p = 1 + x^2 + y;

m1 = replace(p,[x y],[7 8])



p1 = replace(p,[x y],[a^2 b^4]);

m2 = sdisplay(p1)

运行结果为：

 

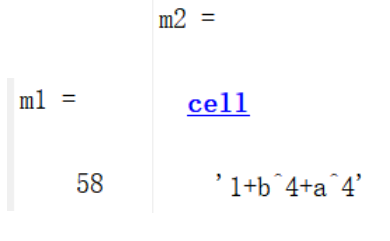
3.测试题

3.1测试1

求如下优化问题的解并将结果在命令行展示

3.2测试2

一汽车厂生产小、中、大三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求，利润以及每月工厂钢材、劳动时间的现有量如表4所示，试制定月生产计划，使工厂的利润最大。

表4 相关数据

	小型	中型	大型	现有量
钢材/吨	1.5	3	5	600
劳动时间/小时	280	250	400	60000
利润/万元	2	3	4

3.3测试3

请使用Yalmip工具箱求积分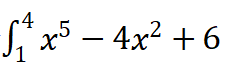的取值。

3.4测试4

请使用Yalmip工具箱求函数在点(-1,f(-1))处的切线方程。 

3.5测试题参考答案

第二章测试题的参考答案可以从下面的链接中获取：

https://download.csdn.net/download/weixin_44209907/88049325