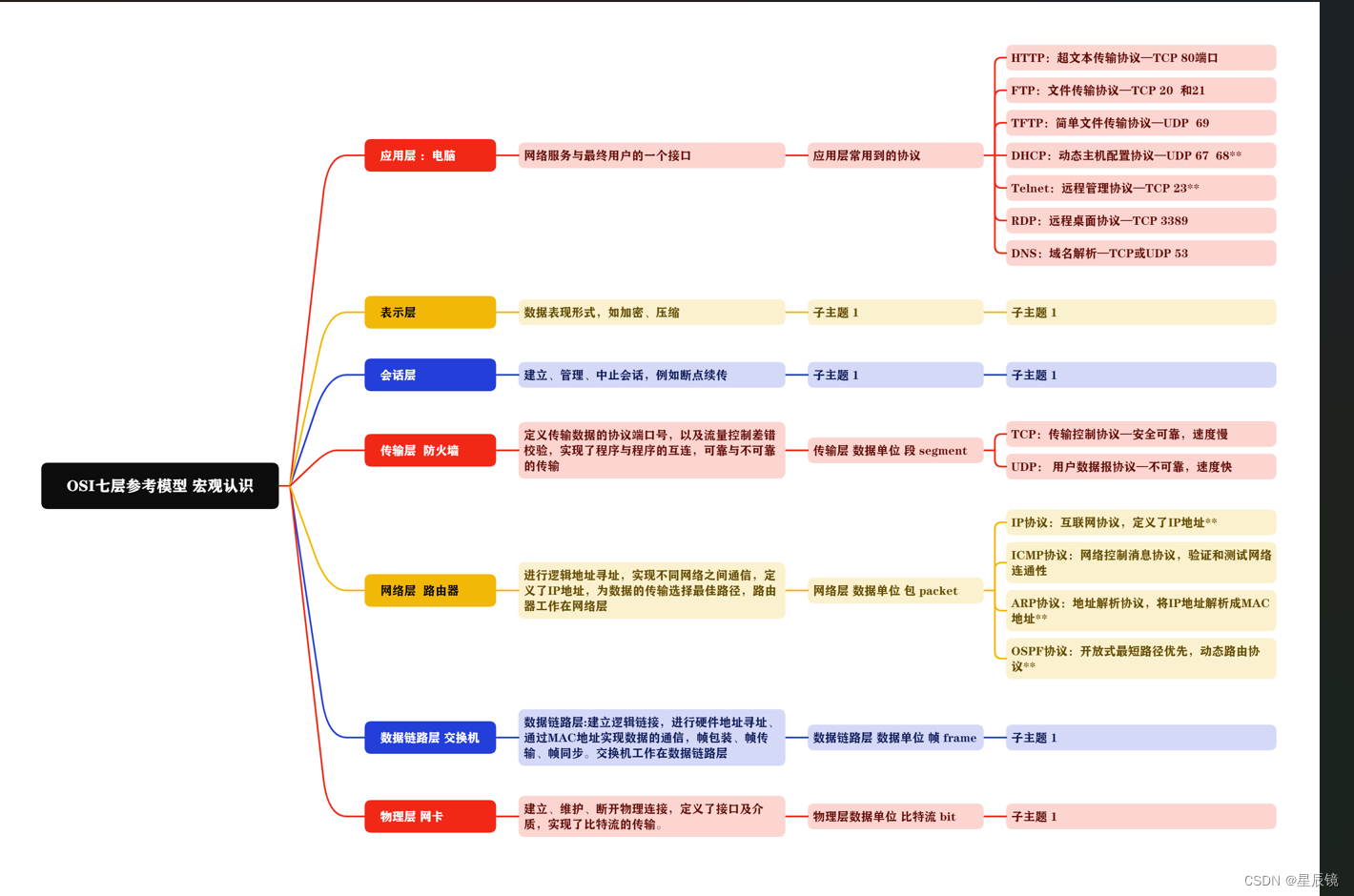
一、MPU6050简介
MPU6050是一款陀螺仪模块,可以测量X、Y、Z三轴的角速度和加速度,还带有温度传感器和数字运动处理器(DMP)。
二、学习步骤
1. I2C协议
MPU6050是通过I2C协议进行驱动的,配置寄存器和获取数据都需要通过I2C协议去实现开发板与MPU6050之间的通信。
2. MPU6050的相关寄存器
3. 数据处理
把获取到的原始数据进行处理,如通过互补滤波融合得到角度。
三、I2C协议
I2C协议通过数据总线SDA和时钟总线SCL去完成单片机与一些传感器模块的通信。SCL和SDA线根据I2C的协议的标准进行一系列高低电平的变化(时序)就可以完成信息的传输。
| 硬件I2C | 软件I2C |
| 通过硬件电路去实现的I2C协议 | 通过在单片机上找两个IO口去充当SCL和SDA线,再通过人为编写软件去控制SCL和SDA线的高低电平变化去模拟I2C协议 |
| 使用起来比较简单,执行速度比较快,耗时短;稳定性不一定好 | 通过软件模拟的,执行速度不如硬件I2C快,有一定的耗时,不过稳定性就比硬件I2C好 |
四. MPU6050硬件介绍

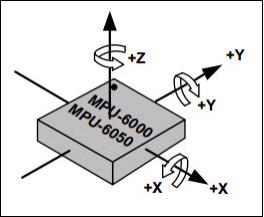
从MPU6050模块正面上我们还可以看到上面标注了X、Y轴的坐标系,那个就是MPU6050自身的坐标系,如下图所示。
以下是MPU6050的相关管脚,我们使用MPU6050时其实只需要用到VCC、GND、SCL和SDA这四个管脚。
| VCC | 3.3 - 5V(内部有稳压芯片) |
| GND | 地线 |
| SCL | MPU6050作为从机时IIC时钟线 |
| SDA | MPU6050作为从机时IIC数据线 |
| XCL | MPU6050作为主机时IIC时钟线 |
| XDA | MPU6050作为主机时IIC数据线 |
| AD0 | 地址管脚,该管脚决定了IIC地址的最低一位 |
| INT | 中断引脚 |
AD0管脚的作用:我们知道I2C通信中从机是要有的地址的,以区别多个从机。当AD0管脚接低电平时,从机地址是0xD0。从MPU6050的寄存器中我们可以得到答案,MPU6050作为一个I2C从机设备的时候,有8位地址,高7位的地址是固定的,就是WHO AM I 寄存器中的默认值—0x68,最低一位是由AD0的连线决定的。
读取MPU6050原始数据这个过程中一个很重要的思路就是一步一步,确保每步都正确后就很容易读出正确的数据。我们对MPU6050进行读写传感器数据就是对MPU6050的寄存器用I2C协议进行读写。对此我们还要了解MPU6050的寄存器,这个过程跟学习51单片机差不多,就是配置寄存器,读取相关数据。
五.MPU6050的几个重要寄存器
| SMPLRT_DIV寄存器 | 寄存器地址为0x19 |
| CONFIG寄存器 | 寄存器地址为0x1A |
| GYRO_CONFIG寄存器 | 寄存器地址为0x1B |
| 寄存器地址为0x1B | 寄存器地址为0x1C |
| 三轴加速度计的相关寄存器 | ACCEL_XOUT_H(0x3B) ACCEL_XOUT_L(0x3C) ACCEL_YOUT_H(0x3D) ACCEL_YOUT_L(0x3E) ACCEL_ZOUT_H(0x3F) ACCEL_ZOUT_H(0x40) |
| 三轴陀螺仪的相关寄存器 | GYRO_XOUT_H(0x43) GYRO_XOUT_L(0x44) GYRO_YOUT_H(0x45) GYRO_YOUT_L(0x46) GYRO_ZOUT_H(0x47) GYRO_ZOUT_H(0x48) |
| 温度传感器相关的寄存器 | TEMP_OUT_H(0x41) TEMP_OUT_L(0x42) |
| PWR_MGMT_1寄存器 | 寄存器地址为0x6B |
| WHO_AM_I寄存器 | 寄存器的地址为0x75 |
//初始化MPU6050
void InitMPU6050(){
Single_WriteI2C(PWR_MGMT_1, 0x00);//解除休眠状态
Single_WriteI2C(SMPLRT_DIV, 0x07);//陀螺仪采样率为1K/(1+0x07)=125Hz
Single_WriteI2C(CONFIG, 0x06); //低通滤波器的截止频率为1K,带宽为5Hz
Single_WriteI2C(GYRO_CONFIG, 0x18);//配置陀螺仪量程为2000deg/s,不自检
Single_WriteI2C(ACCEL_CONFIG, 0x00);//配置加速度计量程为2g,不自检
}六、原始数据的单位换算
由于MPU6050数据寄存器是一个16位的,由于最高位是符号位,故而数据寄存器的输出范围是-7FFF~7FFF ,也既是-32767~32767。
如果选择陀螺仪范围是±2000,那么意味着-32767对应的是-2000(°/s),32767对应是2000(°/s),当读取陀螺仪的值是1000时,对应的角速度计算如下:32767/2000 =1000/x; 既x = 1000/16.4(°/s),可以看出32767/2000 = 16.4 ,对应手册中的精度 16.4 LSB/(°/s),其他范围也是如此。
如果是加速度计,采用和陀螺仪同样的计算方法,当AFS_SEL=3时,数字-32767对应-16g,32767对应16g。把32767除以16,就可以得到2048, 即我们说的灵敏度。把从加速度计读出的数字除以2048,就可以换算成加速度的数值。举个例子,如果我们从加速度计读到的数字是1000,那么对应的加速度数据是1000/2048=0.49g。g为加速度的单位,重力加速度定义为1g, 等于9.8米每平方秒。
总结起来就是,只要对原始数据除以它在该量程下的灵敏度就可以获得实际的物理单位,原始数据时加速度的话,物理单位就为g,原始数据为角速度的话,物理单位就为°/s。
七、 角度换算(滤波算法)
1. 一阶互补滤波
void Get_Balance_Angle(void){
uint8 gyro_offset = 1;//静置时角速度的偏移量
float gyro_dt = 0.004f;//陀螺仪角速度积分系数,增长缓慢就增加
float Filter_weight = 0.02;//滤波权重
Get_GyroData();//获取原始三轴角速度
Get_AccData();//获取原始三轴加速度
g_fBalance_Gyro = mpu_gyro_y - gyro_offset;//原始角速度减去零偏值得到实际角速度
g_fAccel_Angle = (float)atan2(mpu_acc_x,mpu_acc_z) * 57.296;//两轴加速度求反三角得到加速度角度,乘以57.296,是把弧度转化为度
//一阶互补滤波核心公式,得到融合角度
g_fBalance_Angle = Filter_Weight * g_fAccel_Angle + (1-Filter_Weight) * (g_fBalance_Angle - g_fBalance_Gyro * gyro_dt);
}2. 清华角度滤波
/*
* 参数: G_angle——加速度计角度0-90内
* Gyro——陀螺仪角速度转花后的数值
* GRAVITY_ADJUST_TIME_CONSTANT——时间校正系数
DT——定时器时间 单位s
* 函数返回:无符号结果值
*/
void QingHua_AngleCalaulate(float G_angle,float Gyro){
float fDeltaValue;
g_fCarAngle = g_fGyroscopeAngleIntegral; //最终融合角度
fDeltaValue = (G_angle - g_fCarAngle) / GRAVITY_ADJUST_TIME_CONSTANT; //时间系数矫正
g_fGyroscopeAngleIntegral += (Gyro + fDeltaValue) * DT; //融合角度
}3、卡尔曼滤波(难理解)
float angle, angle_dot; //外部需要引用的变量
//angle_m为角速度角度和gyro_m为测到的角速度
void Kalman_Filter(float angle_m,float gyro_m){
const float Q_angle=0.001, Q_gyro=0.003, R_angle=0.5, dt=0.005;
//注意:dt的取值为kalman滤波器采样时间;
static float P[2][2] = { { 1, 0 },{ 0, 1 } };
static float Pdot[4] ={0,0,0,0};
static const char C_0 = 1;
static float q_bias, angle_err, PCt_0, PCt_1, E, K_0, K_1, t_0, t_1;
angle+=(gyro_m-q_bias) * dt;
Pdot[0]=Q_angle - P[0][1] - P[1][0];
Pdot[1]=- P[1][1];
Pdot[2]=- P[1][1];
Pdot[3]=Q_gyro;
P[0][0] += Pdot[0] * dt;
P[0][1] += Pdot[1] * dt;
P[1][0] += Pdot[2] * dt;
P[1][1] += Pdot[3] * dt;
angle_err = angle_m - angle;
PCt_0 = C_0 * P[0][0];
PCt_1 = C_0 * P[1][0];
E = R_angle + C_0 * PCt_0;
K_0 = PCt_0 / E;
K_1 = PCt_1 / E;
t_0 = PCt_0;
t_1 = C_0 * P[0][1];
P[0][0] -= K_0 * t_0;
P[0][1] -= K_0 * t_1;
P[1][0] -= K_1 * t_0;
P[1][1] -= K_1 * t_1;
angle += K_0 * angle_err;//最终融合角度
q_bias += K_1 * angle_err;
angle_dot = gyro_m-q_bias;//角速度
}