第四章 数学知识（三）——高斯消元，组合

news2025/11/4 22:12:39

文章目录

    • 高斯消元
    • 组合数
    • 高斯消元练习题
      • 884. 高斯消元解异或线性方程组
    • 组合数练习题
      • 885. 求组合数 I
      • 886. 求组合数 II
      • 887. 求组合数 III
      • 888. 求组合数 IV
      • 889. 满足条件的01序列

高斯消元

在 n 3 n^3 n3的时间复杂度内求解含有n个未知数的多元线性方程组
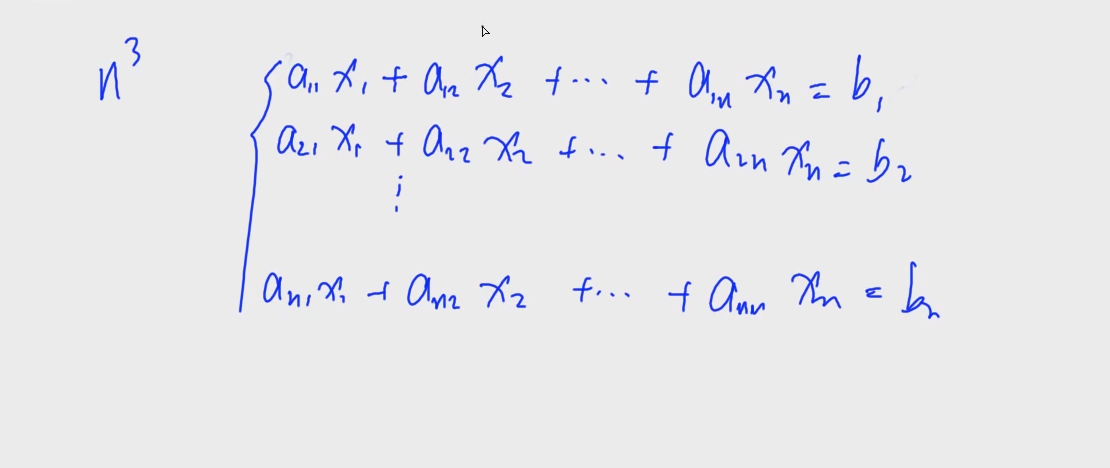
image.png
每一个方程表示为：
a i 1 x 1 + a i 2 x 2 + . . . + a i n x n = b i a_{i1}x_1 + a_{i2}x_2+...+a_{in}x_n=b_i ai1​x1​+ai2​x2​+...+ain​xn​=bi​
每个方程中有n个未知数，一共有n个这样的方程

方程的解有三种

  1. 无解
  2. 唯一解
  3. 无穷多解

用n * n + 1的系数矩阵表示以上方程组，其中第n + 1列表示 b i b_i bi​，对系数矩阵进行初等行变换以解方程，初等行变换有：

  1. 某一行乘以一个非零的数
  2. 交换某两行
  3. 把某行的若干倍加到另一行上
    初等行变换前后的方程组是等价的

将矩阵变换成上三角的形式，根据上三角的形式判断解的类型

  1. 唯一解：完美的阶梯型
  2. 无解：不是完美阶梯型，方程出现0 = !0的情况
  3. 无穷多解：不是完美阶梯型，方程出现0 = 0的情况
  • 找到当前列中绝对值最大元素所属的行
  • 将最大行与当前行交换
  • 用初等行变换将当前行的当前列元素变换成1
  • 用初等行变换，将当前元素往下的所有元素变换成0（这样的话当前列只有当前元素是非0的）

枚举所有列，每次都进行以上操作。需要注意的是：当最大元素为0时，跳过剩下步骤，直接枚举下一列。若跳过步骤，需要遍历下一列，依然遍历当前行。若完成了所有操作，需要遍历下一列与下一行

若行列式被化简成完美的阶梯型（每次的都是遍历下一列与下一行，即每次找到的最大元素非0），此时需要倒着求解：
矩阵中存储的是每个未知数的系数，每一行第一个未知数的系数都是1，使用初等行变换，只保留每一行的第一个非0系数，将该系数所属列的其他系数都变换成0

0表示无解，1表示唯一解，2表示无穷多解

模板：

int n;
double a[N][N];
const double eps = 1e-8;
// 用r遍历矩阵的行，c遍历矩阵的列，所以r和c表示当前行与当前列
int gauss()
{
	for (int c = 0, r = 0; c < n; ++ c )
	{
		int t = r;
		// 找出当前列的最大元素所属的行
		for (int i = r + 1; i < n; ++ i ) if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
		if (fabs(a[t][c]) < eps) continue;
		// 将最大元素所属的行与当前行交换（每个列元素的交换）
		for (int j = c; j <= n; ++ j ) swap(a[t][j], a[r][j]);
		// 用初等行变换将第一个非0元素变为1
		for (int j = n; j >= c; -- j ) a[r][j] /= a[r][c];
		// 用初等行变换，使得当前列往下的元素为0
		for (int i = r + 1; i < n; ++ i )
			if (fabs(a[i][c]) > eps)
				for (int j = n; j >= c; -- j )
					a[i][j] -= a[r][j] * a[i][c];
		
		r ++ ;
	}
	
	if (r < n) 
	{
		for (int i = r; i < n; ++ i )
		{
			if (fabs(a[i][n]) > eps) return 0; // 无解
		}
		return 2; // 无穷解
	}

	// 从最后一行开始更新b值
	for (int i = n - 1; i >= 0; -- i )
		for (int j = i + 1; j < n; ++ j )
			a[i][n] -= a[j][n] * a[i][j];
	return 1;
}

关于倒着求解：
若最后的矩阵是完美阶梯型，要获取未知数的解，就要使第i行只有第i个元素为1，其他元素都要为0，此时该方程为 x i x_i xi​ = b i b_i bi​
上面的模板中，第一个for之后，对于矩阵的第i行来说，只有前i - 1个元素为0，所以要把第i + 1到最后的元素用初等行变换变为0
由于第i行只有第i个元素为0，所以 a [ i ] [ j ] a[i][j] a[i][j]这个元素要想变成0，只能通过第 j j j行进行初等行变换
因为第j行的第j个元素为1，所以减去第j行的所有元素 * a [ i ] [ j ] a[i][j] a[i][j]，就能使 a [ i ] [ j ] a[i][j] a[i][j]为0
必要忘记将第i行的 b i b_i bi​值减去第j行的 b j b_j bj​ * a [ i ] [ j ] a[i][j] a[i][j]

组合数

C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab​=b!(a−b)!a!​
公式中，分母是b!，分子是a * a - 1 * a - 2 * ... * a - b + 1

一个重要的递推式：
C a b = C a − 1 b − 1 + C a − 1 b C_a^b=C_{a-1}^{b-1}+C_{a-1}^b Cab​=Ca−1b−1​+Ca−1b​
image.png
可以这么理解：从 a a a个物品中选择 b b b个物品，有几种选法？
从 a a a个物品中随便挑选一个物品，在剩下 a − 1 a-1 a−1个物品中选择 b b b个物品，此时有几种选法？
两种情况：
若选择之前挑好的物品，那么就要在剩下a-1个物品中选择b-1个物品，此时的选法为 C a − 1 b − 1 C_{a-1}^{b-1} Ca−1b−1​
若不选择之前挑好的物品，那么就要在剩下a-1个物品中选择b个物品，此时的选法为 C a − 1 b C_{a-1}^b Ca−1b​

将这两种情况相加，得到的就是从a个物品中选择b个物品的选法，即 C a b C_a^b Cab​

需要注意的是：
从n个物品中选择0个物品，此时的选法 C n 0 C_n^0 Cn0​ = 1
从0个物品中选择n个物品，此时的选法 C 0 n C_0^n C0n​ = 0

根据数据的范围以及精度问题，组合数求解分为4种

1 <= b <= a <= 2000

当题目中的a范围较小，要求该范围内的组合数时，可以直接使用上面的递推公式
C a b = C a − 1 b − 1 + C a − 1 b C_a^b=C_{a-1}^{b-1}+C_{a-1}^b Cab​=Ca−1b−1​+Ca−1b​
将范围内的所有组合数求出并保存，当询问某一组合数时，直接返回

模板：

const int N = 1e9 + 7;
int c[N][N];
for (int i = 0; i < N; ++ i) c[i][0] = 1;

for (int i = 1; i < N; ++ i)  
	for (int j = 1; j <= i; ++ j)
		c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;

1 <= b <= a <= 100000

根据组合数的定义：
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab​=b!(a−b)!a!​
对于范围内的数据，先预处理范围内数据的所有阶乘，之后这些阶乘将参与组合数的求解
需要注意的是：0的阶乘为1

当阶乘作为除数时，需要用快速幂求其逆元。为什么不能直接除以阶乘，反而要求其逆元呢？以下程序是两者的对比：
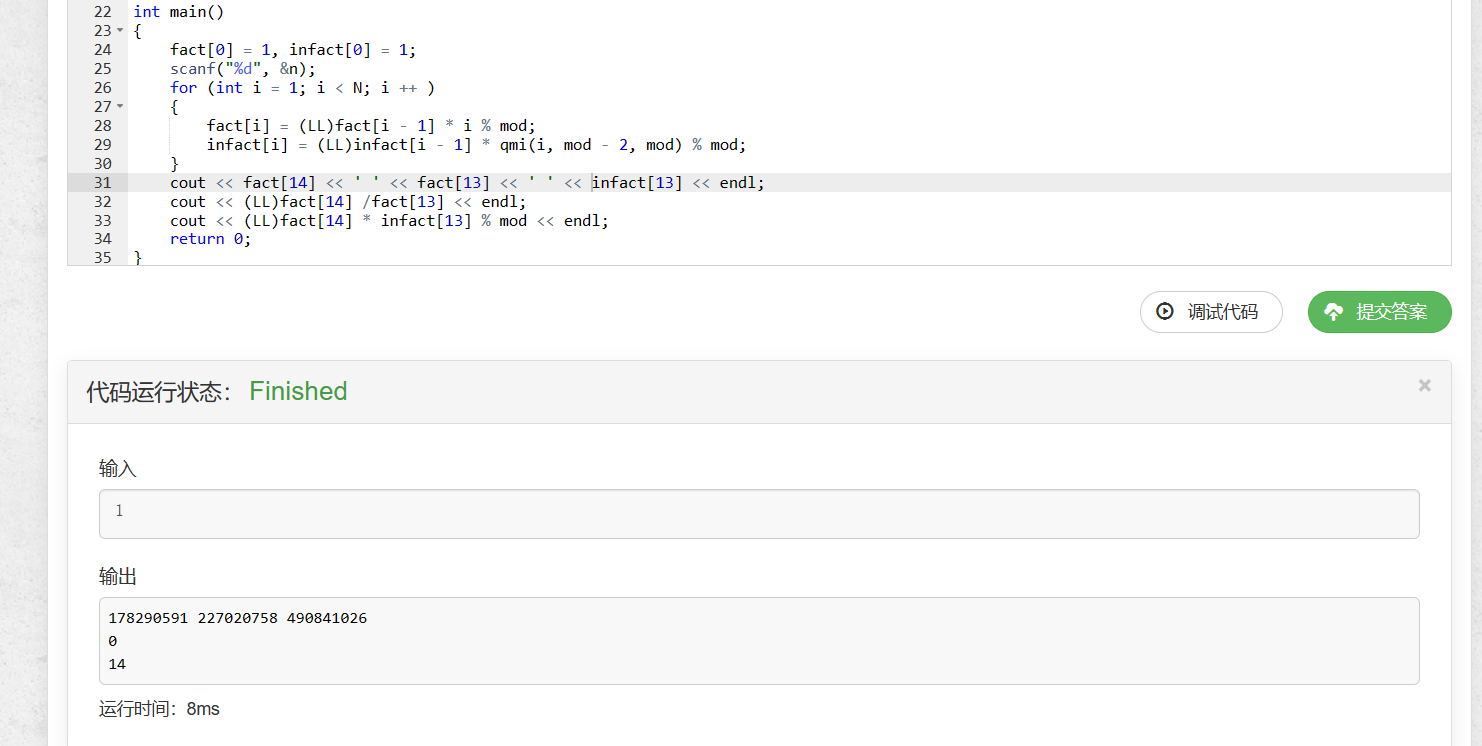
image.png

一个直接除以阶乘进行计算，一个乘以其逆元进行计算，只有乘逆元的运算结果是准确的。因为`(a / b) % m != (a % m) / (b % m)

所以我们要预处理两个数组，一个存储范围内数据的阶乘，一个存储阶乘的逆元
模板：

const int N, mod = 1e9 + 7;
int fact[N], infact[N];
fact[0] = 1, infact[0] = 1;
tyepdef long long LL;

int qmi(int a, int k, int p)
{
	int res = 1;
	while (k)
	{
		if (k & 1) res = (LL)res * a % p;
		a = (LL)a * a % p;
		k >>= 1;
	}
	return res;
}

for (int i = 1; i < N; ++ i ) 
{
	fact[i] = (LL)fact[i - 1] * i % mod;
	infact[i] = (LL)qmi(fact[i], mod - 2, mod) % mod;
}

int c = (LL)fact[a] * infact[b] % mod * infact[a - b] % mod;
pritnf("%d\n", c);

1 <= b <= a <= 1 0 18 10^{18} 1018

若p是质数，则有卢卡斯定理：
C a b ≡ C a   m o d   p b   m o d   p   C a / p b / p   ( m o d   p ) C_a^b ≡ C_{a\ mod\ p}^{b\ mod\ p}\ C_{a/p}^{b/p}\ (mod\ p) Cab​≡Ca mod pb mod p​ Ca/pb/p​ (mod p)
若数据范围很大，通过卢卡斯定理，我们就可以将数据缩小到p的范围内
若b / p, a / p还是大于p，那么继续使用卢卡斯定理，代码可以通过递归实现
当数据范围小于p时，直接通过定义求解组合数：
C a b = a ∗ ( a − 1 ) ∗ ( a − 2 ) ∗ . . . ∗ ( a − b + 1 ) b ! C_a^b=\frac{a*(a-1)*(a-2)*...*(a-b+1)}{b!} Cab​=b!a∗(a−1)∗(a−2)∗...∗(a−b+1)​
模板：

int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p)
{
    if (b > a) return 0;
    if (b > a - b) b = a - b;
    int x = 1, y = 1;
    for (int i = 0; i < b; ++ i )
    {
        x = (LL)x * (a - i) % p;
        y = (LL)y * (i + 1) % p;
    }
    return (LL)x * qmi(y, p - 2, p) % p;
}

int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

有性质：
C a b = C a a − b C_a^b=C_a^{a - b} Cab​=Caa−b​
所以当b > a - b时，可以将b = a - b，以减少组合数的计算次数
所以C函数中有if (b - a < b) b = b - a

高精度组合数

分解 C a b C_a^b Cab​的质因数，只实现高精度乘法即可

利用组合数的定义：
C a b = a ! b ! ( a − b ) ! C_a^b=\frac{a!}{b!(a-b)!} Cab​=b!(a−b)!a!​
计算 a ! a! a!， b ! b! b!和 ( a − b ) ! (a-b)! (a−b)!中所有质因子的出现次数，将 p i p_i pi​在 a ! a! a!中的出现次数减去 p i p_i pi​在 b ! b! b!和 ( a − b ) ! (a-b)! (a−b)!中的出现次数相加，就能得到 C a b C_a^b Cab​中 p i p_i pi​的出现次数k
那么
C a b = p 1 k 1   p 2 k 2   . . .   p n k n C_a^b=p_1^{k_1}\ p_2^{k_2}\ ...\ p_n^{k_n} Cab​=p1k1​​ p2k2​​ ... pnkn​​

对于 a ! a! a!，如何计算出它的某个质因子 p p p的个数？
a ! = [ a p ] + [ a p 2 ] + [ a p 3 ] + . . . a! = [\frac{a}{p}] + [\frac{a}{p^2}] + [\frac{a}{p^3}] + ... a!=[pa​]+[p2a​]+[p3a​]+...
a ! a! a!由 1 1 1, 2 2 2, 3 3 3, … , a a a这些数相乘，这些数也能分解质因数
若 a a a等于 p p p的 k k k倍（可能有余数），那么在 1 1 1, 2 2 2, 3 3 3, … , a a a这些数中，肯定存在 p p p的 k − 1 k - 1 k−1倍， p p p的 k − 2 k - 2 k−2倍，…， p p p的 1 1 1倍。因为这些数是连续的，这就表示 a ! a! a!中， p p p出现了 k k k次
而某个数等于 p p p的 n n n倍，说明该数的质因数分解中p出现了一次，但 p p p可能会出现2，3，…次，所以还需要判断 p 2 p^2 p2， p 3 p^3 p3，…是否在该数中出现
同样的，通过判断a是 p n p^n pn的几倍，知道 p n p^n pn在 a ! a! a!中出现的次数
再看上面的式子，当 p n > a p^n > a pn>a时，说明 a ! a! a!中不存在 p n p^n pn这个因数，此时计算停止

总结下步骤：

  1. 线性筛出 a a a的质数
  2. 求 C a b C_a^b Cab​中每个质数的出现次数
  3. 用高精度乘法将所有的质因数乘到一起得到 C a b C_a^b Cab​

模板：

int primes[N], cnt;
bool st[N];
int pcnt[N];

void get_primes(int n)
{
	for (int i = 2; i <= n; ++ i )
	{
		if (!st[i]) primes[cnt ++ ] = i;
		for (int j = 0; primes[j] <= i / j; ++ j )
		{
			st[primes[j] * i] = true;
			if (i % primes[j] == 0) break;
		}
	}
}

// 获取a!中质因数p的个数
int get(int a, int p)
{
	int res = 0;
	while (a)
	{
		res += a / p;
		a /= p;
	}
	return res;
}

vector<int> mul(vector<int>& a, int b)
{
	vector<int> c;
	int t = 0, s = a.size();
	for (int i = 0; i < s || t; ++ i )
	{
		if (i < s) t += a[i] * b;
		c.push_back(t % 10);
		t /= 10;
	}
	return c;
}

get_primes(a);
// 计算a!,b!和(a - b)!中，所有质数的出现次数并存储在pcnt中
for (int i = 0; i < cnt; ++ i )
{
	int p = primes[i];
	pcnt[i] = get(a, p) - get(b, p) - get(a - b, p); 
}

// 将所有质因数相乘得到最后的答案
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; ++ i )	
	for (int j = 0; j < pcnt[i]; ++ j )
		res = mul(res, primes[i]);

for (int i = res.size() - 1; i >= 0; -- i )
	printf("%d", res[i]);
printf("\n");

卡特兰数

直接看题：
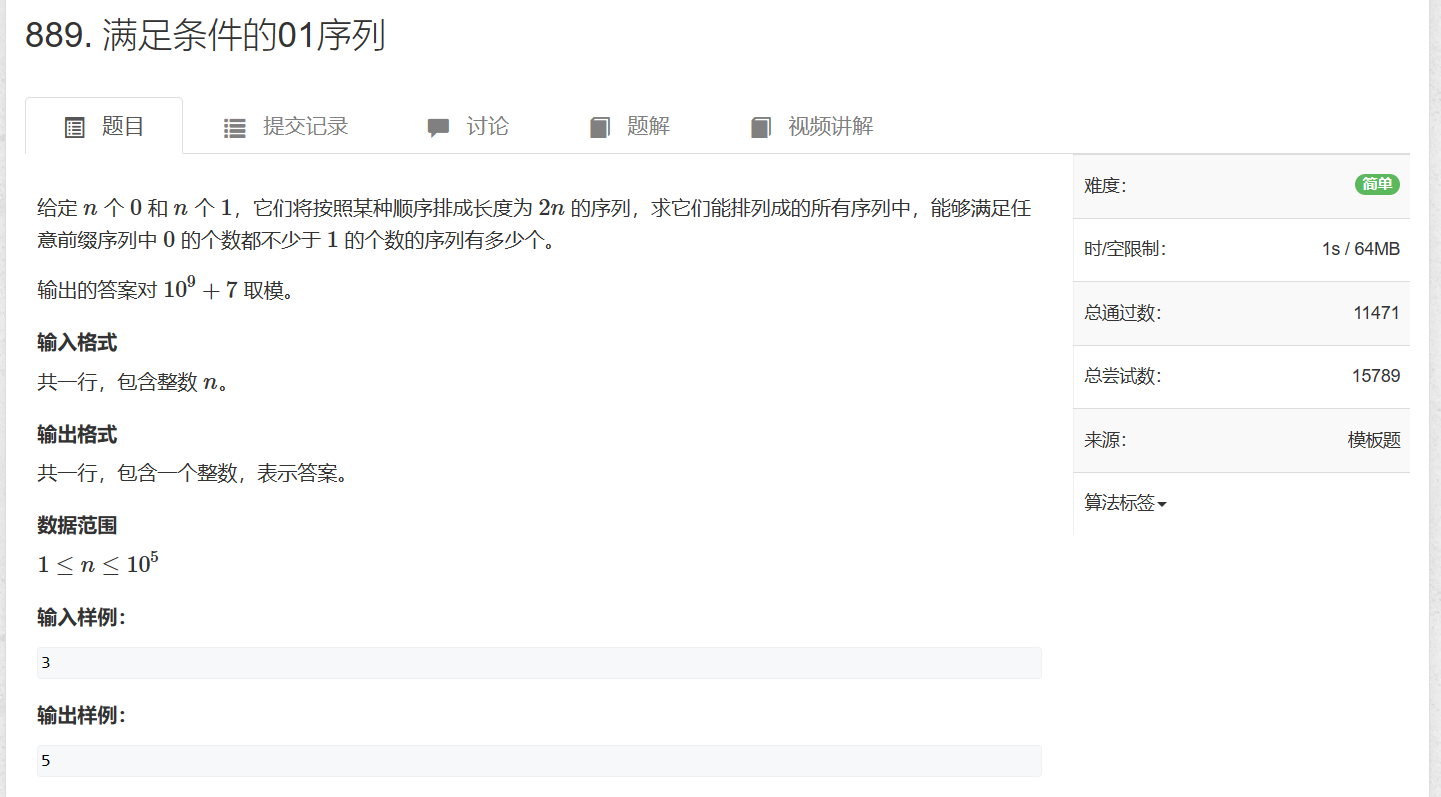
image.png
01序列可以转换成矩阵中的路径问题
0表示向右走一步，1表示向上走一步
题目给定n个0和n个1，我们就可以从(0, 0)开始走，最后走到(n, n)这个点
可以走几步？从2n步中选择n步向上或向右走，总共的步数就是 C 2 n n C_{2n}^n C2nn​

转换题目的限制条件：任意前缀中0的数量都要大于等于1的数量
也就是在坐标中x >= y，路径只能接触下图中的绿线并且位于绿线下方
当路径中的某个点接触到了红线，就说明该路径是一条不符合题目要求的路径
找出所有不符合题目要求的路径，将总的路径数减去不符合题意的路径数，就能得到我们想要的答案
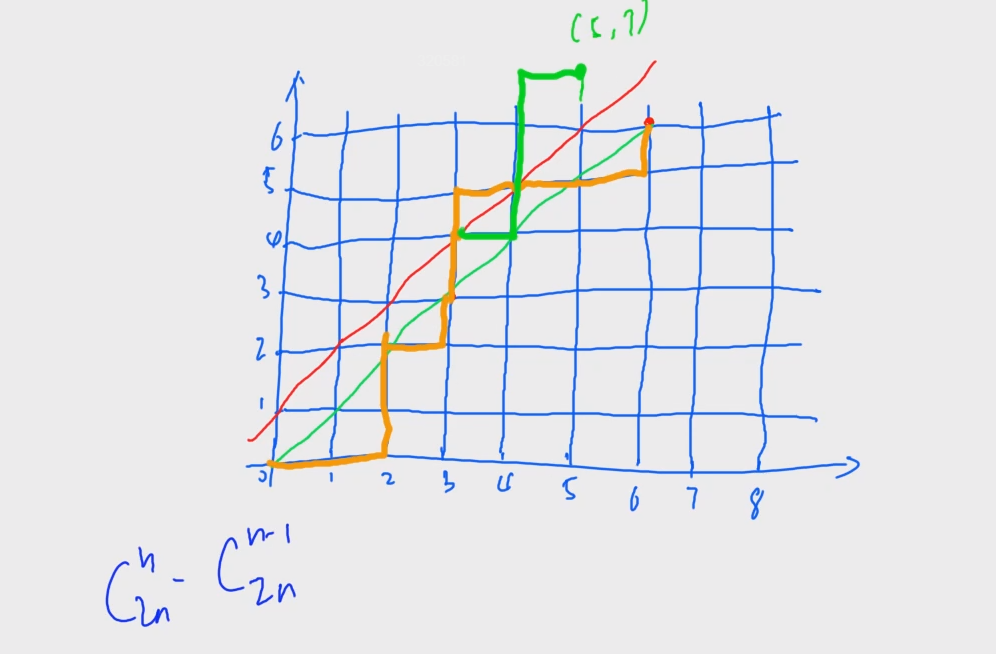
image.png
现在的问题是不符合题意的路径有几条？
假设一条路径接触或越过了红线，我们将这条路径中第一次与红线接触的点往后的路径，以红线为对称轴做轴对称
我们能发现所有不符合题意的路径最后都递达了(n - 1, n + 1)这个点
所以不符合题意的路径数为：从(0, 0)开始到(n - 1, n + 1)这个点的路径数，也就是 C 2 n n − 1 C_{2n}^{n-1} C2nn−1​

所以符合题意的路径数为：
C 2 n n − C 2 n n − 1 C_{2n}^n - C_{2n}^{n-1} C2nn​−C2nn−1​
将其化简得到：
C 2 n n n + 1 \frac{C_{2n}^n}{n+1} n+1C2nn​​

该数被称为卡特兰数

如何求解卡特兰数？根据数据范围从四种求组合数的方式种选择一种适合的即可

高斯消元练习题

883. 高斯消元解线性方程组 - AcWing题库
image.png

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;
const double eps = 1e-8;
const int N = 110;
double a[N][N];
int n;

int gauss()
{
    int c, r;
    for (c = 0, r = 0; c < n; ++ c)
    {
        int t = r;
        // 找当前列的最大元素所属的行
        for (int i = r + 1; i < n; ++ i )
            if (fabs(a[i][c]) > fabs(a[t][c])) t = i;
            
        if (fabs(a[t][c]) < eps) continue;
        // 将最大行与当前行交换
        for (int j = c; j <= n; ++ j ) swap(a[r][j], a[t][j]);
        // 初等行变换使当前行第一个元素为1
        for (int j = n; j >= c; -- j ) a[r][j] /= a[r][c];
        // 初等行变换使当前列以下的元素为0
        for (int i = r + 1; i < n; ++ i )
            if (fabs(a[i][c]) > eps)
                for (int j = n; j >= c; -- j )
                    a[i][j] -= a[i][c] * a[r][j];
        
        r ++ ;

    }
    if (r < n)
    {
        for (int i = r; i < n; ++ i )
            if (fabs(a[i][n]) > eps) return 0;
        return 2;
    }
    
    for (int i = n - 1; i >= 0; -- i )
        for (int j = i + 1; j < n; ++ j )
            a[i][n] -= a[i][j] * a[j][n];
            
    return 1;
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; ++ i )
        for (int j = 0; j <= n; ++ j )
            scanf("%lf", &a[i][j]);
    
    int t = gauss();
    if (t == 0) puts("No solution");
    else if (t == 2) puts("Infinite group solutions");
    else
    {
        for (int i = 0; i < n; ++ i )
            printf("%.2lf\n", a[i][n]);    
    }
    
    return 0;
}

debug：eps定义成int类型，应该定义成double类型，这是第二次犯了
倒着求解时，i应该等于r
fabs要记得加，老是忘

884. 高斯消元解异或线性方程组

884. 高斯消元解异或线性方程组 - AcWing题库
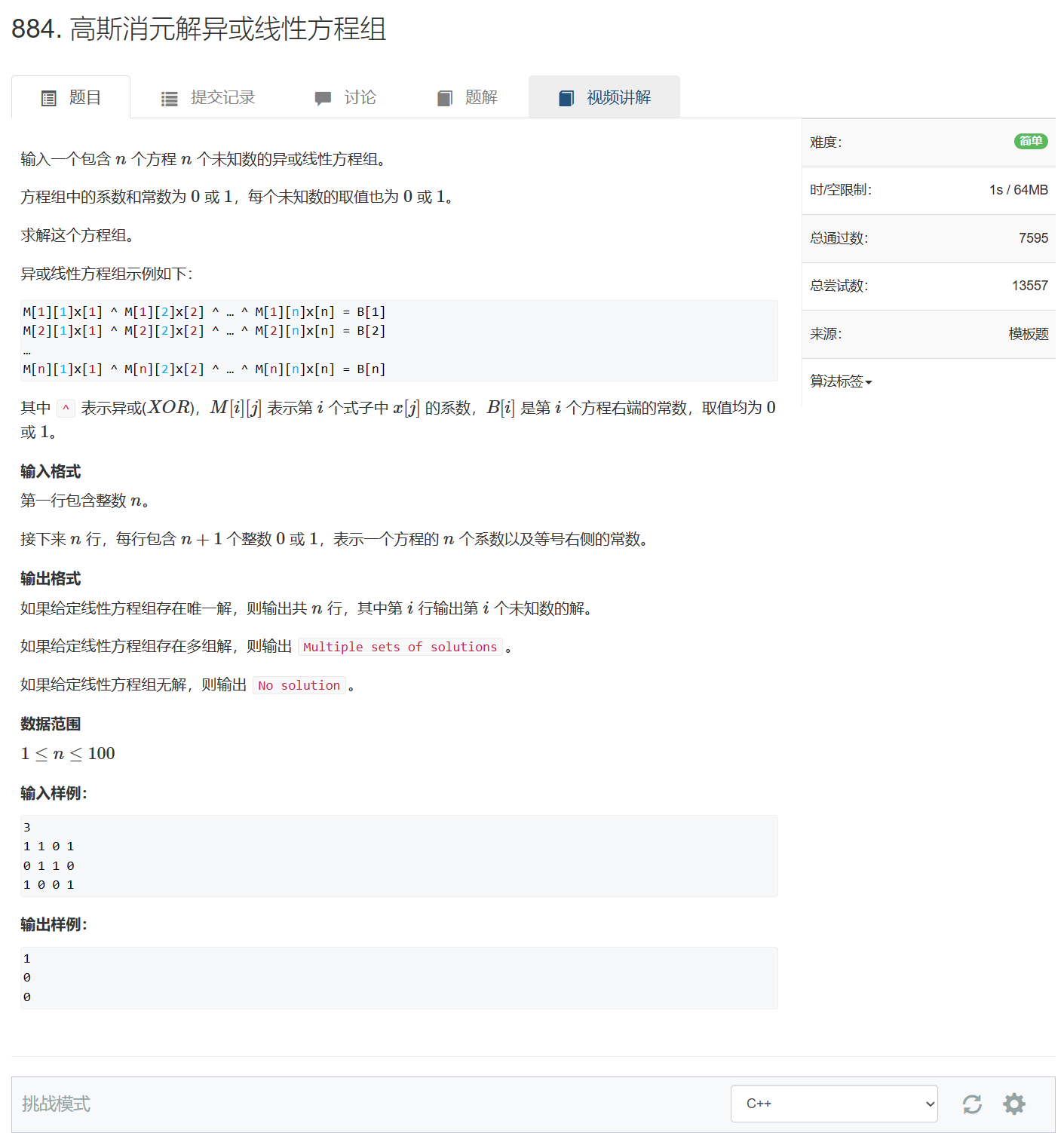
image.png

就是高斯消元的简单变形，初等行变换用异或体现就行了

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 110;
int a[N][N];
int n;

int gauss()
{
    int r = 1, c = 1;
    for (; c <= n; ++ c )
    {
        int t = -1;
        for (int i = r; i <= n; ++ i ) 
        {
            if (a[i][c]) 
            {
                t = i;
                break;
            }
        }
         
        if (t == -1) continue;
        
        for (int j = n + 1; j >= 1; -- j ) swap(a[t][j], a[r][j]);
        for (int i = r + 1; i <= n; ++ i )
            if (a[i][c])
                for (int j = c; j <= n + 1; ++ j )
                    a[i][j] ^= a[r][j];
                    
        r ++ ;
    }
    
    if (r != c)
    {
        for (int i = r; i <= n; ++ i )
            if (a[i][n + 1])
                return 0;
                
        return 2;
    }
    
    for (int i = n - 1; i >= 1; -- i )
        for (int j = i + 1; j <= n; ++ j )
            if (a[i][j]) a[i][n + 1] ^= a[j][n + 1];
            
    return 1;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; ++ i )
        for (int j = 1; j <= n + 1; ++ j )
            scanf("%d", &a[i][j]);
            
    int t = gauss();
    if (t == 2) puts("Multiple sets of solutions");
    else if (t == 0) puts("No solution");
    else for (int i = 1; i <= n; ++ i ) printf("%d\n", a[i][n + 1]);
    
    return 0;
}

debug：

for (int i = r; i <= n; ++ i ) 
{
	if (a[i][c]) 
	{
		t = i;
		break;
	}
}

t = i写成t = r
最后倒着求答案时
a[i][n + 1] ^= a[j][n + 1]写成a[i][n + 1] ^= a[j][n + i]，？这谁找得到啊

组合数练习题

885. 求组合数 I

885. 求组合数 I - AcWing题库
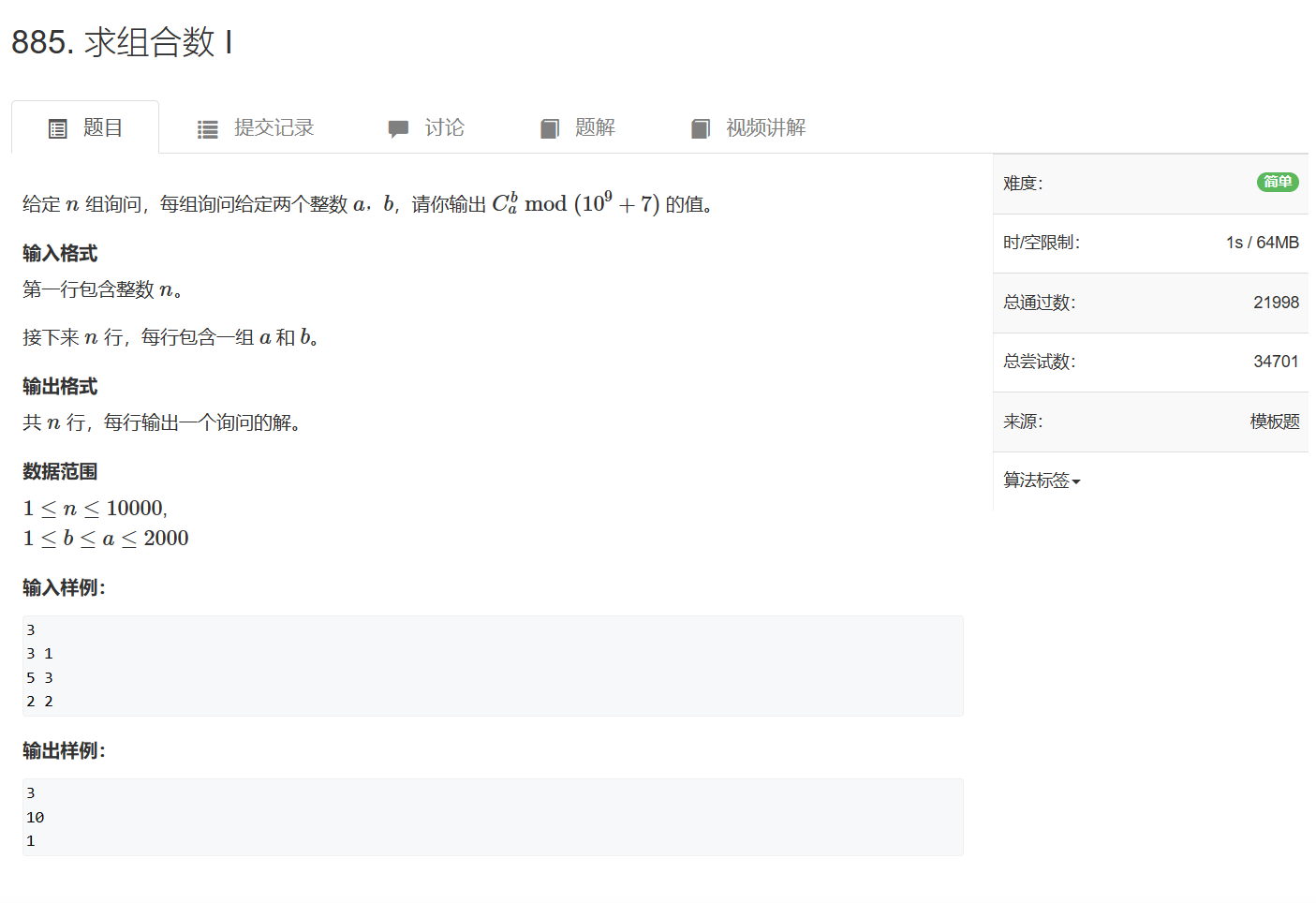
image.png

#include <iostream>
using namespace std;

const int N = 2010, mod = 1e9 + 7;
int c[N][N];
int n;

void init()
{
    for (int i = 0; i < N; ++ i) c[i][0] = 1;
    
    for (int i = 1; i < N; ++ i)  
        for (int j = 1; j <= i; ++ j)
            c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}

int main()
{
    init();
    
    scanf("%d", &n);
    int a, b;
    while (n -- )
    {
        scanf("%d%d", &a, &b);
        printf("%d\n", c[a][b]);
    }
    
    return 0;
}

886. 求组合数 II

886. 求组合数 II - AcWing题库
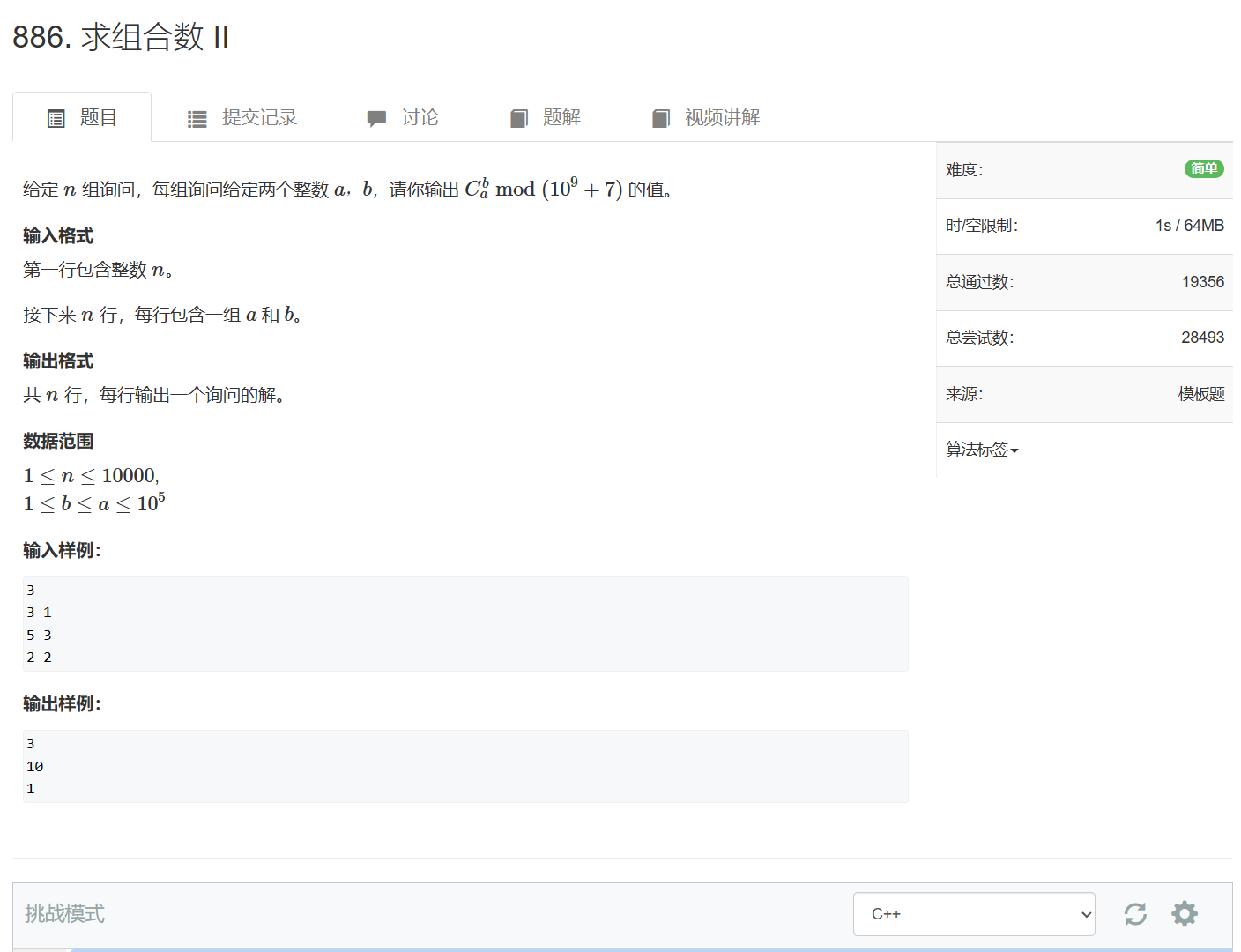
image.png

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 100010, mod = 1e9 + 7;
int n, fact[N], infact[N];

int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % mod;
        k >>= 1;
    }
    return res;
}

int main()
{
    fact[0] = 1, infact[0] = 1;
    for (int i = 1; i < N; ++ i )
    {
        fact[i] = (LL)fact[i - 1] * i % mod;
        infact[i] = (LL)qmi(fact[i], mod - 2, mod) % mod;
    }
    scanf("%d", &n);
    int a, b;
    while (n -- )
    {
        scanf("%d%d", &a, &b);
        int c = (LL)fact[a] * infact[b] % mod * infact[a - b] % mod;
        printf("%d\n", c);
    }
    
    return 0;
}

887. 求组合数 III

887. 求组合数 III - AcWing题库
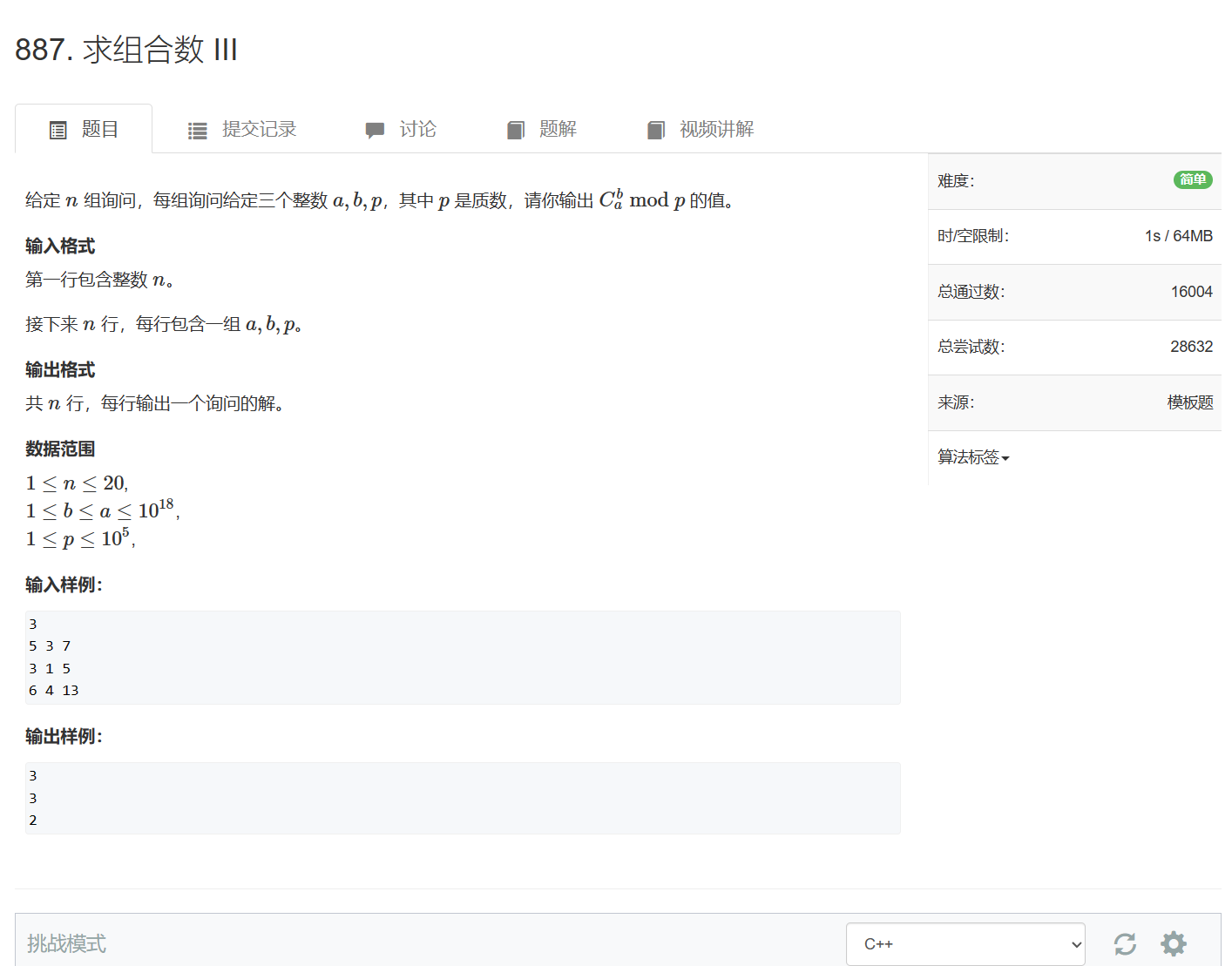
image.png

#include <iostream>
using namespace std;
typedef long long LL;
int n;

int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

int C(int a, int b, int p)
{
    if (b > a) return 0;
    if (b > a - b) b = a - b;
    int x = 1, y = 1;
    for (int i = 0; i < b; ++ i )
    {
        x = (LL)x * (a - i) % p;
        y = (LL)y * (i + 1) % p;
    }
    return (LL)x * qmi(y, p - 2, p) % p;
}

int lucas(LL a, LL b, int p)
{
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

int main()
{
    scanf("%d", &n);
    LL a, b;
    int p;
    while (n -- )
    {
        scanf("%lld%lld%d", &a, &b, &p);
        printf("%d\n", lucas(a, b, p));
    }
    return 0;
}

debug：有一个乘法运算没有LL的强转，导致爆int，最后出现负数
所以每次的乘法都要检查是否有LL的强转以及模p

888. 求组合数 IV

888. 求组合数 IV - AcWing题库
image.png

#include <iostream>
#include <vector>
using namespace std;

const int N = 5010;
int cnt, primes[N], pcnt[N];
bool st[N];

void get_primes( int n )
{
    for (int i = 2; i <= n; ++ i )
    {
        if (!st[i]) primes[cnt ++ ] = i;
        for (int j = 0; primes[j] <= n / i; ++ j )
        {
            st[ primes[j] * i ] = true;
            if ( i % primes[j] == 0 ) break;
        }
    }
}

int get(int a, int p)
{
    int res = 0;
    while (a)
    {
        res += a / p;
        a /= p;
    }
    return res;
}

vector<int> mul(vector<int>& a, int b)
{
    vector<int> c;
    int t = 0, s = a.size();
    
    for ( int i = 0; i < s || t; ++ i )
    {
        if (i < s) t += a[i] * b;
        c.push_back( t % 10 );
        t /= 10;
    }
    return c;
}

int main()
{
    int a, b;
    scanf("%d%d", &a, &b);
    
    get_primes(a);
    for (int i = 0; i < cnt; ++ i )
    {
        int p = primes[i];
        pcnt[i] = get(a, p) - get(b, p) - get(a - b, p);
    }
    
    vector<int> res;
    res.push_back(1);
    
 
    for (int i = 0; i < cnt; ++ i )
        for (int j = 0; j < pcnt[i]; ++ j )
            res = mul(res, primes[i]);
            
    for (int i = res.size() - 1; i >= 0; -- i ) printf("%d", res[i]);
    printf("\n");
    return 0;
}

889. 满足条件的01序列

889. 满足条件的01序列 - AcWing题库
image.png

由于这道题的数据范围在10000以内，所以直接根据定义求组合数即可

#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10, mod = 1e9 + 7;

int n;

int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % mod;
        a = (LL)a * a % mod;
        k >>= 1;
    }
    return res;
}

int main()
{
    scanf("%d", &n);
    int a = 2 * n, b = n;
    
    int res = 1, y = 1;
    for (int i = 0; i < b; ++ i )
    {
        res = (LL)res * (a - i) % mod;
        y = (LL)y * (i + 1) % mod;
    }
    
    res = (LL)res * qmi(y, mod - 2, mod) % mod;
    res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
    printf("%d\n", res);
    
    return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/752420.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【AUTOSAR】：NvM

【AUTOSAR】：NvM

Autosar的NvM理解 AUTOSAR_SWS_NVRAMManager.pdf块的定义块的管理类型块的状态重点梳理：几个常用的API函数AUTOSAR_SWS_MemoryAbstractionInterface.pdf里面对存储的HAL抽象衍生出几个重要的MainFunctionNV (non volatile)：非亦失性，也就是我们需要将数据存储到Flash或外部E…
阅读更多...
谈谈企业未来如何实现有序用电

谈谈企业未来如何实现有序用电

摘 要&#xff1a;风光发电的大比例发展将对电网需要的转动惯量和备用产生致命影响&#xff0c;严重威胁电网的平稳运行&#xff0c;本文结合AcrelEMS企业微电网系统谈谈企业如何应对。 关键词&#xff1a;有序用电 调节负荷 综合能源管理 企业微电网 0 引言 自2020年9月以来&…
阅读更多...
android linker加载和链接机制

android linker加载和链接机制

文章目录 So的加载和启动So文件的读取与加载工作ReadProgramHeaderReserveAddressSpaceLoadSegmentsFindPhdr so 的链接机制动态节区 执行so文件原文地址&#xff1a; So的加载和启动 handledlopen(pathName,PTLD_LAZY)&#xff1b;//获得指定文件的句柄&#xff0c;这个handl…
阅读更多...
SpringAMQP - 消息传输时，如何提高性能？解决 SQL 注入问题？

SpringAMQP - 消息传输时，如何提高性能？解决 SQL 注入问题？

目录 一、问题背景 二、从消息转化器根源解决问题 1.引入依赖 2.在服务生产者和消费者中都重新定义一个 MessageConverter&#xff0c;注入到 Spring 容器中 一、问题背景 在SpringAMQP的发送方法中&#xff0c;接收消息的类型是Object&#xff0c;也就是说我们可以发送任意…
阅读更多...
【程序人生】如何在工作中保持稳定的情绪？

【程序人生】如何在工作中保持稳定的情绪？

前言 在工作中保持稳定的情绪是现代生活中一个备受关注的话题。随着职场压力和工作挑战的增加&#xff0c;我们常常发现自己情绪波动不定&#xff0c;甚至受到负面情绪的困扰。然而&#xff0c;保持稳定的情绪对于我们的工作效率、人际关系和整体幸福感都至关重要。 无论你是…
阅读更多...
GPT-4揭秘：从科学突破到宇宙探索，大模型如何为人类谋福祉？

GPT-4揭秘：从科学突破到宇宙探索，大模型如何为人类谋福祉？

最近一段时间&#xff0c;人工智能领域似乎在上演一场密切相关的三幕戏。从OpenAI的GPT-4&#xff0c;到LeanDojo的开源平台&#xff0c;再到Elon Musk的xAI&#xff0c;人工智能的最新发展进程仿佛正在向我们揭示未来的模样。让我们深入探讨一下这些最新的科技发展。 GPT-4&a…
阅读更多...
个人信息保护影响评估，推动个人信息保护“关口前移”

个人信息保护影响评估，推动个人信息保护“关口前移”

2021 年 11 月 1 日&#xff0c;《个人信息保护法》&#xff08;以下简称《个保法》&#xff09;的正式施行&#xff0c;可以说在我国个人信息保护法治建设具有里程碑意义。《个保法》内容具备系统性、针对性和可操作性特点&#xff0c;规范了个人信息处理活动&#xff0c;明确…
阅读更多...
ubuntu安装软件包提示【未安装软件包 deepin-elf-verify】【已解决】

ubuntu安装软件包提示【未安装软件包 deepin-elf-verify】【已解决】

文章目录 背景原因分析步骤1 解压文件2 删除依赖3 重新打包软件 转载请标明出处&#xff1a; https://bigmaning.blog.csdn.net/article/details/131713280 本文出自:【BigManing的博客】 背景 在ubuntu系统上安装一个deb文件&#xff0c;执行命令后&#xff0c;报错如下 sud…
阅读更多...
【C++】STL之string功能及模拟实现

【C++】STL之string功能及模拟实现

目录 前沿 一、标准库中的string类 二、string类的常用接口说明 1、string类对象的常见构造 2、string类对象的容量操作 3、string类对象的访问及遍历操作 4、string类对象的修改操作 5、string类非成员函数 6、vs下string结构的说明 三、string类的模拟实现 1、构造函数 2…
阅读更多...
MySQL(备份还原索引视图入门)

MySQL(备份还原索引视图入门)

文章目录 第一节 备份和还原1、题目2、题目作答 第二节 索引1.题目2.题目作答 第三节 视图1 题目2 题目作答 第一节 备份和还原 1、题目 CREATE DATABASE beifen;use beifen;CREATE TABLE books(bk_id INT NOT NULL PRIMARY KEY,bk_title VARCHAR(50) NOT NULL,copyright YEA…
阅读更多...
django框架向DRF框架演变过程详解

django框架向DRF框架演变过程详解

一、Django框架实现项目查询接口 主要知识点&#xff1a; Django框架视图函数 1、在 Django 项目中创建一个应用&#xff08;如果还没有创建&#xff09;&#xff1a; python manage.py startapp projects 2、在项目的 models.py 文件中定义项目模型 from django.db impor…
阅读更多...
视频融合平台EasyCVR登录后通道数据及菜单栏页面显示异常的排查与解决

视频融合平台EasyCVR登录后通道数据及菜单栏页面显示异常的排查与解决

EasyCVR可拓展性强、视频能力灵活、部署轻快&#xff0c;可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等&#xff0c;以及厂家私有协议与SDK接入&#xff0c;包括海康Ehome、海大宇等设备的SDK等&#xff0c;能对外分发RTSP、RTMP、FLV、HLS、WebRTC等格式的视频流。 有用…
阅读更多...
只需三步实现Gateway结合Sentinel实现无侵入网关限流，注意避坑!

只需三步实现Gateway结合Sentinel实现无侵入网关限流，注意避坑!

前言&#xff1a;本文基于您已有基础的可运行的微服务系统&#xff0c;使用了Sping Cloud Alibaba&#xff0c;Gateway,Nacos等&#xff1b;目标实现网关流控类型的限流。 顾名思义限流用于在高并发场景下限制请求流量的进入&#xff0c;保护系统不被冲垮。阿里巴巴的开源senti…
阅读更多...
数据库慢查询优化

数据库慢查询优化

数据库慢查询优化 1.分析慢查询原因 分析导致慢查询的原因是数据库性能优化的关键步骤之一。下面是一些常见的方法和工具&#xff0c;可以帮助你确定慢查询的原因&#xff1a; 慢查询日志&#xff1a; 开启慢查询日志&#xff0c;允许数据库记录执行时间超过阈值的查询语句。…
阅读更多...
百度ERNIE 3.0——中文情感分析实战

百度ERNIE 3.0——中文情感分析实战

目录 前言一、百度ERNIE 3.0二、使用ERNIE 3.0中文预训练模型进行句子级别的情感分析2-1、环境2-2、数据集加载2-3、加载预训练模型和分词器2-4、基于预训练模型的数据处理2-5、数据训练和评估2-6、模型验证2-7、情感分析结果的预测以及保存 三、自定义个人案例3-1、如何自定义…
阅读更多...
数据库语句

数据库语句

文章目录 数据库语句SQL语言分类MySQL中6种常见的约束1.DDL1.1 创建新的数据库1.2 创建新的表1.3 删除指定的数据表 2.DML管理表2.1 插入数据2.2 修改&#xff08;更新数据&#xff09;2.3 在数据表中删除指定的数据 3.DQL查询数据记录4.DCL4.1 修改表名和表结构4.2 扩展表结构…
阅读更多...
Node.js详解（四）：连接MongoDB

Node.js详解（四）：连接MongoDB

文章目录 一、安装MongoDB访问驱动二、连接数据库三、添加数据四、添加多条数据五、修改数据六、查询数据1、查询单条记录2、查询多条记录 七、删除数据八、完整示例代码1、路由 Api 接口&#xff1a;2、运行结果&#xff1a; MongoDB 对许多平台都提供驱动可以访问数据库&…
阅读更多...
前端vue入门(纯代码)31_route-link的repalce属性

前端vue入门(纯代码)31_route-link的repalce属性

如果夜里十二点我还回你消息&#xff0c;那么意味着什么&#xff0c;意味着我是真的很喜欢玩手机。 【29.Vue Router--router-link的replace属性】 <router-link>的replace属性 replace属性的作用是&#xff1a;控制路由跳转时操作浏览器历史记录的模式。【当我们从一个…
阅读更多...
城市内涝监测设备-内涝监测终端

城市内涝监测设备-内涝监测终端

随着我国城市化发展迅速、全球极端天气现象频发带来的暴雨天气增多&#xff0c;汛期暴雨引发道路低洼处、立交桥底、隧道、涵洞等城市 内涝时有发生&#xff0c;甚至开启城市看海模式&#xff0c;对交通、电力、通讯等造成了严重的影响和破坏&#xff0c;严重时造成人民生命、财…
阅读更多...
放弃使用Merge，开心拥抱Rebase！

放弃使用Merge，开心拥抱Rebase！

1. 引言 大家好&#xff0c;我是比特桃。Git 作为现在最流行的版本管理工具&#xff0c;想必大家在开发过程中都会使用。由于 Git 中很多操作默认是采用 Merge 进行的&#xff0c;并且相对也不容易出错&#xff0c;所以很多人都会使用 Merge 来进行合并代码。但Rebase 作为 Gi…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023