文章目录
- 一、排序的概念
- 排序的概念
- 排序的稳定性
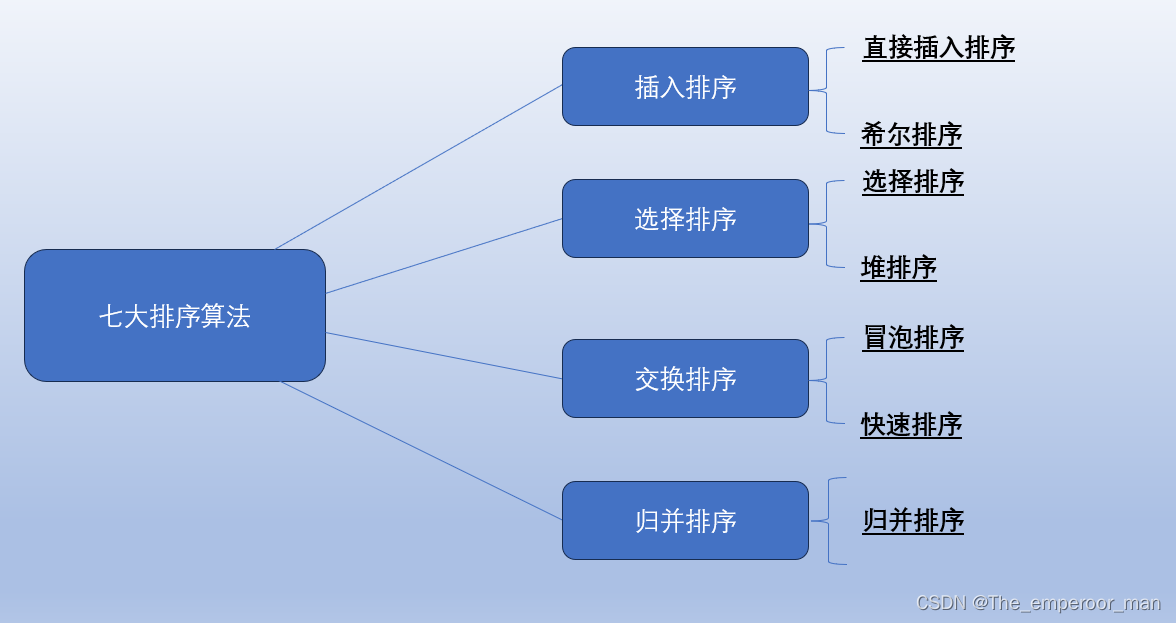
- 七大排序算法
- 二、堆排序
- 核心思想
- 代码实现
- 三、性能分析
- 四、七大排序算法
一、排序的概念
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
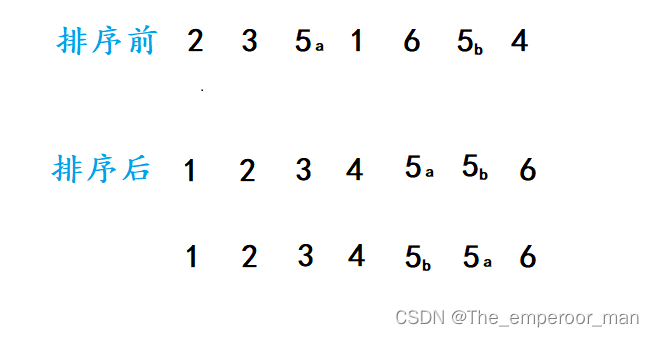
排序的稳定性
上述待排序的数中,有两个5。 将前面的5标记一个a, 将后面的5标记一个b。
通过算法进行排序后,这一组数就有序了, 但是要看两个相同的5的位置是否有改变。
5a仍在5b前面,那么这个排序算法就是稳定的 ,
5a跑到了5b后面,那么这个排序算法就是不稳定的 。
一个稳定的排序算法可以做到不稳定,
不稳定的排序算法一定做不到稳定。
至于为什么要讨论这个稳定性, 是为了以后应用到实际场景上。 比如,一场数学考试, 假设a用了30分钟做完了,并得了满分。
假设b用了一个小时做完了,并得了满分。 此时a与b都是得了满分,但是用的时间不一样,所以两个人的排名又会有所不同。
七大排序算法
二、堆排序
核心思想
基本思想:堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆。
如何创建大根堆 / 小根堆
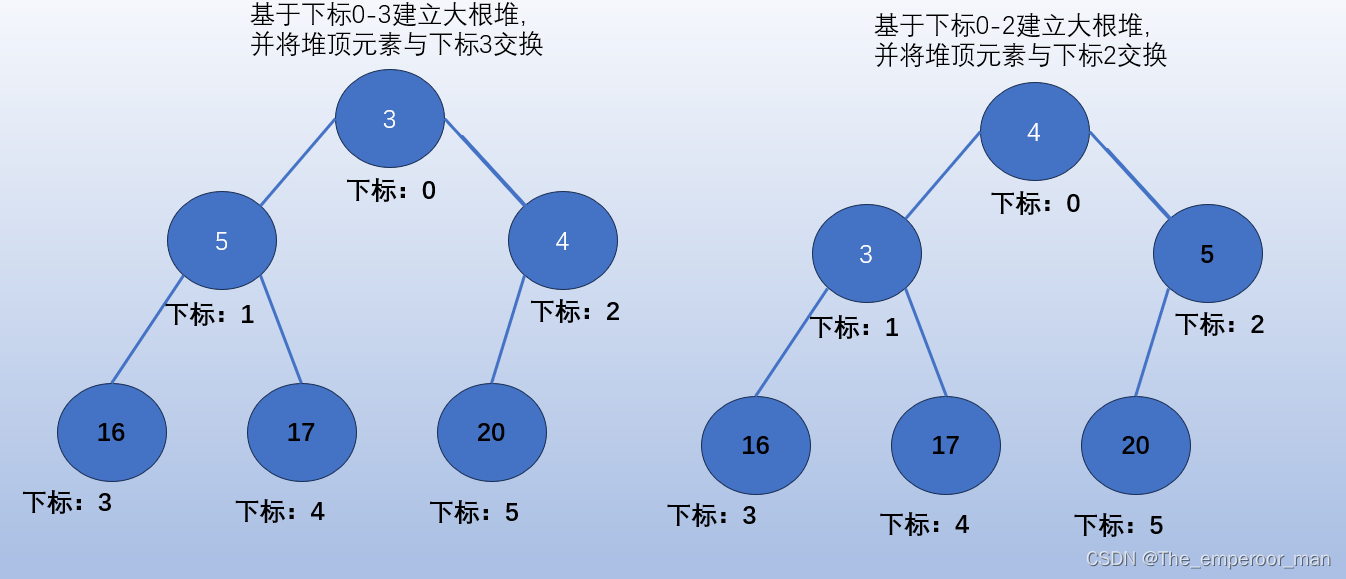
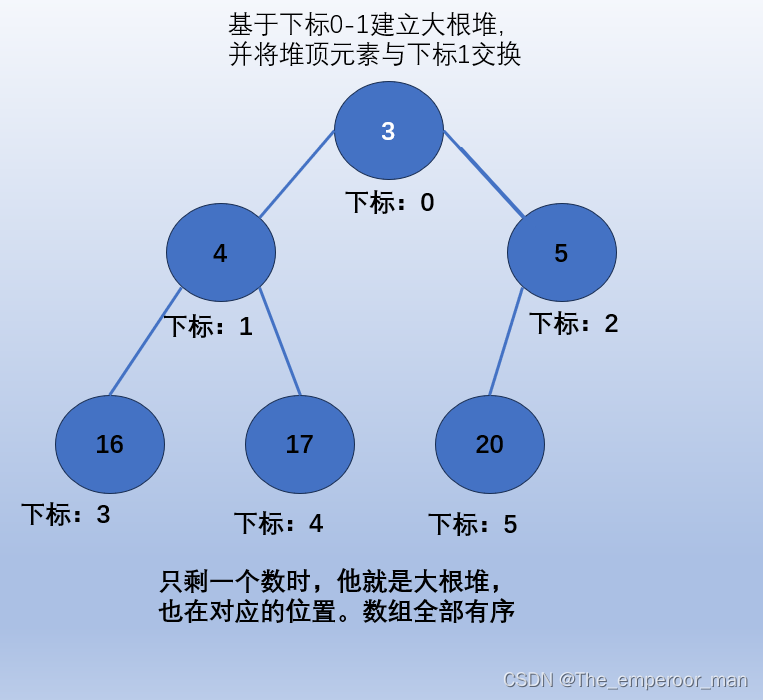
图解
有一组待排序数列,我们进行升序排序。
黑色数字为已经在对应位置的数,无序再参加创建大根堆,也无序交换。
>
说白了就是:利用堆的性质,找到这些数中最大或最小的数,然后放到应有的位置,再让剩下的数去建立堆,再调整位置。
重复这个过程,就可以有序。
代码实现
代码实现
public class HeapSort {
/**
* 堆排序
* 时间复杂度:O(n*logn)
* 空间复杂度:O(1)
* 稳定性:不稳定
* @param array
*/
public static void heapSort(int[] array) {
createBigHeap(array);
int end = array.length-1;
while (end>0) {
int tmp = array[end];
array[end] = array[0];
array[0] = tmp;
shiftDown(array,0,end);
end--;
}
}
// 将整个数组建立成大根堆
private static void createBigHeap(int[] array) {
for (int parent = (array.length-2)/2; parent > 0; parent--) {
shiftDown(array,parent, array.length);
}
}
// 向下调整下标parent —— len的数
private static void shiftDown(int[] array,int parent,int len) {
int child = parent*2+1;
while (child < len) {
if(child + 1<len && array[child] < array[child+1]) {
child++;
}
if(array[parent] < array[child]) {
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
parent = child;
child = parent*2+1;
}else break;
}
}
}
三、性能分析
堆排序的特性总结:
堆排序使用堆来选数,效率就高了很多。
时间复杂度:O(N*logN)
空间复杂度:O(1)
稳定性:不稳定
四、七大排序算法

想学哪个点哪个
归并排序讲解
快速排序讲解
直接插入排序讲解
希尔排序讲解
直接选择排序讲解
堆排序讲解
冒泡排序讲解