数值的整数次方

描述

实现函数 double Power(double base, int exponent)，求base的exponent次方。

注意：

1.保证base和exponent不同时为0。

2.不得使用库函数，同时不需要考虑大数问题

3.有特殊判题，不用考虑小数点后面0的位数。

数据范围：$∣base∣≤100 $，$ ∣exponent∣≤100 $，保证最终结果一定满足$ ∣val∣≤10^4 $

进阶：空间复杂度 $O (1)$ ，时间复杂度$ O(n)$

示例1

输入：

2.00000,3

返回值：

8.00000

示例2

输入：

2.10000,3

返回值：

9.26100

示例3

输入：

2.00000,-2

返回值：

0.25000

说明：

2的-2次方等于1/4=0.25

思路

一个很简单的方法就是用for循环不断累乘即可，但需要注意判断当exponent为负时需要对base取倒数，并且exponent需要取相反数，即

if (exponent < 0) {
    exponent = -exponent;
    base = 1 / base;
}

然后用for循环累乘即可

double result = 1;
for (int i = 0; i < exponent; i++) {
    result *= base;
}
return result;

需要注意的是当exponent为0时，任何数的0次方都为1，但由于result初始化为1了，所以不需要再进行特殊情况讨论

下面可以使用递归分治法来解决这个问题

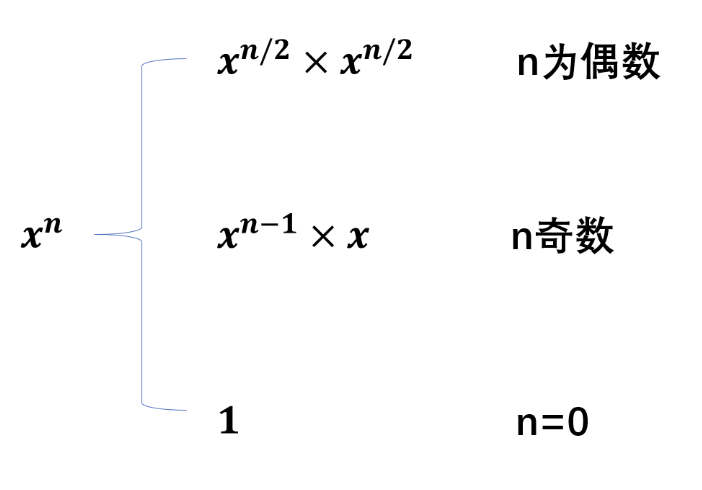
分治的思路就是将一个大问题分为许多相同的子问题，最后再将子问题合并为原问题的解。对于这个题目，假如题目求2⁴，一般情况下先求2，2²，2³。如果使用分治法，将2⁴分为两个2²相乘，然后再将2²分为两个2相乘，可以提高计算的效率，具体步骤就是

对于0次方，直接返回结果1
对于exponent为负数的情况，先将exponent取反，再对base取倒数
如果exponent为偶数，则通过递归计算exponent的一半的结果，然后将其平方
如果exponent为奇数，则先递归计算exponent - 1的结果，然后乘以base

即如下图

alt

if (exponent == 0) {
    return 1; // 任何数的0次方都等于1
} else if (exponent < 0) {
    return 1 / Power(base, -exponent); // 处理负指数
} else if (exponent % 2 == 0) {
    double temp = Power(base, exponent / 2); // 使用递归计算指数的一半
    return temp * temp;
} else {
    return base * Power(base, exponent - 1); // 使用递归计算指数-1的结果
}

完整代码

import java.util.*;
public class Solution {
    public double Power(double base, int exponent) {
       if (exponent == 0) {
            return 1; // 任何数的0次方都等于1
        } else if (exponent < 0) {
            return 1 / Power(base, -exponent); // 处理负指数
        } else if (exponent % 2 == 0) {
            double temp = Power(base, exponent / 2); // 使用递归计算指数的一半
            return temp * temp;
        } else {
            return base * Power(base, exponent - 1); // 使用递归计算指数-1的结果
        }
    }
}