文章目录
- 题目
- 基本设计思想
- 代码实现
- 效果
题目
定义三元组(a,b,c)(a,b,c均为整数)的距离D=|a-b|+|b-c|+|c-a|。给定3个非空集合S1,S2,S3,按升序分别存储在三个数组中。请设计一个尽可能高效的算法,计算并输出所有有可能的三元组中的最小距离。例如S1 = {-1,0,9},S2 = {-25,-10,10,11},S3 = {2,9,17,30,41},则最小距离为2,相应的三元组为(9,10,9)。要求:
- 给出算法的基本设计思想。
- 根据设计思想,用C/C++实现算法。
- 说明所设计的算法的时间复杂度和空间复杂度。
基本设计思想
- 根据题目要求,需要给出三个升序数组中元素组成三元组的最小距离D。首先可以想到的是最朴素的算法,三层循环遍历三个数,计算最小距离D,得出最小值。该算法的时间复杂度达到O(n^3),空间复杂度也达到O(n)。
- 因此,我们可以考虑类似双指针的算法,我们使用三个指针 i、j、k 分别指向三个数组的起始位置,并根据当前三个元素的距离来更新最小距离和结果。我们通过比较当前三个元素中的最小值来决定哪个指针移动,以使得距离更接近。最终得到最小距离D即为题目所求。
代码实现
int LinearList::Question_14()
{
Array arr1,arr2,arr3;
arr1.length = 5;
cout<<"insert 5 nums to arr1:"<<endl;
for(int i = 0;i < arr1.length;i ++)
{
cin >> arr1.data[i];
}
arr2.length = 5;
cout<<"insert 5 nums to arr2:"<<endl;
for(int i = 0;i < arr2.length;i ++)
{
cin >> arr2.data[i];
}
arr3.length = 5;
cout<<"insert 5 nums to arr3:"<<endl;
for(int i = 0;i < arr3.length;i ++)
{
cin >> arr3.data[i];
}
int n1 = arr1.length;
int n2 = arr2.length;
int n3 = arr3.length;
int i = 0, j = 0, k = 0; // 三个指针分别指向三个数组的起始位置
int minDistance = INT_MAX;
std::vector<int> result;
while (i < n1 && j < n2 && k < n3) { //三指针计算最小距离D
int a = arr1.data[i], b = arr2.data[j], c = arr3.data[k];
int distance = std::abs(a - b) + std::abs(b - c) + std::abs(c - a);
if (distance < minDistance) {
minDistance = distance;
result = { a, b, c };
}
// 移动指针以使得距离更接近
if (a <= b && a <= c) {
i++;
} else if (b <= a && b <= c) {
j++;
} else {
k++;
}
}
cout << "Min Distance Triple: ";
for (int t = 0; t < result.size(); t++) {
cout << result[t] << " ";
}
cout << endl;
return minDistance;
}
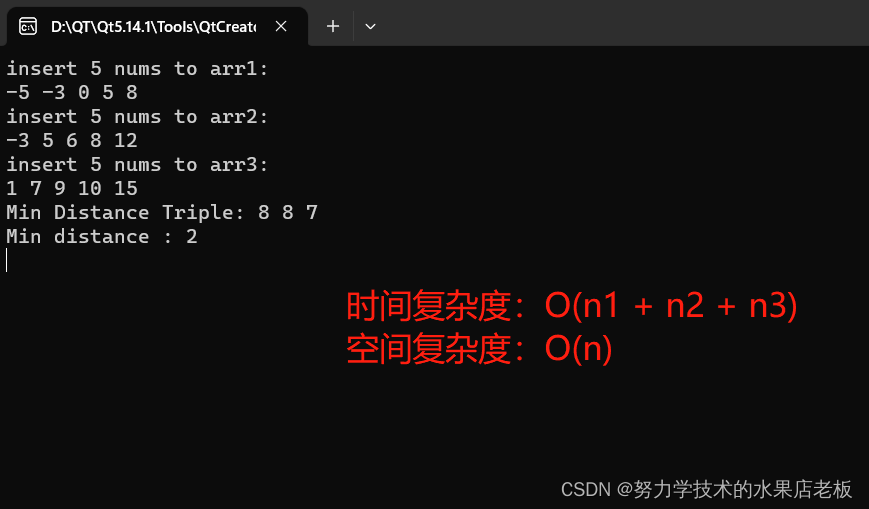
效果