问题描述
在一个长度为 n 的数组中选择 10 个元素,使得 10个元素的和 与 该元组中元素总和的 1/10 接近
问题约束
数组长度 n:10 <= n <= 100;
数组中没有重复的数字,所以选择的10个元素中也没有重复的数字
遗传算法原理
请移步我上一篇的博客 基于遗传算法解决流水车间调度问题
构建该问题遗传算法模型
染色体编码
每个染色体编码成随机选择的10个元素序列,比如 [1,2,3,4,5,6,7,0,8,9]
基因交换、变异
在遗传算法中,可以将问题的一个可行解看成一条染色体,染色体在配对时发生基因交换或者发生基因变异生成新的染色体,即新的可行解。
而新产生的可行解(染色体)参与到下一次基因配对中,产生另一些新的可行解。
基因交换
'''
如果交换前的解为
【1 2 3 4 5】 解1
【4 2 5 1 3】 解2
要交换部分为
【2 3 4】
【2 5 1】
交换后解为
【1 2 5 1 5】 解3
【4 2 3 4 3】 解4
我们发现此时两个解中的元素有重复,需要进一步约束
下面就是进一步约束
此时 解1 的 头(head) 为 【1】,被交换过来的部分为 【2 5 1】,交换给解2的部分为 【2 3 4】,其中 1 重复,所以将重复的 解1 的 头(head) 更改为 被交换过来的部分1和交换过去的部分同一位置的数,所以 解3 的头(head) 为 4
解1 的 尾(tail)也一样,改为 3
所以最后的 解3 为 【4 2 5 1 3】
解4 为 【1 2 3 4 5】
'''
基因突变
# 基因突变,从 长度为 n 的数组中随机挑选一个选择替换可行解中的任意一个元素,需要保证替换的元素不能和已有元素重复
# 如:原来的解为 【1,2,3,4,5】,基因突变后 【1,2,17,4,5】
适应度
由于问题目标是:10个元素的和 与 该元组中元素总和的 1/10 接近。
所以在该问题中可行解中10个元素的和 与 该数组中元素总和的 1/10 越接近适应度就越高,即差值的绝对值越小,适应度越高,有适应度公式
适
应
度
=
1
/
a
b
s
(
10
个
元
素
和
−
所
有
元
素
和
/
10
)
适应度 = 1/ abs(10个元素和-所有元素和/10)
适应度=1/abs(10个元素和−所有元素和/10)
注意:
有可能随机到的可行解和总和的 1/10 正好相等,但 1/0 会报错,考虑到 是 1/10,所以如果差值不为 0,那么最小的差值是 0.1,即适应度为 10,很显然相等的情况适应度最高,所以将其适应值设置为 11
适应度映射为概率之后的归一化处理
适应度映射为概率
适 应 度 / 适 应 度 的 总 和 = 计 算 映 射 后 的 概 率 适应度 / 适应度的总和=计算映射后的概率 适应度/适应度的总和=计算映射后的概率
归一化处理
伪代码如下:
此时概率列表为 [0.2, 0.3, 0.7, 1.0]
概率 = random.random()
for i in 列表:
if 概率 < i:
选择 i 对应的染色体
break 退出循环
'''
解释
如果此时随机的概率为 0.1,那么 0.1<0.2,选择 0.2 所对应的染色体
如果此时随机的概率为 0.5,那么 0.5>0.2, 0.5>0.3, 0.5<0.7, 选择 0.7 所对应的染色体——在判断 0.5和0.7的关系之前,循环已经判断了 0.5 和 0.2,0.3 之间的大小关系,所以在判断0.5 和0.7的关系时,我们已经保证了此时 随机的概率(0.5)不在0.2和0.3的概率范围之内
'''
具体代码如下
P_guiyi_list = [P_list[0]] + [P_list[i] for i in range(1, len(P_list))] # 归一之后的概率列表
for i in range(N):
P_num = random.random()
for j in range(len(P_guiyi_list)):
if P_num-j < 0:
finally_data.append(init_data[j])
break
染色体配对(复制)
遗传算法配对选择的方式多种多样,对该问题我们选择轮盘赌法进行染色体选择。
- 轮盘赌法——将个体适应度大小映射为概率进行复制:适应度高的个体有更大概率复制,且复制的分数越多。
- 将适应度大小映射为概率——比如此时有20个可行解,那么就有20个适应度(比如说 1/路程 ),那么每个可行解映射后的概率为 该可行解的适应度 / 20个可行解的总和
- 轮盘赌法的详细介绍(个人理解)—— 比如一开始问题的可行解有20个,即20个染色体,在第一次俩俩配对后生成 N 个可行解,此时问题的可行解有 20+N 个(其中可能有重复的可行解),然后对这 20+N 个可行解的适应度进行降序排序,选择 20+N 个可行解中适应度前 20 的可行解进行下一次染色体配对
遗传算法代码
随机生成长度为 n 的数组
import random
num_list_len = random.randint(10,100)
num_list = []
for i in range(num_list_len):
num = random.randint(1, 500)
while num in num_list:
num = random.randint(1, 500)
num_list.append(num)
# 长度为 n:num_list_len
# 随机生成的数组:num_list
参数介绍
N = 50 # 种群规模
T = 200 # 迭代次数
PM = 0.05 # 变异概率
PC = 0.7 # 交换概率
num_list_len # 数组长度
num_list # 数组列表
初始化染色体(可行解)
def init(N):
"""
初始化染色体
:param N:
:return:
"""
init_data = []
for j in range(N):
init_list = []
for i in range(10):
rand_num = random.randint(0, num_list_len-1)
while num_list[rand_num] in init_list:
rand_num = random.randint(0, num_list_len-1)
init_list.append(num_list[rand_num])
init_data.append(init_list)
return init_data
计算适应度
def fitness(init_data):
"""
计算适应度
:param init_data: --> list
:param N: --> num
:return:
"""
fit_list = []
for i in range(len(init_data)):
sum_num = abs(sum(init_data[i])-sum(num_list)/10)
if sum_num == 0:
fit = 11
else:
fit = 1 / sum_num # fit 越高,适应度越高
fit_list.append((fit, i))
# print(fit_list)
return fit_list
# fit 是该可行解的适应度,i 是该可行解的索引
# i 的意义是 当对 fit 进行排序时,通过 i 对排序之后适应度相对应的可行解进行排序
基因交换
def change(solve_list):
"""
PC = 0.7
:param solve_list: --> 染色体种群
:return: solve_list: --> 经过基因交换后的染色体种群
"""
# 选择父代列表和母代列表
male_list = solve_list[0::2]
female_list = solve_list[1::2]
# print(male, female)
for j in range(len(solve_list)):
# 选择需要交换基因的两个个体
# print(j)
if random.random() < 0.7:
male = male_list[random.randint(0, len(male_list)-1)]
female = female_list[random.randint(0, len(female_list)-1)]
# 两个个体之间的基因交换
random_index1 = random.randint(0, len(male)-1) # 要交换部分的起始索引点
random_index2 = random.randint(0, len(male)-1) # 要交换部分的末尾索引点
while random_index2 <= random_index1:
random_index1 = random.randint(0, len(male) - 1)
random_index2 = random.randint(0, len(male) - 1)
# child1, child2 = male[0:random_index1] + female[random_index1:random_index2] + male[random_index2:], female[0:random_index1] + male[random_index1:random_index2] + female[random_index2:]
child1_head = []
child1_tail = []
for i in male[0:random_index1]:
num = i
while num in female[random_index1:random_index2]:
num = male[random_index1:random_index2][female[random_index1:random_index2].index(num)]
child1_head.append(num)
for i in male[random_index2:]:
num = i
while num in female[random_index1:random_index2]:
num = male[random_index1:random_index2][female[random_index1:random_index2].index(num)]
child1_tail.append(num)
child1 = child1_head + female[random_index1:random_index2] + child1_tail
child2_head = []
child2_tail = []
# 子代2头
for i in female[0:random_index1]:
num = i
while num in male[random_index1:random_index2]:
num = female[random_index1:random_index2][male[random_index1:random_index2].index(num)]
child2_head.append(num)
# 子代2尾
for i in female[random_index2:]:
num = i
while num in male[random_index1:random_index2]:
num = female[random_index1:random_index2][male[random_index1:random_index2].index(num)]
child2_tail.append(num)
child2 = child2_head + male[random_index1:random_index2] + child2_tail
# print(len(set(child1)), len(set(child2)))
solve_list.append(child1)
solve_list.append(child2)
return solve_list
基因变异
def mata(solve_list):
"""
基因突变
PM = 0.05 变异概率
:param solve_list: --> 染色体种群
:return: solve_list: --> 经过基因交换后的染色体种群
"""
for i in solve_list:
if random.random() < PM:
# print(i)
change_index = random.randint(0, len(i)-1)
rand_num = random.randint(0, num_list_len-1)
while num_list[rand_num] in i:
rand_num = random.randint(0, num_list_len - 1)
i[change_index] = num_list[rand_num]
solve_list.append(i)
# print(i)
return solve_list
归一化处理以及染色体选择复制
def guiyi(init_data, fit_list):
"""
归一化处理以及染色体选择复制
:param init_data:
:param fit_list:
:return: init_data
"""
finally_data = []
# 适应度(可行解)排序
# print(init_data)
fit_list.sort()
fit_list = fit_list[::-1]
# print(fit_list)
index_list = [i[1] for i in fit_list]
init_data = [init_data[i] for i in index_list][0:N]
fit_list = fit_list[0:N]
# print(init_data)
# 概率归一化处理
num_list = [i[0] for i in fit_list]
P_list = [i / sum(num_list) for i in num_list] # 概率列表
P_guiyi_list = [P_list[0]] + [P_list[i] for i in range(1, len(P_list))] # 归一之后的概率列表
# 轮盘赌法染色体选择复制
for i in range(N):
P_num = random.random()
for j in range(len(P_guiyi_list)):
if P_num-j < 0:
finally_data.append(init_data[j])
break
return finally_data
迭代
init_data = init(N) # 初始化可行解
for i in range(T+1):
fit_list = fitness(init_data) # 计算适应度
init_data = guiyi(init_data, fit_list) # 轮盘赌法选择 N 规模的 可行解
# 输出迭代结果
fit_list = fitness(init_data)
fit_list.sort()
res_index_list = (max(fit_list)[1], min(fit_list)[1])
res_list = [sum(init_data[res_index_list[0]]), sum(init_data[res_index_list[1]])]
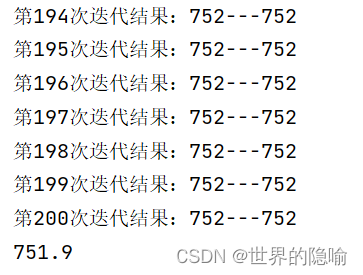
print("第{}次迭代结果:{}---{}".format(i, res_list[0], res_list[1]))
X.append(i)
Y.append(res_list[0])
init_data = change(init_data) # 基因交换
init_data = mata(init_data) # 基因变异
完整代码
'''
在一个长度为 n 的数组中选择 10 个元素,使得 10个元素的和 与 该元组中元素总和的 1/10 接近
'''
import random
import matplotlib.pyplot as plt
num_list_len = random.randint(10,100)
num_list = []
for i in range(num_list_len):
num = random.randint(1, 500)
while num in num_list:
num = random.randint(1, 500)
num_list.append(num)
# print(num_list_len, num_list)
# num_list_len = 78
#
# num_list = [35, 30, 52, 26, 18, 70, 56, 44, 74, 71, 38, 40, 31, 90, 98, 80, 78, 50, 16, 12, 14, 19, 76, 82, 79, 11, 33, 55, 37, 88, 73, 99, 72, 65, 29, 96, 66, 97, 54, 62, 100, 85, 61, 41, 20, 49, 13, 68, 51, 28, 86, 21, 34, 83, 63, 47, 64, 48, 46, 67, 10, 95, 58, 93, 59, 39, 94, 36, 87, 42, 84, 43, 22, 15, 17, 77, 24, 32]
#
def init(N):
"""
初始化染色体
:param N:
:return:
"""
init_data = []
for j in range(N):
init_list = []
for i in range(10):
rand_num = random.randint(0, num_list_len-1)
while num_list[rand_num] in init_list:
rand_num = random.randint(0, num_list_len-1)
init_list.append(num_list[rand_num])
init_data.append(init_list)
return init_data
def fitness(init_data):
"""
计算适应度
:param init_data: --> list
:param N: --> num
:return:
"""
fit_list = []
for i in range(len(init_data)):
sum_num = abs(sum(init_data[i])-sum(num_list)/10)
if sum_num == 0:
fit = 11
else:
fit = 1 / sum_num # fit 越高,适应度越高
fit_list.append((fit, i))
# print(fit_list)
return fit_list
def change(solve_list):
"""
PC = 0.7
:param solve_list: --> 染色体种群
:return: solve_list: --> 经过基因交换后的染色体种群
"""
# 选择父代列表和母代列表
male_list = solve_list[0::2]
female_list = solve_list[1::2]
# print(male, female)
for j in range(len(solve_list)):
# 选择需要交换基因的两个个体
# print(j)
if random.random() < 0.7:
male = male_list[random.randint(0, len(male_list)-1)]
female = female_list[random.randint(0, len(female_list)-1)]
# 两个个体之间的基因交换
random_index1 = random.randint(0, len(male)-1) # 要交换部分的起始索引点
random_index2 = random.randint(0, len(male)-1) # 要交换部分的末尾索引点
while random_index2 <= random_index1:
random_index1 = random.randint(0, len(male) - 1)
random_index2 = random.randint(0, len(male) - 1)
# child1, child2 = male[0:random_index1] + female[random_index1:random_index2] + male[random_index2:], female[0:random_index1] + male[random_index1:random_index2] + female[random_index2:]
child1_head = []
child1_tail = []
for i in male[0:random_index1]:
num = i
while num in female[random_index1:random_index2]:
num = male[random_index1:random_index2][female[random_index1:random_index2].index(num)]
child1_head.append(num)
for i in male[random_index2:]:
num = i
while num in female[random_index1:random_index2]:
num = male[random_index1:random_index2][female[random_index1:random_index2].index(num)]
child1_tail.append(num)
child1 = child1_head + female[random_index1:random_index2] + child1_tail
child2_head = []
child2_tail = []
# 子代2头
for i in female[0:random_index1]:
num = i
while num in male[random_index1:random_index2]:
num = female[random_index1:random_index2][male[random_index1:random_index2].index(num)]
child2_head.append(num)
# 子代2尾
for i in female[random_index2:]:
num = i
while num in male[random_index1:random_index2]:
num = female[random_index1:random_index2][male[random_index1:random_index2].index(num)]
child2_tail.append(num)
child2 = child2_head + male[random_index1:random_index2] + child2_tail
# print(len(set(child1)), len(set(child2)))
solve_list.append(child1)
solve_list.append(child2)
return solve_list
def mata(solve_list):
"""
基因突变
PM = 0.05 变异概率
:param solve_list: --> 染色体种群
:return: solve_list: --> 经过基因交换后的染色体种群
"""
for i in solve_list:
if random.random() < PM:
# print(i)
change_index = random.randint(0, len(i)-1)
rand_num = random.randint(0, num_list_len-1)
while num_list[rand_num] in i:
rand_num = random.randint(0, num_list_len - 1)
i[change_index] = num_list[rand_num]
solve_list.append(i)
# print(i)
return solve_list
def guiyi(init_data, fit_list):
"""
归一化处理以及染色体选择复制
:param init_data:
:param fit_list:
:return: init_data
"""
finally_data = []
# 适应度(可行解)排序
# print(init_data)
fit_list.sort()
fit_list = fit_list[::-1]
# print(fit_list)
index_list = [i[1] for i in fit_list]
init_data = [init_data[i] for i in index_list][0:N]
fit_list = fit_list[0:N]
# print(init_data)
# 概率归一化处理
num_list = [i[0] for i in fit_list]
P_list = [i / sum(num_list) for i in num_list] # 概率列表
P_guiyi_list = [P_list[0]] + [P_list[i] for i in range(1, len(P_list))] # 归一之后的概率列表
# 轮盘赌法染色体选择复制
for i in range(N):
P_num = random.random()
for j in range(len(P_guiyi_list)):
if P_num-j < 0:
finally_data.append(init_data[j])
break
return finally_data
N = 50 # 种群规模
T = 200 # 迭代次数
PM = 0.05 # 变异概率
PC = 0.7 # 交换概率
X = []
Y = []
init_data = init(N) # 初始化可行解
for i in range(T+1):
fit_list = fitness(init_data) # 计算适应度
init_data = guiyi(init_data, fit_list) # 轮盘赌法选择 N 规模的 可行解
# 输出迭代结果
fit_list = fitness(init_data)
fit_list.sort()
res_index_list = (max(fit_list)[1], min(fit_list)[1])
res_list = [sum(init_data[res_index_list[0]]), sum(init_data[res_index_list[1]])]
print("第{}次迭代结果:{}---{}".format(i, res_list[0], res_list[1]))
X.append(i)
Y.append(res_list[0])
init_data = change(init_data) # 基因交换
init_data = mata(init_data) # 基因变异
res = sum(num_list) / 10
print(res)
y = [res]* (T+1)
# print(x)
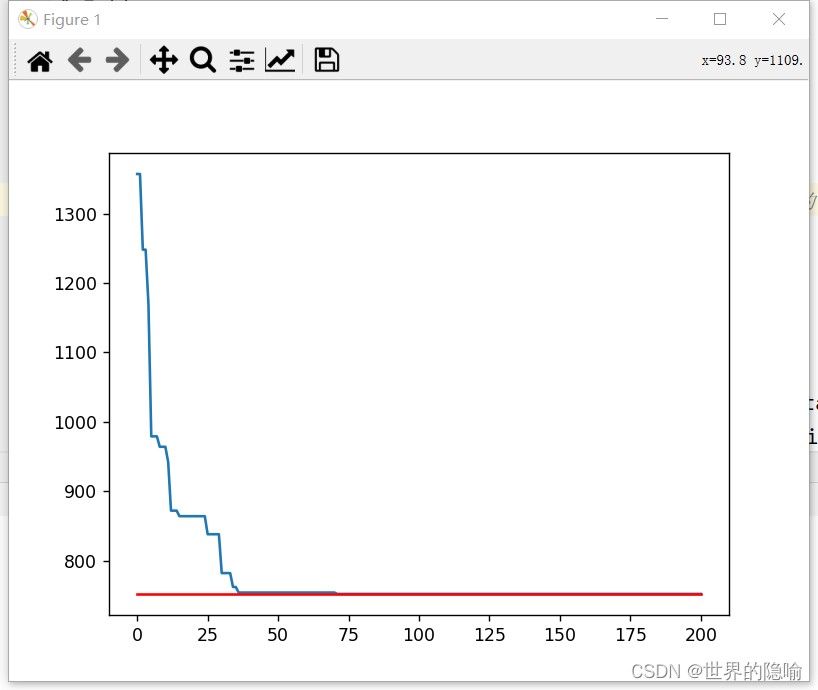
plt.plot(X, Y)
plt.plot(X, y,color='red')
plt.show()
运行结果