股价取对数之后的序列建模为随机游走。现在把取对数之后的股价当作是由一个随机游走和一个平稳时序组成：

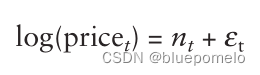
 是随机游走部分，是平稳部分。取对数后的股价求差就得到回报。所以在时间的回报表示为：

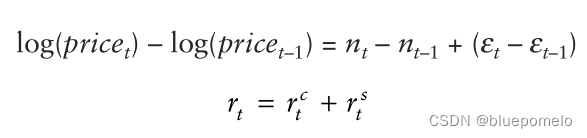
 表示非平稳部分的回报，表示平稳部分的回报。注意非平稳部分（趋势部分）的回报就是趋势的新息（innovation dervied from trend component)。所以，如果两个时间序列是协整的，那么从共同趋势得到的回报某种程度上（按照一定的比例）是相同的。那么到底为什么股票会有共同的回报（command return)呢?是否有金融方面的理论依据呢？是有的。套利定价理论正是提供了依据。

在APT中，股票的回报由共同因子回报（common factor return，我也想翻译成一般因子回报,即股票暴露在不同风险因子中得到的回报）和特定回报（specific return，股票的特定回报）组成。如果两个股票受到同样的风险因子的影响，那么两个股票的共同因子回报（common factor returns）是相同的。

根据APT,股票的回报由共同因子回报和特定回报组成。那么，APT中的共同因子回报对应共同趋势模型（common  trends model)中的共同趋势新息，APT中的特定回报对应共同趋势模型中的特定部分的一阶差分。这种对应成立的条件是，特定回报是平稳的时间序列。

我们说特定回报必须不是白噪声，但是APT模型不能保证特定回报时序是不是白噪声。因此，我们假设特定的回报序列不是白噪声。然而，令人放心的是，这一假设的有效性在进行协整测试时得到了检验，并且特定部分为非平稳的配对会被淘汰。

我们假设特定回报不是白噪声。我们就可以使用APT的术语去解释共同趋势模型的一些推论。新息序列的相关性就似乎共同因子的相关性。我们可以通过构造APT模型去估计共同因子方差以及协方差从而计算协整系数。

具有相同风险因素敞口（risk factor exposures风险因子暴露系数) 的一对股票是协整的必要条件。

我们看看两个条件：

 

 条件一，如果两个序列是协整的，它们从共同趋势得到的回报某种程度上（按照一定的比例）是相同的。

 

 

 条件二，如果两个股票是协整的，那么组合的价差跟从特定部分得到的价差是相同的。 此外，对于协整而言，价差序列必须是平稳的。如果特定价差是平稳的则价差是平稳的。如果两个股票的特定回报的整合起来的特定回报是平稳的，则特定价差是平稳的。这是我们将APT与协整联系起来时所做的假设。因此，如果这一假设成立，我们将满足所有协整的必要条件。

总结：

共同趋势模型把时间序列看成平稳和非平稳部分。注意，一般来说，在实际分析时间序列时，假设时序是由趋势(trend)部分、季节性部分（seasonal)、随机（stocahstic)部分组成。套利定价理论非常明确地表明了这种组合的观点，并采用了一种建构主义的方法来模拟股票收益。APT模型中的每个风险因素都与收益的时间序列相关。这些系列的加权求和，以因子敞口（factor exposure)作为权重，就是股票的预期回报序列。要获得实际回报，我们需要将特定的回报（specific return）序列添加到预期回报中。

两个股票如果由相同的风险因子敞口，它们将有相同的共同因子（common factor)回报。也就是说，长短投资组合（long-short portfolio)的共同因子回报是零（投资组合中两个股票的共同因子回报相互抵消了，因为一个买入，一个卖出）。此时，如果两个股票的特定回报的组合（the intergration of the specific returns of the stocks)是平稳的，那么这两个股票就是协整的。因此，寻找衡量协整性的方法的一个关键点是股票的风险因素敞口状况以及它们之间的关联程度。