给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

解题思路：

1.每个元素有选与不选两种情况，

2.回溯能将选与不选这两种情况都包含

3.递归刚好能满足这个需求

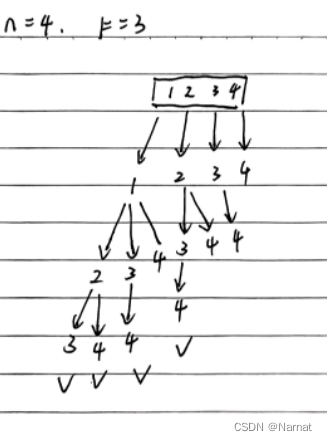
dfs + 回溯代码：

class Solution {
    public List<List<Integer>> combine(int n, int k) {
           List<List<Integer>> end = new ArrayList<>();
           List<Integer> mb = new ArrayList<>();
           
        	   addmbzh(1, k, end, mb, n);
           
           return end;
    }
    public static void addmbzh(int x, int k, List<List<Integer>> end, List<Integer> none, int n) { 
        if(x > n + 1) return;
    	if(none.size() == k) {
        end.add(new ArrayList<Integer>(none));
        return;
        }
        none.add(x);
        addmbzh(x + 1, k, end, none, n);
    	none.remove(none.size() - 1);
    	addmbzh(x + 1, k, end, none, n);
    }
}

可以出上述递归树，有很多没有用的分支，可以加入特定判断条件将无用分支剪切掉

if(none.size() + n - x + 1 < k) return;//即剩下元素不足，直接退出

dfs + 回溯 + 剪枝：

class Solution {
    public List<List<Integer>> combine(int n, int k) {
           List<List<Integer>> end = new ArrayList<>();
           List<Integer> mb = new ArrayList<>();
           
        	   addmbzh(1, k, end, mb, n);
           
           return end;
    }
    public static void addmbzh(int x, int k, List<List<Integer>> end, List<Integer> none, int n) { 
        if(none.size() + n - x + 1 < k) return;//退出条件
    	if(none.size() == k) {
          end.add(new ArrayList<Integer>(none));
          return;
        }
        none.add(x);//选
        addmbzh(x + 1, k, end, none, n);
    	none.remove(none.size() - 1);//回溯（不选）
    	addmbzh(x + 1, k, end, none, n);
    }
}

不难看出爆搜会超时的主要原因是一些无用枝节耗费了大量时间

本代码也可以用全局变量来写，反而更简洁

代码：

class Solution {
    List<List<Integer>> nums = new ArrayList<>();
    List<Integer> num = new ArrayList<>();
	public List<List<Integer>> combine(int n, int k) {
           dfs(1, n, k);
           return nums;
	}
	public  void dfs(int i, int n, int k) {
		if(num.size() + n - i + 1 < k) return;//剪枝
		if(num.size() == k) {
		  nums.add(new ArrayList<Integer>(num));
		  return;
		}//重要的事情最先做
		
		num.add(i);//装
		dfs(i + 1, n, k);
		num.remove(num.size() - 1);//回溯（不装）
		dfs(i + 1, n, k);
	}
}