• 这三道题目都属于物品数组里没有分开重量和价值，我们令重量=价值的类型，这种类型背包问题很常见。
• 也就是给出一个数组nums[i]，判断nums[i]里能不能找出子集，令子集元素总和=某特定目标值。前两道题是能否找出子集，即能否填满背包；最后一题是找所有符合条件子集的个数，也就是填满背包的方案数目。
• 填满背包这个概念就是物品价值=重量的时候才有，因为背包问题推导的是物品的最大价值，且背包问题限制是背包最大重量为j。当价值=重量的时候，最大价值=最大重量<=背包容量j，才能对填满背包的情况进行分析。

416.分割等和子集（回溯+01背包）

给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1：

输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：

输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

思路

本题目的是把集合分成两个子集，使得分出来的两个子集的和相等。如果两个子集元素和相等，也就说明他们的和都是集合元素总和的一半。

这道题目本质就是，例如集合总和为22，此时找出集合内有哪些元素相加=11，剩下的元素相加自然也=11.

回溯解法（类似组合总和Ⅱ）

本题本质上是求解集合内是否存在子集，其总和=sum/2，也就是总和是否=target。。这个问题看起来很像 39.组合总和 系列的问题。组合总和题目如下：

40.组合总和Ⅱ

组合总和Ⅱ对应写法：

class Solution {
public:
    void backtracking(vector<int>&path,vector<vector<int>>&result,vector<int>& candidates,int sum,int target,vector<int>&used,int startIndex){
        //终止条件
        if(sum>target){
            return;
        }
        if(sum==target){
            result.push_back(path);
            return;
        }
        //单层搜索
        for(int i=startIndex;i<candidates.size();i++){
            //防止访问下标-1越界，涉及到下标-1的都必须检查越界问题
            if(i>=1&&candidates[i]==candidates[i-1]&&used[i-1]==0){
                continue; //直接不处理，跳到for循环的下一个
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            //记录use过当前的i
            used[i]=1;
            //开始递归
            backtracking(path,result,candidates,sum,target,used,i+1);
            //回溯，重置use
            sum -= candidates[i];
            path.pop_back();
            used[i]=0;
        }
    }
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
		vector<int>path;
        vector<vector<int>>result;
        //注意这种带有初始大小和初始值的vector数组定义方式！需要访问used下标所以必须初始化
        vector<int>used(candidates.size(),0);
        int sum=0;
        int startIndex=0;
        sort(candidates.begin(),candidates.end());
        backtracking(path,result,candidates,sum,target,used,startIndex);
        return result;
    }
};

我们可以通过修改 “组合总和II” 的回溯方法来解决 “将数组分割成两个子集，使得两个子集的元素和相等” 这个问题。

按照组合总和Ⅱ的思路，本题的回溯写法如下：

• 本题与组合总和II的主要区别在于我们在找到一个符合条件的组合后就直接返回，不再继续搜索，因为我们只关心是否存在这样的组合，而不关心有多少种组合。

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        // 计算数组所有元素之和
        int sum = accumulate(nums.begin(), nums.end(), 0);
        // 如果和不是偶数，无法平分，直接返回false
        if (sum % 2 != 0) {
            return false;
        }
        // 平分数组的目标和
        int target = sum / 2;
        // 对数组进行排序，有利于后续剪枝
        sort(nums.begin(), nums.end());
        // 初始化一个记录使用状态的数组
        vector<int> used(nums.size(), 0);
        // 从数组开始处开始进行回溯寻找
        return backtrack(nums, target, 0, used);
    }

    bool backtrack(vector<int>& nums, int target, int start, vector<int>& used) {
        // 如果target减为0，表示已经找到一组符合条件的子集，返回true
        if (target == 0) {
            return true;
        }
        // 开始单层搜索
        for (int i = start; i < nums.size(); ++i) {
            // 防止访问下标-1越界，涉及到下标-1的都必须检查越界问题
            // 直接跳过连续的、相同的元素，防止产生重复的子集
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == 0) {
                continue; //直接不处理，跳到for循环的下一个
            }
            // 剪枝：如果当前数字大于target，后续无需再进行，直接break
            if (nums[i] > target) {
                break;
            }
            // 做选择，将当前元素纳入子集，和减少nums[i]
            used[i] = 1;
            // 继续递归填充子集，如果找到一组，直接返回true
            if (backtrack(nums, target - nums[i], i + 1, used)) {
                return true;
            }
            // 撤销选择，回溯，恢复状态
            used[i] = 0;
        }
        // 当前没有找到符合条件的子集，返回false
        return false;
    }
};

回溯解法存在的问题

这种解法思路是正确的，可以通过小用例，但是大用例会超时。通过这道题我们也可以复习一下组合总和系列的回溯解法。

应该可以用记忆型搜索来优化，但是暂时不做尝试，后面再补充优化。

01背包思路

背包问题，是有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

背包问题有多种背包方式，常见的有：01背包、完全背包、多重背包、等等，要注意题目描述中商品是不是可以重复放入。

即一个商品如果可以重复多次放入是完全背包，而只能放入一次是01背包，写法是不一样的。

首先要明确，本题中我们要使用的是01背包，因为元素我们只能用一次。

为什么能抽象成背包问题

首先，本题要求集合里能否出现总和为 sum / 2 的子集。

01背包问题的一种应用是，只看背包是否能够正好装满，不在意背包的最大价值，也可以不在乎物品的价值，只看重量。

确认了以下四点，才能把01背包套到本题上面来。

• 背包的最大重量为sum / 2
• 背包要放入的商品（集合里的元素）重量为元素的数值，（价值也为元素的数值，可以直接令价值=数量，也可不考虑价值）
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素不可重复放入。

01背包写法1：常规写法，考虑重量=价值

重量=价值类问题的思考方式

首先明确一点，我们不可能放入总重量>背包容量的物品。

因为01背包问题的递推公式是：

for(int i = 0; i < nums.size(); i++) {
    for(int j = target; j >= nums[i]; j--) { 
        dp[j] = max(dp[j], dp[j - weight[i]] +value[i]);
    }
}

这个公式的意思是，如果我要在背包容量为 j 的情况下，尝试放入第 i 个物品（weight[i]），那么我首先要保证我的背包容量 j 大于等于我要放入的物品的重量weight[i]。也就是 j >= weight[i]。

这个限制，确保了我们不能在背包容量小于物品重量的情况下将物品放入背包，也就避免了总重量大于背包容量的情况。

当物品重量=价值的时候，也就是说，物品的最大价值dp[j]，也就是他的最大重量。而根据上面推导得知，背包最大重量一定是小于容量j的。也就是说，如果背包想要装满，那么他的最大重量dp[j]需要满足dp[j]=j。

因此，对于这种重量=价值的背包问题，判断背包装满的方法就是， dp[target]==target的时候，就说明背包装满了。

DP数组含义

01背包中，dp[j]表示，容量为j的时候，背包的最大价值是dp[j]。

本题每个元素重量=价值，也就是说，如果我们把容量为11的背包装满，他的价值应该也是11。按照上面重量=价值问题的分析思路，如果dp[j]=j，说明背包刚好装满了。（实际上最大价值=j，就说明最大重量达到j了，就说明装满了）

递推公式

01背包的一维递推公式是：

dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);//dp[j]由二维DP数组压缩得到，压缩了dp[i-1]

在本题中，weight[i]和value[i]是相等的，都是数值nums[i]

因此递推公式为：

dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);

DP数组初始化

dp[0]=0，容量为0的背包所装价值最大为0。

因为涉及到最大值的取值，因此其余非0下标全部初始化为0。

遍历顺序

本题遍历顺序就是01背包的遍历顺序，也就是物品在外，背包在内，且背包为倒序遍历。（因为每个物品只有一个）

//一维DP遍历顺序不可颠倒，二维DP可以
for(int i=0;i<nums.size();i++){
    //背包容量为目标值target
    for(int j=target;j>=nums[i];j--){
        //递推公式
        dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);
    }
}

写法1完整版

• 注意，DP数组含义是容量为j的时候，dp[j]代表最大价值（最大重量）。定义DP数组的时候，j的最大值也就是最大容量，也就是vector<int>dp(target+1,0)（每个用例的target都不一样，这样不会发生越界错误）

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum=0;
        //先计算总和，如果是奇数直接返回
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
        }
        if(sum%2!=0) return false;//奇数不可能分成相等两部分
        
        int n=nums.size();
        int target=sum/2;
        
        //创建一维DP数组
        vector<int>dp(n+1,0);
        for(int i=0;i<n;i++){
            for(j=target;j>=nums[i];j--){
                dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        if(dp[target]==target){
            return true;
        }
        return false;
    }
};

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)

debug测试

最开始的时候发生了越界错误，原因是一维DP数组大小设置成了nums.size()，也就是物品个数。实际上这是错误的，dp[j]中j的含义是背包容量，DP数组的大小应该设置为背包容量j的最大值。

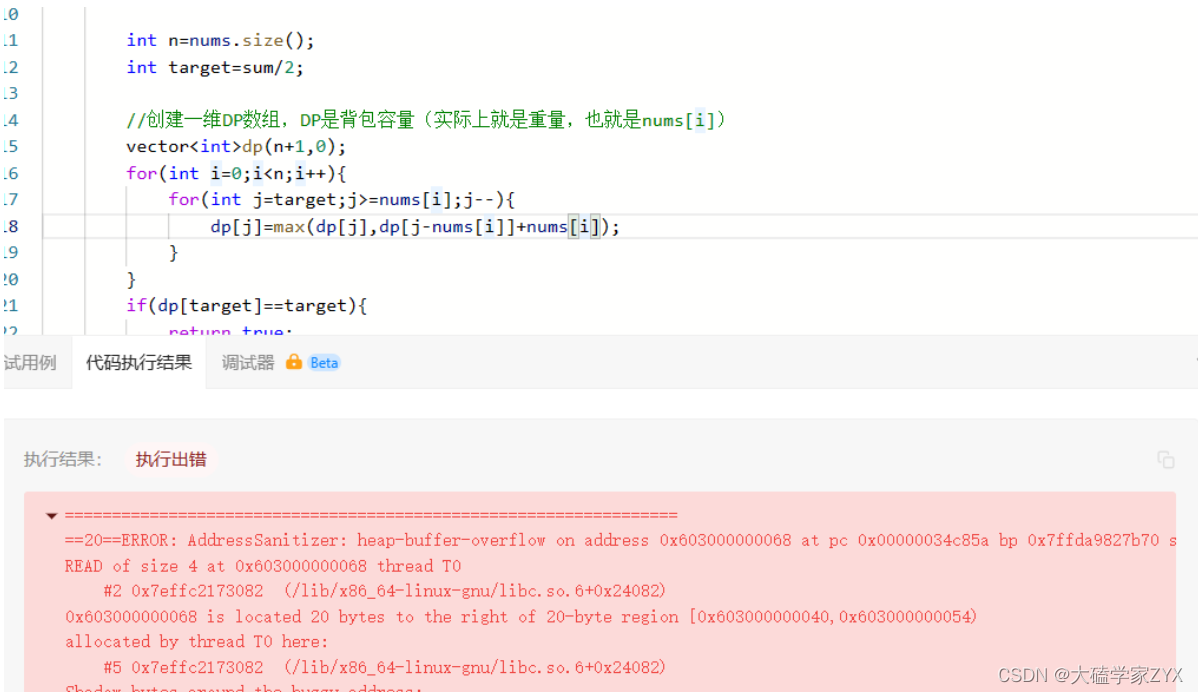
背包容量j是从target开始倒序遍历，因此DP数组大小改为vector<int>dp(target+1,0)即可。

01背包写法2：只看能否装满重量，不考虑价值的写法

这个问题实际上也可以抽象为一个只考虑重量的01背包问题，也就是集合有若干已知重量的物品，问容量为sum/2的背包能不能刚好装满。不考虑背包对应的价值，重新写一个递推公式。

DP数组含义

我们采用一维DP的01背包思路来解决，如果不考虑价值只考虑重量，那么dp[j]数组的含义是，能否通过选取数组中的一些数，使得这些数的和等于 j。

背包装满的条件是：存在一个子集，它的和等于背包的容量target。这个条件可以通过检查dp[target]是否为真来判断。

递推公式

结合DP数组的含义，我们对于每一个dp[j]，需要判断能不能选取数组数字，使得数字之和（也就是物品重量之和）是j。

因此，我们在遍历过程中，可以让dp[0]=0，因此

dp[j]=dp[j]||dp[j-nums[i]]

这个递推公式也可以写成：

for (int i = 0; i < n; ++i) {
   for (int j = target; j >= nums[i]; --j) {
       if(dp[j-nums[i]]==true){
          dp[j]=true;
        }
   }
}

为什么这样写能收集所有和为target的情况

当我们在数组中遍历到元素nums[i]时，若dp[j - nums[i]]为真，说明我们能在数组中选取若干元素，使得他们的和等于j - nums[i]。而这时如果我们再加上当前的元素nums[i]，总和就会变成j - nums[i] + nums[i] = j。这就说明存在一个子集，他们的和等于j，所以我们可以更新dp[j] = true。

举个例子，假设我们在遍历数组时，当前元素nums[i] = 5，我们希望找到和为11(target)的子集，即j = 11。这时，j - nums[i] = 11 - 5 = 6。若dp[6]为真，说明我们已经找到了和为6的子集。那么如果我们再加上当前的元素5，和就变成了6 + 5 = 11，所以我们就找到了和为11的子集，于是我们可以更新dp[11] = true。

初始化

这种做法的思路是，遍历过程中通过判断dp[j-nums[i]]是否为真，nums[i]为当前物品的重量，我们在初始化的时候令dp[0]=true，其他全部为false，那么只有满足j=nums[i]（也就是刚好装得下）的时候，dp[j]才会变成true。

因此初始化方式是，dp[0]=true，其他全部为false。

写法2完整版

对于每个数字nums[i]，从target到nums[i]进行逆序遍历。如果dp[j - nums[i]]为真，说明存在一个子集，它的和为j - nums[i]。那么加上nums[i]之后，和就变成了j，所以此时可以将dp[j]更新为true。

• 集合有若干已知重量的物品，问容量为sum/2的背包能不能刚好装满。

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        int totalSum = accumulate(nums.begin(), nums.end(), 0);
        int target = totalSum / 2;
        if (totalSum % 2 == 1) return false;
        vector<bool> dp(target + 1, false);
        dp[0] = true;
        for (int i = 0; i < n; ++i) {
            for (int j = target; j >= nums[i]; --j) {
                if(dp[j-nums[i]]==true){
                    dp[j]=true;
                }
            }
        }
        return dp[target];
    }
};

总结

这道题目就是一道01背包应用类的题目，需要我们拆解题目，然后套入01背包的场景。

01背包相对于本题，主要要理解，题目中物品是nums[i]，重量是nums[i]，价值也是nums[i]，背包体积是sum/2。

第一种写法是重量=价值的写法，相对来说好理解一些。需要注意的一点就是重量=价值，那么dp[j]代表的最大价值，一定<=j（最大重量），因为背包问题的大前提就是，放入背包的所有物品最大重量一定<=背包容量。

1049.最后一块石头的重量

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

示例 1：

输入：stones = [2,7,4,1,8,1]
输出：1
解释：
组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

示例 2：

输入：stones = [31,26,33,21,40]
输出：5

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 100

背包思路

本题的主要思路就是，尽量找重量相同的石头，才能让最后剩下的重量最小。也就是要让石头分成重量相等的两堆。

这个思想其实就和416.分割等和子集问题很像了，找一个容量是sum/2的背包，先把石头装满两个背包，剩下要么为0，要么还有剩余（sum不能整除2还有余数），此时剩余就是最小石头。

我们可以把石头分成两组 x 和 y，有x + y = sum。

我们假设 x <= y，那么我们希望 x 和 y尽可能接近，所以 x 越大越好。但是 x 最大也只能是 sum / 2，因为它比 y 小。

所以，我们如果想让x和y尽可能接近，就是看 sum / 2 最多能装的价值是多少，sum / 2最多能装的价值，就是x的数值。

DP数组含义

本题因为每个石头只有一个，所以属于01背包问题。同时本题也是物品重量=价值的类型，和 416.分割等和子集 很像。

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。

相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，最多可以装的价值为 dp[j] == 最多可以背的重量为dp[j]

递推公式

本题递推公式和上一题一样，都是为了装满，因此dp[j]仍然是最大重量/最大价值。

dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);

DP数组初始化

本题dp[0]代表装满容量0的最大价值，dp[0]=0。

因为其他也涉及max的对比，所以所有初始值都设置成0.

遍历顺序

遍历顺序同01背包遍历顺序。

完整版

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        //先求总和sum
        int sum=0;
        for(int i=0;i<stones.size();i++){
            sum+=stones[i];
        }
        int target = sum/2;//向下取整即可，这里不需要整除
        //定义DP数组
        vector<int>dp(target+1,0);
        //不需要单独初始化
        for(int i=0;i<stones.size();i++){
            for(int j=target;j>=stones[i];j--){
                dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        //总和减去两个背包就是剩下的最小石头
        int left = sum-dp[target]-dp[target];
        return left;

    }
};

这两个背包都是装满的状态吗？

不一定，这个解决方案并不是要求两个背包都必须装满，而是尽可能让这两个背包的重量接近。在这种情况下，可能会有剩余的石头，这些就是剩下的石头的重量。dp[j]表示背包容量为j时能装的石头的最大重量。而最后的结果是sum - 2 * dp[target]，这里的sum是所有石头的总重量，dp[target]表示能够装满容量为sum/2的背包的石头的最大重量，即两个背包的重量和。

此时，sum - 2 * dp[target]就表示剩下的石头的重量，也就是我们要求的答案。

总结

本题其实和 416. 分割等和子集 几乎是一样的，只是最后对dp[target]的处理方式不同。

416. 分割等和子集 相当于是求背包是否正好装满，而本题是求背包最多能装多少。

494.目标和（递推公式重点:方案数问题模板）

给你一个整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个 表达式 ：

例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

背包写法思路

本题最重要的是推导过程，以及为什么能套用01背包。

题目要求在数字前面加+或者-，求出经过正负赋值之后，数组总和运算结果等于 target 的不同表达式的数目，也就是求方案数目。

也就是说会出现一批正数和一批负数。我们假设所有正数的和为x，所有负数（目前还是正整数的状态）的和为y。可以列出如下式子：

• x+y=Sum
• x-y=target

可以得出x=(Sum+target)/2。

由于x是正数的和，因此我们此时就可以把问题转换为背包问题，也就是总容量为x的背包，物品从nums[i]里面抽取，要求正好装满这个容量为x的背包，共有多少组nums[i]？

本题和前几道题一样，都属于物品重量=价值类型的题目（因为数组内只有单一数字），也就是属于规定一个目标和target，看数组nums[i]里有没有加起来总和刚好等于目标值的子集/有多少个总和刚好=target的子集的问题。

(target + sum) / 2 向下取整的影响

由上一道石头的题目我们也可以知道，/2的操作如果除不尽，是向下取整的。例如5/2=2。

但是实际上，本题向下取整并没有影响，因为**(target + sum)如果是奇数，说明x和y是无解的**。本题要求的就是x和y，无解没有意义。

同时，如果sum值已经<target，也是一定无解的。

限制条件

由上面的分析可以得到两个限制：

• 原数组sum值<target无解，注意target需要是绝对值，因为target有可能是负数！
• (target+sum)是奇数无解

if(sum<abs(target)) return 0;
//这里注意target需要是绝对值，因为target有可能是负数！
if((target+sum)%2!=0) return 0;

DP数组含义

本题和之前遇到的两道题不太一样，虽然都属于物品重量=价值的情况，但是之前都是求容量为j的背包，装满的时候是什么情况。

本题则是装满有几种方法，求方案数目。其实这就是一个组合问题了。

在这个组合问题中，dp[j] 表示：填满j（包括j）这么大容积的包，有dp[j]种方法。

递推公式（组合问题/求方案数问题的递推公式模板）

dp[j]表示填满j（包括j）这么大容积的包，有dp[j]种方法。

在遍历中，我们先是知道i从0到n的所有取值，再针对每个i的取值，对所有的背包容量j进行遍历。也就是说，我们只要知道nums[i]的值，凑成dp[j]就有dp[j - nums[i]] 种方法。

例如：dp[j]，j 为5，

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
• 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。也就是相当于，把背包问题每一个i对应的DP数组，dp[j]这个位置上的所有数值，都进行累加！

类似下图的情况，dp[5]的所有方案，是所有物品都遍历完，都考虑在内之后的累加总和。

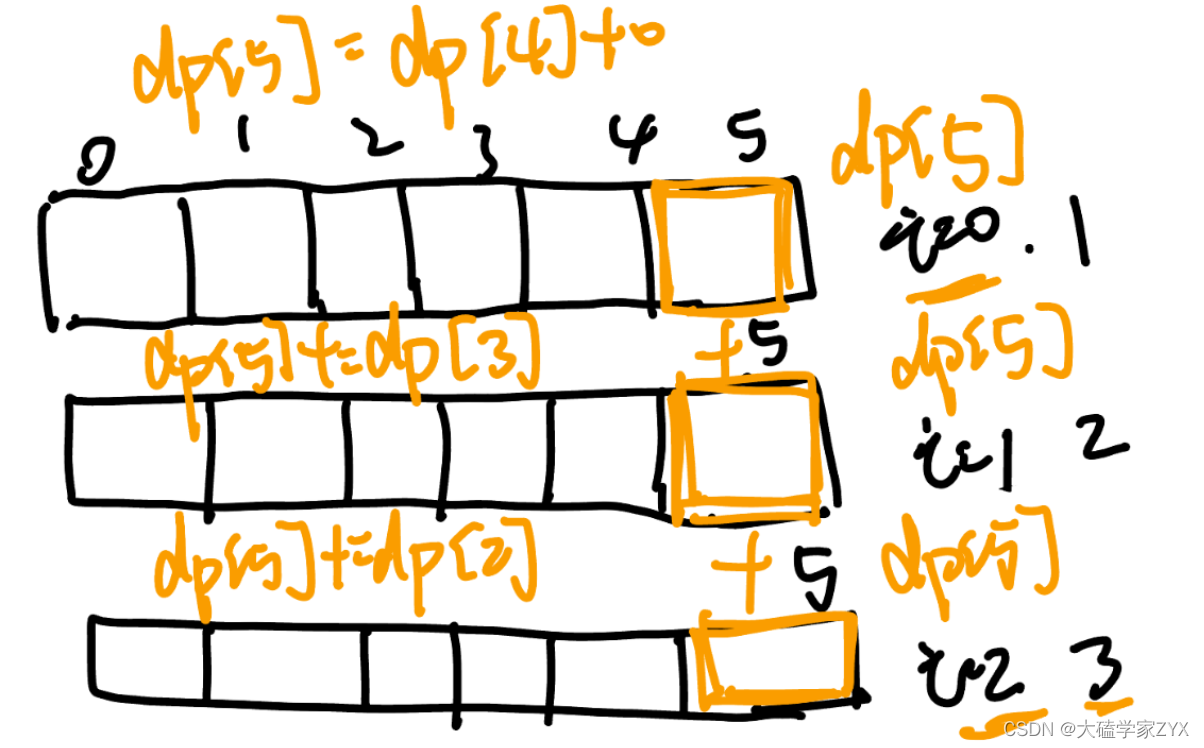
所以，求组合类/方案数目问题的公式，都是类似这种：

dp[j]+=dp[j-nums[i]];

DP数组初始化（重要）

组合问题/求方案数问题，初始化非常重要，因为方案数递推公式的推导，全部都是基于dp[0]进行的。

本题dp[0]含义是背包容量为0的时候，有多少种方案。我们直接把dp[0]代入递推公式，从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

代入数组j=0的情况，如果数组[0] ，target = 0，那么 x= (target + sum) / 2 = 0。 此时dp[0]也应该是1， 也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。

所以本题我们应该初始化 dp[0] 为 1。

遍历顺序

本题的物品不能重复使用，是划分子集类的问题，因此属于01背包。01背包的遍历顺序是物品在外，背包容量在内，且背包容量倒序遍历。

完整版

class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        //首先排除无解的情况
        int sum=0;
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
        }
        int totalSum = sum+target;
        //如果是奇数，没有x
        if(totalSum%2!=0) return 0;
        //如果原数组sum<target绝对值，必然无解
        if(sum<abs(target)) return 0;
        
        int x=totalSum/2;//背包最大容量
        //定义DP数组
        vector<int>dp(x+1,0);
        //初始化dp[0],这一步在方案数问题很重要
        dp[0]=1;
        for(int i=0;i<nums.size();i++){
            for(int j=x;j>=nums[i];j--){
                dp[j] += dp[j-nums[i]];
            }
        }
        //dp[x]就是方案数目
        return dp[x];

    }
};

• 时间复杂度：O(n × m)，n为正数个数，m为背包容量
• 空间复杂度：O(m)，m为背包容量

总结

实际上，回溯算法：39. 组合总和 的系列问题，也可以用dp来做，如果仅仅是求所有组合个数的话，用dp比用回溯节省很多时间。

但回溯算法：39. 组合总和 (opens new window)要求的是把所有组合都列出来，还是要使用回溯法爆搜的。

可以作为模板记住，在求装满背包有几种方法的情况下，递推公式一般为：

dp[j] += dp[j - nums[i]];

完全背包还会用到这个递推公式。