104. 二叉树的最大深度

思路：这道题推荐用层序遍历递归的方式

递归三要素：

                终止条件：当当前node为空时候 

                单层递归逻辑：分别向node的左子树和右子树进行递归，定义left和right接受返回值

                递归参数：root

代码：

def maxDepth(self, root: Optional[TreeNode]) -> int:
        return self.count_depth(root)



    def count_depth(self,node):
        if not node:
            return 0 
        left =self.count_depth(node.left)
        right = self.count_depth(node.right)
        return max(left,right)+1

111. 二叉树的最小深度

 

 思路：这道题依旧是是用层序遍历的方式，不得不说层序遍历真的很好用！！！

不过这里会多几个判断条件，定义left&right去接受左子树和右子树的高度之后。

判断当前root的左右子树是否为空

if node.left==None and node.right!=None:
            return 1+right
        elif node.left==None and node.right==None:
            return 1 
        elif node.left!=None and node.right==None:
            return 1+ left
        else:
            return min(left,right)+1

这也是这道题的核心部分。

递归三要素：

                终止条件：当node为空时返回0 

                递归参数:root就足够了

                单层递归：就是当前node的左孩子和右孩子

代码：

         

def minDepth(self, root: Optional[TreeNode]) -> int:
        return self.depth(root)

    def depth(self,node):
        if not node:
            return 0 
        left = self.depth(node.left)
        right = self.depth(node.right)
        if node.left==None and node.right!=None:
            return 1+right
        elif node.left==None and node.right==None:
            return 1 
        elif node.left!=None and node.right==None:
            return 1+ left
        else:
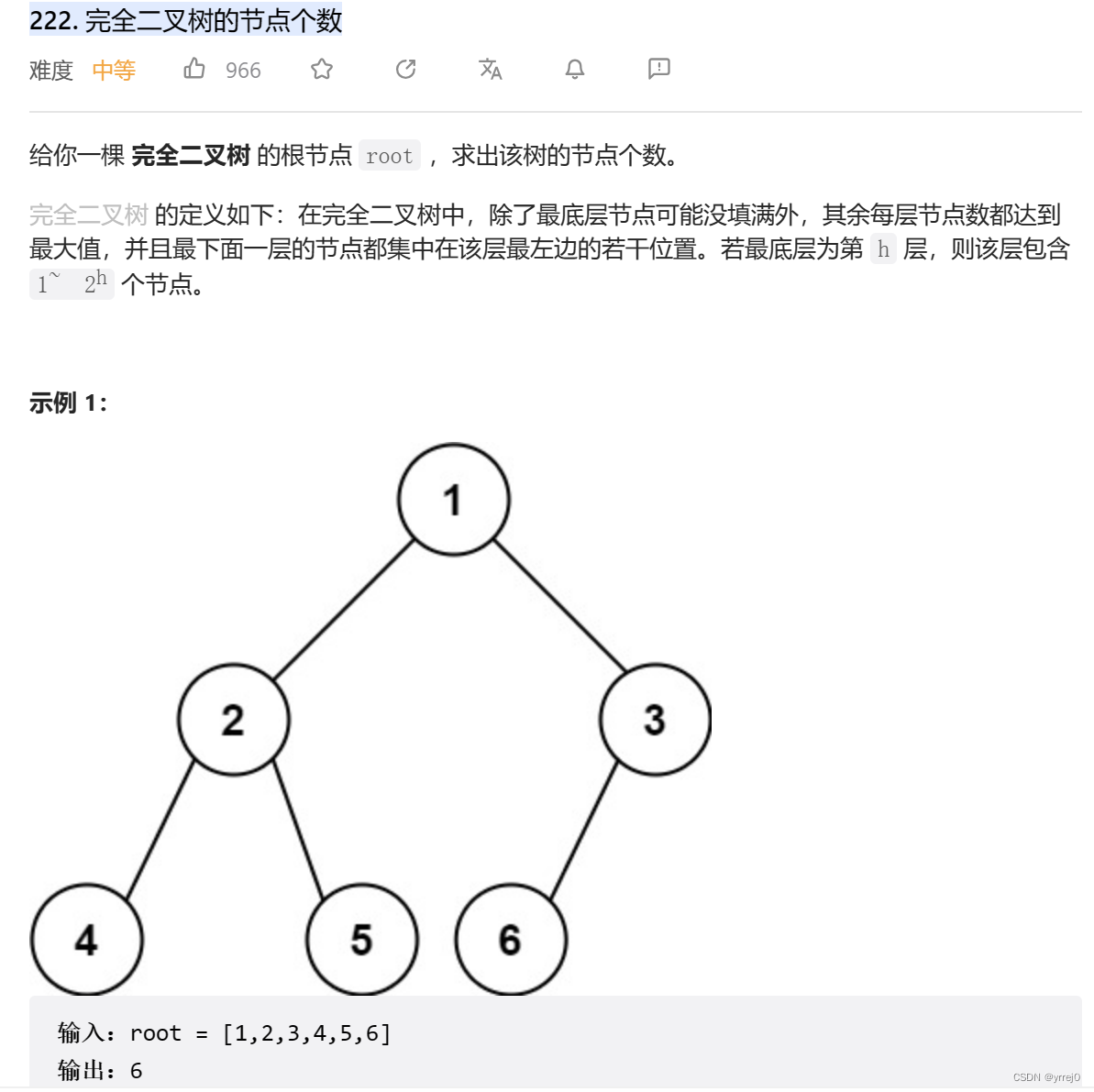
            return min(left,right)+1

222. 完全二叉树的节点个数

 

思路：      

1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回以该节点为根节点二叉树的节点数量，所以返回值为int类型。
2. 确定终止条件：如果为空节点的话，就返回0，表示节点数为0。
3. 确定单层递归的逻辑：先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量
4. 代码：

   def countNodes(self, root: Optional[TreeNode]) -> int:
           return self.count(root)
   
   
       def count(self,node):
           if not node:
               return 0 
           left = self.count(node.left)
           right = self.count(node.right)
           return left+right+1