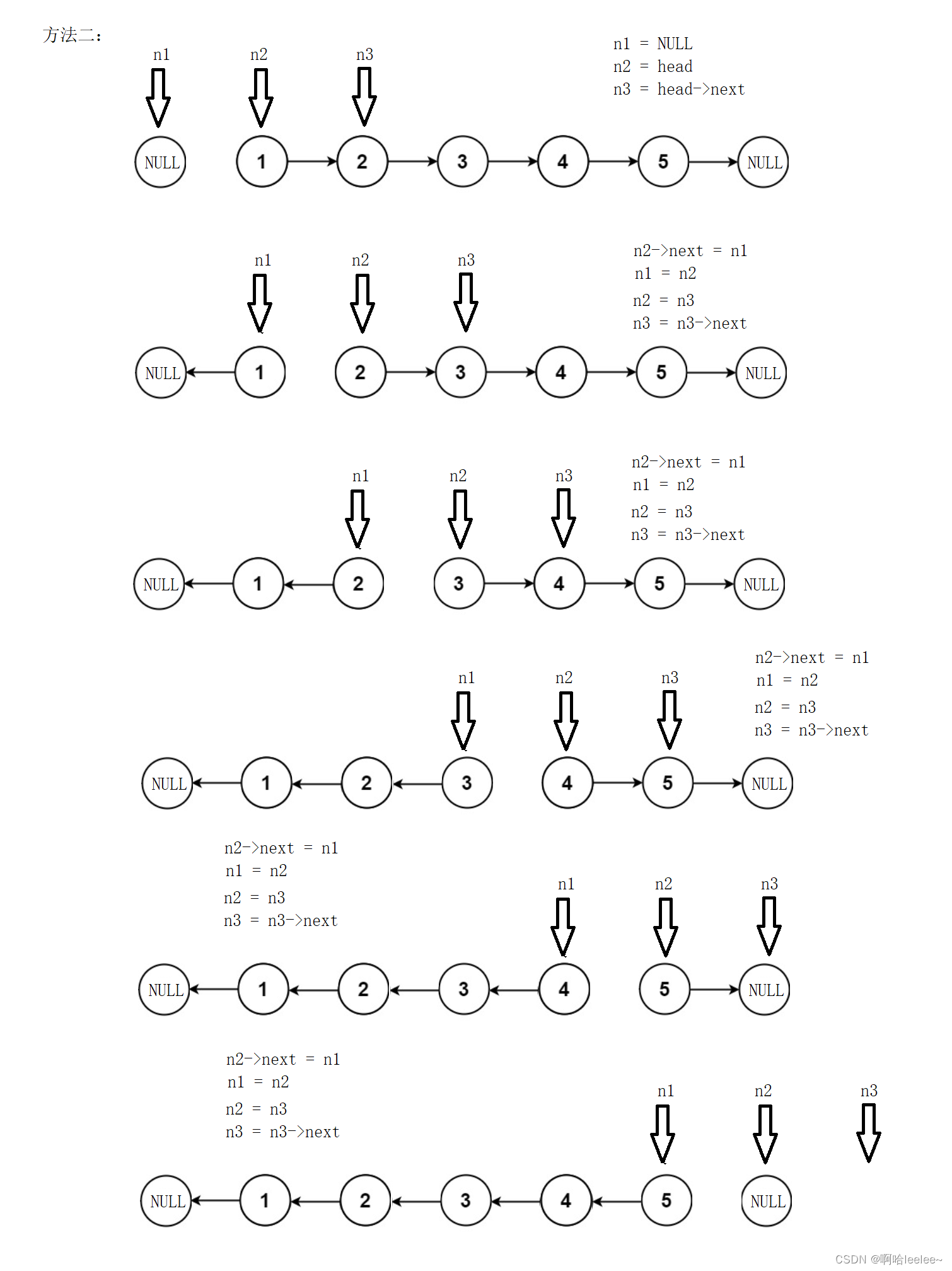
概念：

编辑距离，由俄罗斯科学家Vladimir Levenshtein于1965年提出，因此又称为Levenshtein Distance，简称LD，是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。

可用的编辑操作包括：
- 将某个字符替换为另一个字符
- 插入字符
- 删除字符

Levenshtein Distance公式定义：

将两个字符串 a, b 的Levenshtein Distance表示为LDa,b(|a|, |b|)，如下公式所示。其中，|a|和 |b|分别对应字符串 a, b 的长度。
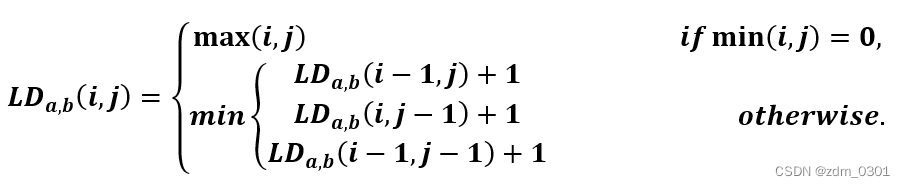
在这里插入图片描述
LDa,b(|a|, |b|)表示 a 的前 i 个字符与 b 的前 j 个字符之间的编辑距离。其中，i 和 j 都是从1开始的下标。

示例一（不等长字符串）：

将字符串Kitten转换成字符串Sitting

1. Kitten —> Sitten（K —> S）
2. Sitten —> Sittin （e —> i）
3. Sittin —> Sitting (在末尾插入字符‘g’)

将Kitten转换成Sitting的LD值为3。

示例二（等长字符串）：

将字符串hello转换成字符串kitty

1. hello —> kello（h —> k）
2. kello —> killo（e —> i）
3. killo —> kitlo（l —> t）
4. kitlo —> kitto（l —> t）
5. kitto —> kitty（o —> y）

将hello转换成Sitting的LD值为5。

代码实现：

def edit_distance(a, b):
    m, n = len(a), len(b)
    if m == 0:
        return n
    if n == 0:
        return m
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    for i in range(m + 1):
        dp[i][0] = i
    for j in range(n + 1):
        dp[0][j] = j
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + (s1[i - 1] != s2[j - 1]))
    # print(dp)
    return dp[m][n], 1 - dp[m][n] / m