逻辑回归：从理论到实践

在本文中，我们将介绍一种被广泛用于二分类问题的机器学习模型——逻辑回归。我们将通过一个实例，深入解析如何在 Python 环境中实现逻辑回归。

源数据下载链接

1. 什么是逻辑回归？

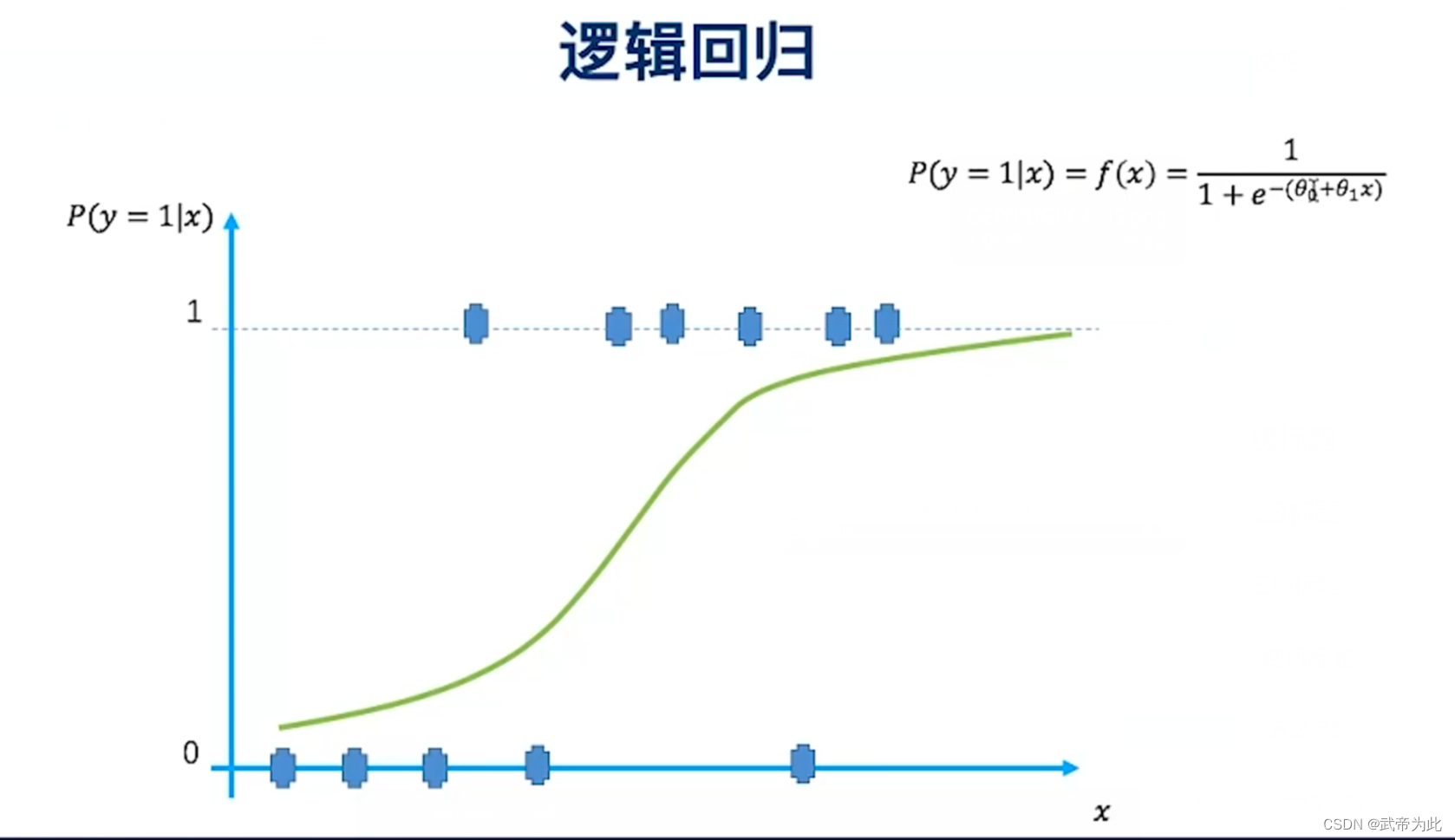
逻辑回归是一种用于解决二分类问题的监督学习模型。它的主要思想是：首先将输入特征与线性回归模型相结合，然后将线性回归的输出通过一个称为 sigmoid 函数的特殊函数转换，使得其输出值落在 (0, 1) 之间，代表了正类的概率。具体地，逻辑回归模型的形式可以表示为：

其中，(P(Y=1|X)) 是在给定输入特征 (X) 的情况下，目标变量 (Y) 为正类的概率；(w_0, w_1, …, w_n) 是模型需要学习的参数；(X_1, X_2, …, X_n) 是输入特征。这个方程的右侧部分就是 sigmoid 函数，其图像是一个 S 形曲线，可以将任何实数映射到 (0, 1) 之间。

2. Python 实现逻辑回归：

接下来，我们将通过一个完整的例子来展示如何在 Python 中实现逻辑回归模型。

2.1 数据预处理

在进行机器学习模型的训练之前，我们首先需要对数据进行预处理。在这个例子中，我们使用了一个名为 “bank-full.csv” 的数据集。这个数据集包含了一些银行客户的信息，以及他们是否订阅了定期存款（这是我们的目标变量，用 “y” 表示）。

首先导入了所需的库，并读取数据集：

import pandas as pd
import numpy as np
from sklearn import preprocessing
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import seaborn as sns

sns.set(style='white')
sns.set(style='whitegrid', color_codes=True)

data = pd.read_csv('bank-full.csv', sep=';', quotechar='"', header=0)
data.dropna(inplace=True)
print(data.head())
print(data.shape)
print(list(data.columns))

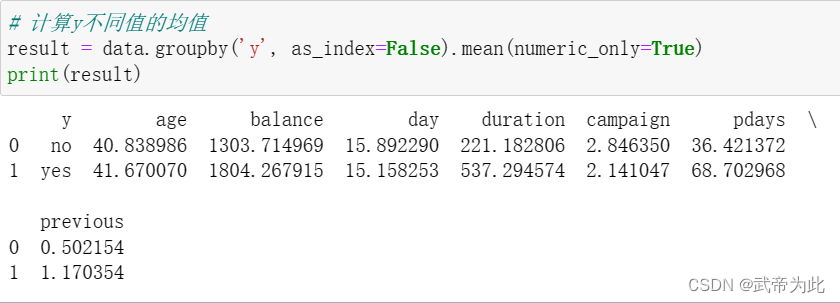
然后，我们对数据集中的每个属性的所有可能值进行了查询：

data['education'].unique()
print("education的所有可能值：")
print(data['education'].unique())
...

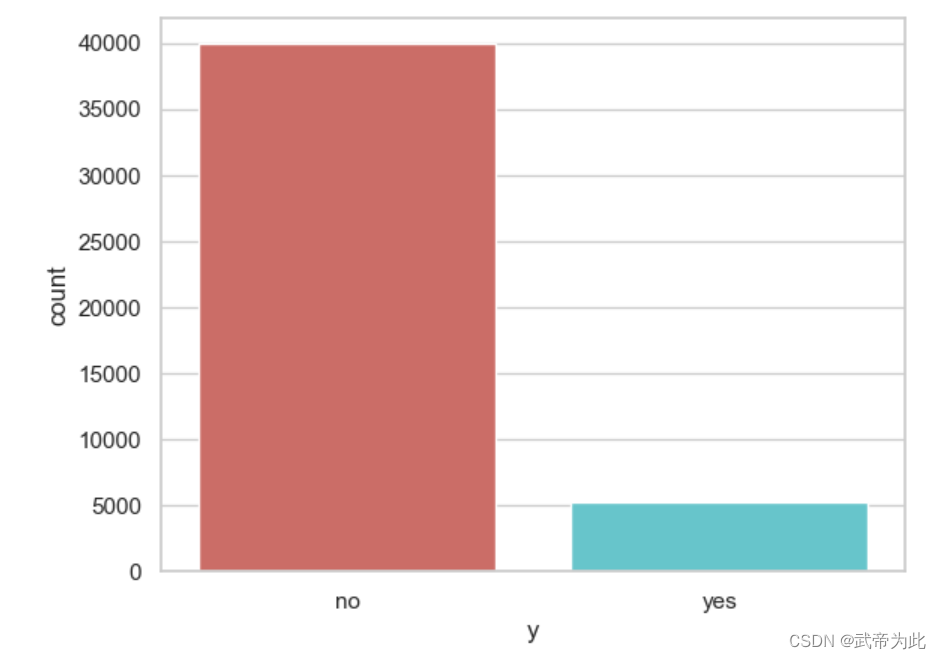
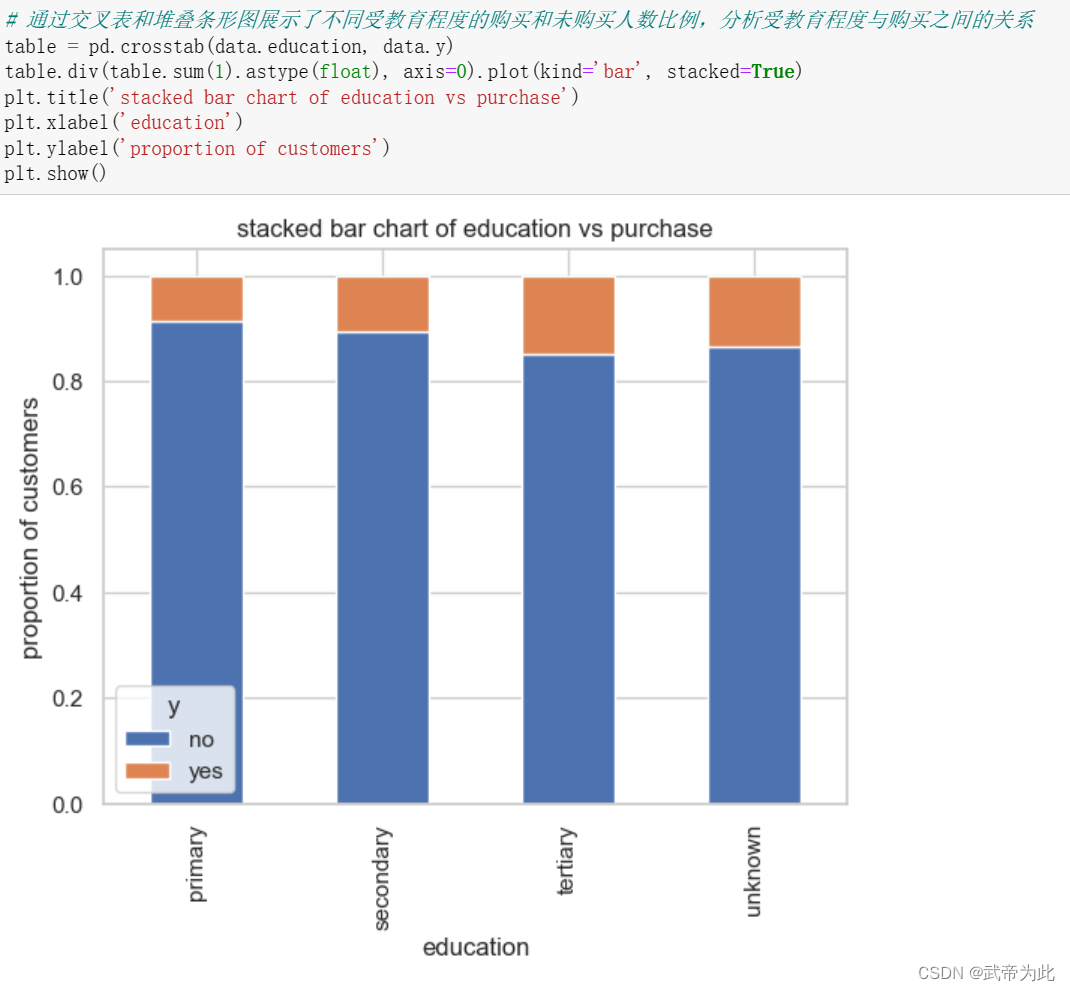
查询了目标变量 “y” 的值的分布，并通过柱状图进行可视化：

data['y'].value_counts()
print(data['y'].value_counts())

sns.countplot(x='y', data=data, palette='hls')
plt.show()

# 计算y值分布的百分比
count_no_sub = len(data[data['y'] == 'no'])
count_sub = len(data[data['y'] == 'yes'])
pct_of_no_sub = count_no_sub / (count_no_sub + count_sub)
print('未开户的百分比：%.2f%%' % (pct_of_no_sub * 100))
pct_of_sub = count_sub / (count_no_sub + count_sub)
print('开户的百分比：%.2f%%' % (pct_of_sub * 100))

通过计算y值分布得知，原始数据集的分布不均匀，需要对其进行处理

…
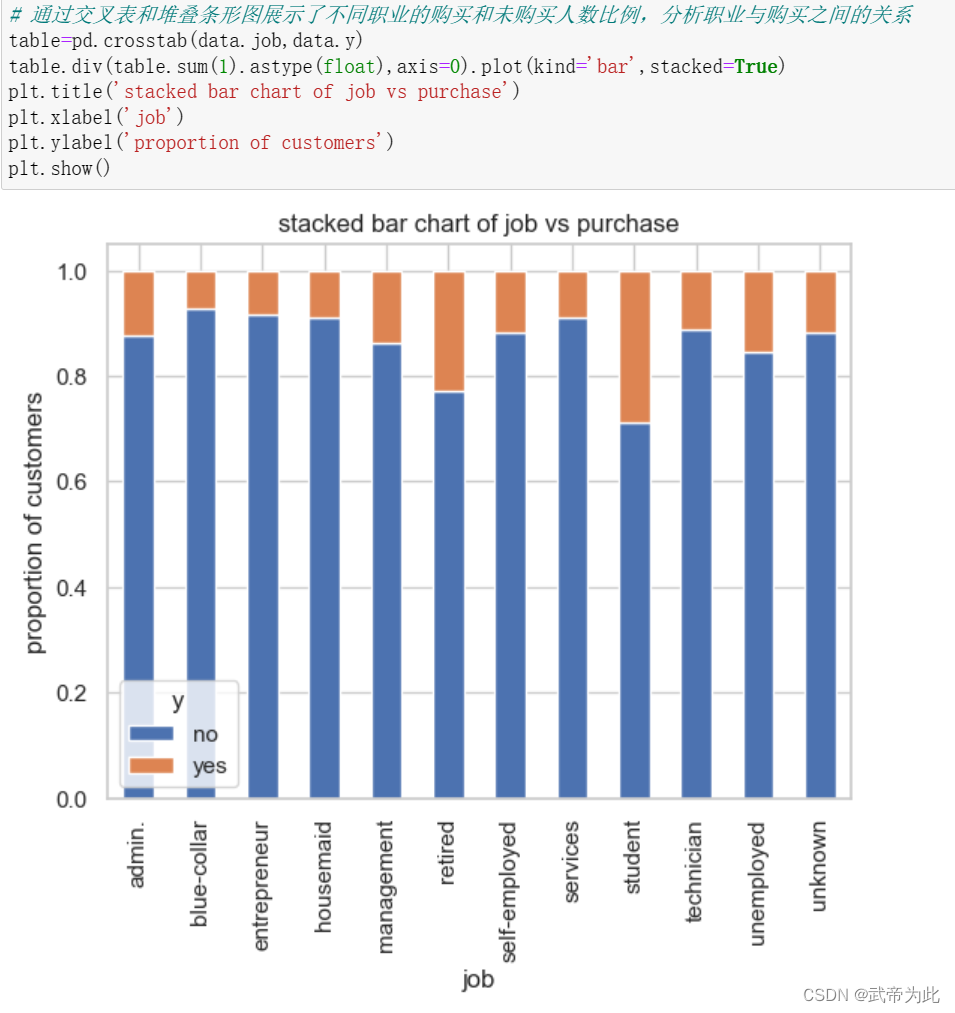
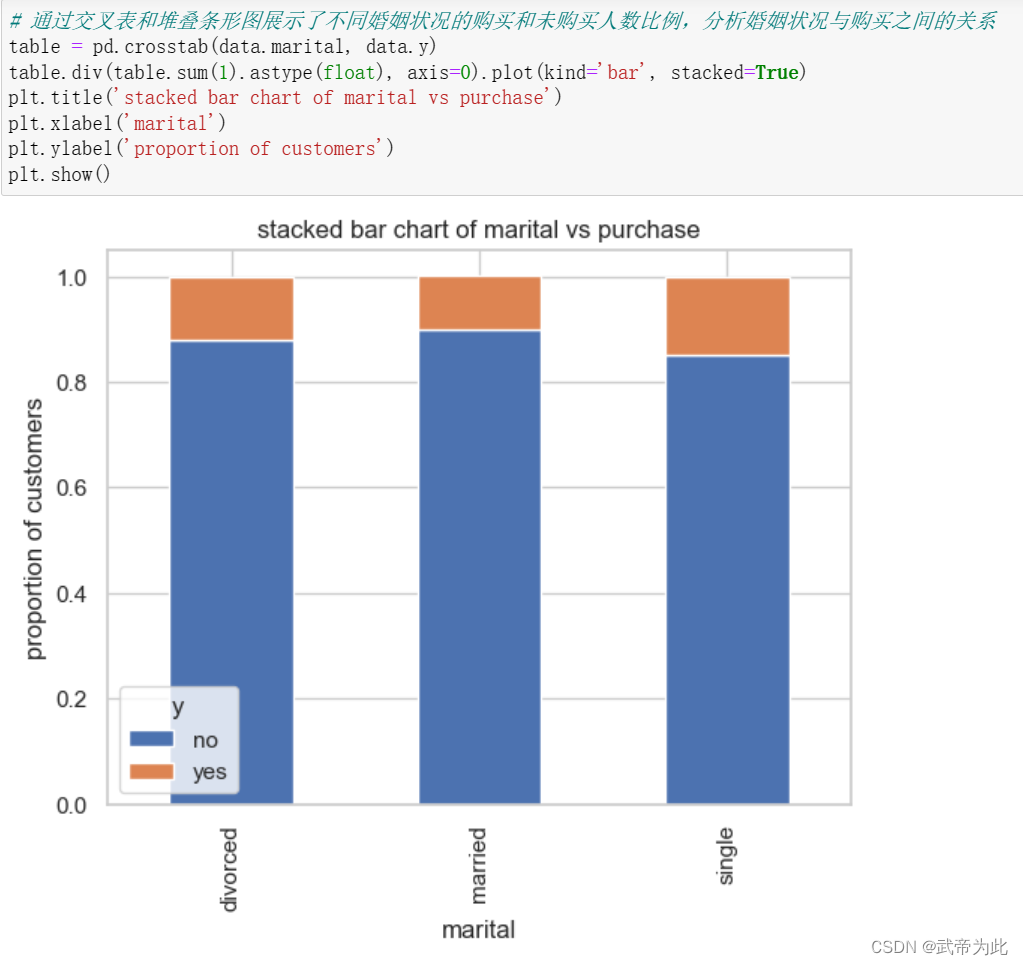
对不是数值型的数据进行独热编码

# 对分类变量（cat_vars）进行独热编码
cat_vars = ['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome']
for var in cat_vars:
    cat_list = pd.get_dummies(data[var], prefix=var)
    data = data.join(cat_list)
data_final = data.drop(cat_vars, axis=1)

print(data_final.columns.values)

由于之前发现原始数据集关于y值的分布并不均匀，所以需要对其处理，使用smote方法对数据进行过采样。

# 使用smote方法对数据进行过采样
from imblearn.over_sampling import SMOTE
X = data_final.loc[:, data_final.columns != 'y']
y = data_final.loc[:, data_final.columns == 'y'].values.ravel()

os = SMOTE(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

columns = X_train.columns
os_data_X, os_data_y = os.fit_resample(X_train, y_train)
os_data_X = pd.DataFrame(data=os_data_X, columns=columns)
os_data_y = pd.DataFrame(data=os_data_y, columns=['y'])

# 检查过采样后的数据
print('过采样后的数据个数：', len(os_data_X))
print('未开户的个数：', len(os_data_y[os_data_y['y'] == 'no']))
print('开户的个数：', len(os_data_y[os_data_y['y'] == 'yes']))
print('未开户的百分比：%.2f%%' % (len(os_data_y[os_data_y['y'] == 'no']) / len(os_data_X) * 100))
print('开户的百分比：%.2f%%' % (len(os_data_y[os_data_y['y'] == 'yes']) / len(os_data_X) * 100))

2.2 模型训练和评估

在完成了数据预处理之后，我们就可以开始训练我们的逻辑回归模型了。在这个过程中，我们会使用到 sklearn 库的 LogisticRegression 类。我们首先会将数据集划分为训练集和测试集，然后在训练集上训练模型，在测试集上评估模型的性能。

# 逻辑回归模型
from sklearn.linear_model import LogisticRegression
from sklearn import metrics

logreg = LogisticRegression()
logreg.fit(os_data_X, os_data_y.values.reshape(-1))

# 使用逻辑回归模型进行预测
y_pred = logreg.predict(X_test)
print('逻辑回归模型的准确率：', metrics.accuracy_score(y_test, y_pred))

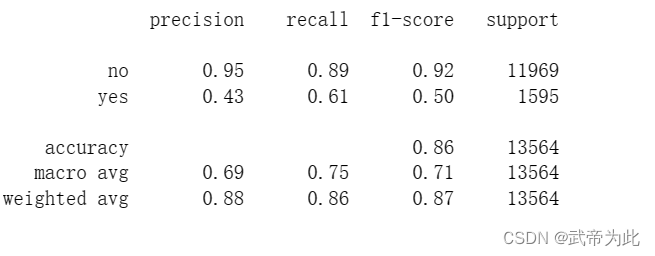
from sklearn.metrics import classification_report
print(classification_report(y_test, y_pred))

# 可视化混淆矩阵
from sklearn.metrics import confusion_matrix
confusion_matrix = confusion_matrix(y_test, y_pred)
print(confusion_matrix)

# 计算和绘制二分类模型的 ROC 曲线和计算 ROC AUC 分数
from sklearn.metrics import roc_auc_score, roc_curve
from sklearn.preprocessing import LabelEncoder

# 创建 LabelEncoder 实例
le = LabelEncoder()

# 将目标变量和预测结果编码为数值标签
y_test_encoded = le.fit_transform(y_test)
y_pred_encoded = le.transform(logreg.predict(X_test))

# 计算 ROC AUC 分数
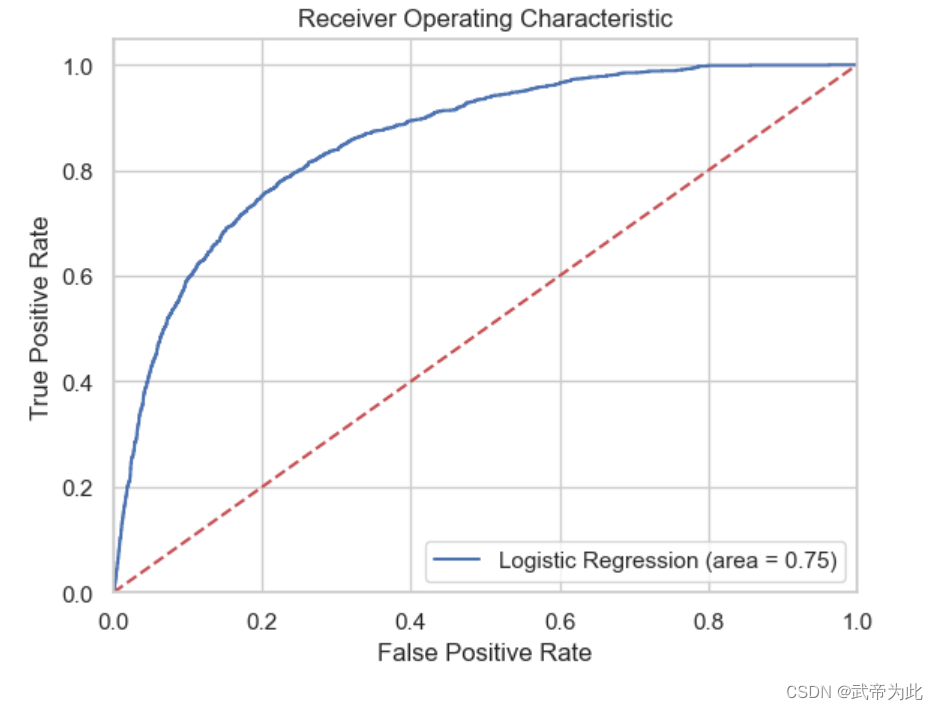
logit_roc_auc = roc_auc_score(y_test_encoded, y_pred_encoded)

# 计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_test_encoded, logreg.predict_proba(X_test)[:, 1])

# 绘制 ROC 曲线
plt.figure()
plt.plot(fpr, tpr, label='Logistic Regression (area = %0.2f)' % logit_roc_auc)
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()