前言

欢迎来到小K的Leetcode|代码随想录|专题化专栏，今天将为大家带来二分查找边界问题（循环不变量规则）的分享✨

---

核心

在开始今天的内容之前，我们首先要明确什么情况下可以使用二分——有序、无重复元素，当然也可以通过变形得到，再者就是边界条件的限定，while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？不要着急，我们通过下面的题目来揭开它的面目~

704. 二分查找

✨题目链接点这里
给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

✨第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right]

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[mid] > target) right 要赋值为 mid - 1，因为当前这个nums[mid]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+((right-left)>>2);
            if(nums[mid]==target) return mid;
            else if(nums[mid]>target) right=mid-1;
            else left=mid+1;
        }
        return -1;
    }
};

✨第二种写法，定义 target 是在一个在左闭右开的区间里，也就是[left, right)

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[mid] > target) right 更新为 mid，因为当前nums[mid]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为mid，即：下一个查询区间不会去比较nums[mid]

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left=0,right=nums.size();
        while(left<right)
        {
            int mid=left+((right-left)>>2);
            if(nums[mid]==target) return mid;
            else if(nums[mid]>target) right=mid;
            else left=mid+1;
        }
        return -1;
    }
};

---

367. 有效的完全平方数

✨题目链接点这里
给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。不能使用任何内置的库函数，如 sqrt 。
示例 1：

输入：num = 16
输出：true
解释：返回 true ，因为 4 * 4 = 16 且 4 是一个整数。

示例 2：

输入：num = 14
输出：false
解释：返回 false ，因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。

提示：

1 <= num <= 231 - 1

这个题目就是简单的二分应用

class Solution {
public:
    bool isPerfectSquare(int num)
    {
        int left=0,right=num;
        while(left<=right){
            int mid=left+((right-left)>>1);
            long square=(long)mid*mid;
            if(square==num) return true;
            else if(square<num) left=mid+1;
            else right=mid-1;
        }
        return false;
    }
};

---

69. x 的平方根

✨题目链接点这里
给你一个非负整数 x ，计算并返回 x 的 算术平方根 。由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示：

0 <= x <= 231 - 1

此题我还琢磨了好半天，最后发现思路很简单，由于这里是取整，所以所求的平方<=x，满足这种情况的我们记录一下（可能是答案），继续判断，看看有没有更贴切的，没有就返回记录的那种情况，剩下的情况用常规二分判断即可

class Solution {
public:
    int mySqrt(int x) 
    {
        int left=0,right=x,ans=-1;
        while(left<=right){
            int mid=left+((right-left)>>1);
            if((long long)mid*mid<=x){
                ans=mid;
                left=mid+1;
            }
            else right=mid-1;
        }
        return ans;
    }
};

---

35. 搜索插入位置

✨题目链接点这里
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

提示:

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为 无重复元素 的 升序 排列数组
-104 <= target <= 104

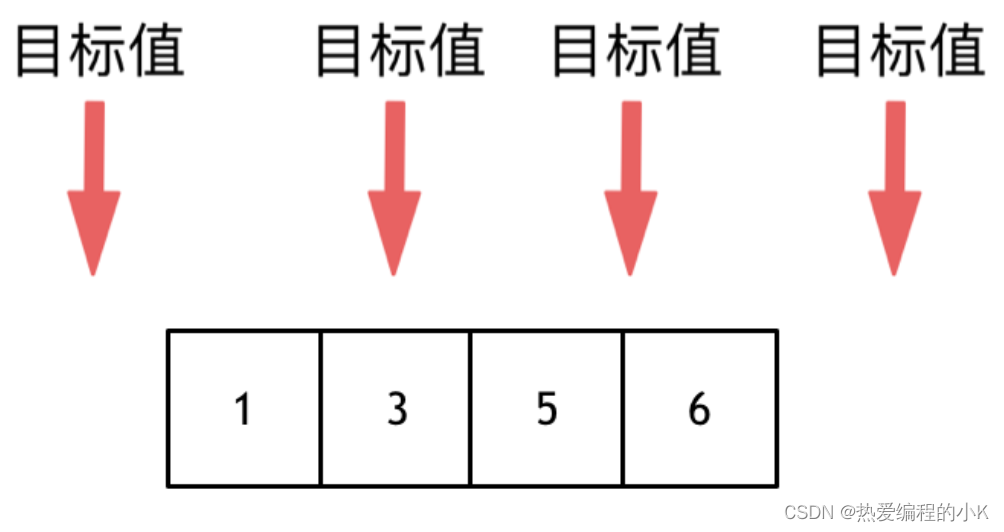
就下面的四总情况：

• 目标值在数组所有元素之前
• 目标值等于数组中某一个元素
• 目标值插入数组中的位置
• 目标值在数组所有元素之后

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) 
    {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+((right-left)>>1);
            if(nums[mid]==target) return mid;
            else if(nums[mid]>target) right=mid-1;
            else left=mid+1;
        }
        return right+1;
    }
};

---

34. 在排序数组中查找元素的第一个和最后一个位置

✨题目链接点这里
给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109

这题的关键就在于找上下边界，其实很简单，以第一个为例（左边界）就是在二分等于的基础上加判断条件当前中间元素等于目标值且不等于前面的一个元素或者当前中间元素等于目标值且为第一个元素，其他判断和二分一样

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        int left=getLeftIdx(nums,target), right=getRightIdx(nums,target);
        return {left,right};
    }
private:
    int getLeftIdx(vector<int>& nums, int target) 
    {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+((right-left)>>1);
            if(nums[mid]==target)
                if( mid==0 || nums[mid]!=nums[mid-1])
                    return mid;
                else right=mid-1;
            else if(nums[mid]>target) right=mid-1;
            else left=mid+1;
        }
        return -1;
    }
    int getRightIdx(vector<int>& nums, int target) 
    {
        int left=0,right=nums.size()-1;
        while(left<=right)
        {
            int mid=left+((right-left)>>1);
            if(nums[mid]==target)
                if( mid==nums.size()-1 || nums[mid]!=nums[mid+1])
                    return mid;
                else left=mid+1;
            else if(nums[mid]>target) right=mid-1;
            else left=mid+1;
        }
        return -1;
    }
};

---

总结

小K今天学习了二分查找的边界问题，以及几种场景下二分的切换，打卡第一天~加油！