作者:wuhanstudio
原文链接:https://zhuanlan.zhihu.com/p/611568999
最近在看无人驾驶的 Prediction 部分,可以利用 EKF (Extended Kalman Filter) 融合不同传感器的数据,例如 IMU, Lidar 和 GNSS,从而给出更加准确的状态预测。
刚好手边开发板有一个 6 轴的 IMU,本来打算试一下 卡尔曼滤波器 (Kalman Filter),然而 Kalman Filter 更适合 9 轴的传感器,也就是在 6 轴的基础上(3-axis Accel + 3-axis Gyro)融合 3 轴的磁力计。
对于一个只有 6 轴 IMU 的 MCU,轻量级的 互补滤波器 (Complementary Filter) 更加合适,利用 3 轴陀螺仪和 3 轴加速度计来估计开发板的姿态 (Pitch, Roll, Yaw)。
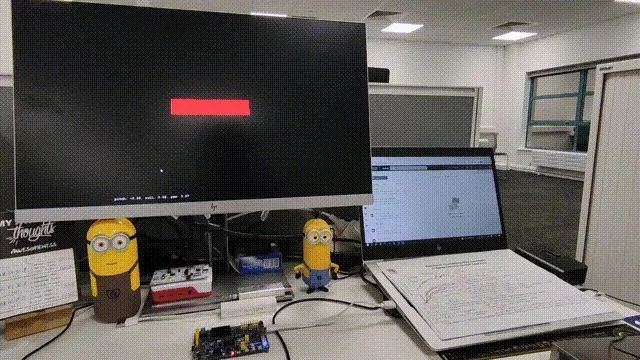
大致流程:首先用 RT-Thread 的 icm20608 软件包读取 陀螺仪 (Gyroscope) 和 加速度计 (Accelerometer) 的数据,分别计算出估计的角度,再用互补滤波器 (Complementary Filter) 融合两个角度估计、进行校正,其实核心算法的代码就 7 行。最后串口把数据发到电脑上,用 Python + OpenGL 可视化。
Github - STM32 IMU 互补滤波器 (RT-Thread):https://github.com/wuhanstudio/stm32-imu-filter
IMU 传感器 (Inertial Measurement Unit)
我们先介绍下从 I2C 总线读取出传感器原始数值后,如何处理得到加速度和旋转角速度。
一个六轴的 IMU 可以测量 x, y, z 三个方向的重力加速度,和绕三个轴的旋转角速度。比如,开发板如果静止放置在桌面上,会测量到 z 方向的重力加速度。
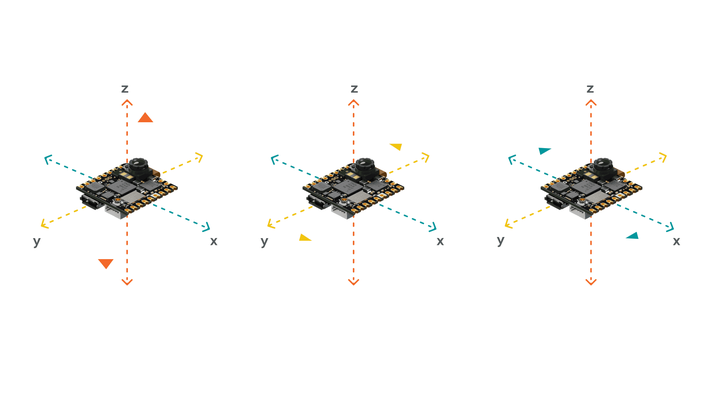
当然,如果开发板静止不动,绕三个轴的旋转速度都是 0。
由于传感器的输出实际上是来自 ADC 的 16 位数字信号,我们需要把它的单位转换成重力加速度 g。例如,我们可以选择测量范围
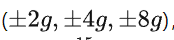
,默认是
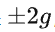
,也就是把传感器的 16 位输出
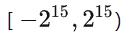
映射到 [-2g, 2g),于是
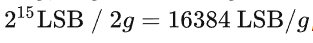
也就是下面 icm20608 芯片手册的 Sensitivity Scale Factor。
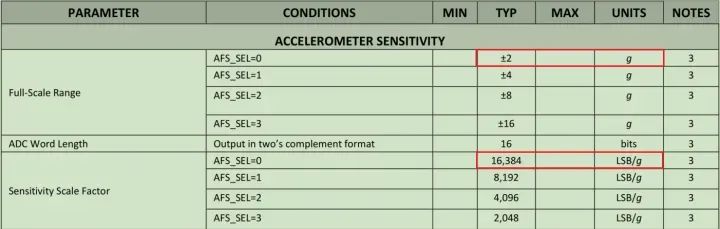
于是在代码里面,将原始的 int16 加速度数据除以 16384。
double aSensitivity = 16384;
accel_x = accel_x / aSensitivity;
accel_y = accel_y / aSensitivity;
accel_z = accel_z / aSensitivity;同样,我们可以换算出角速度
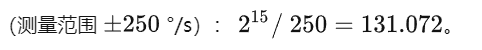
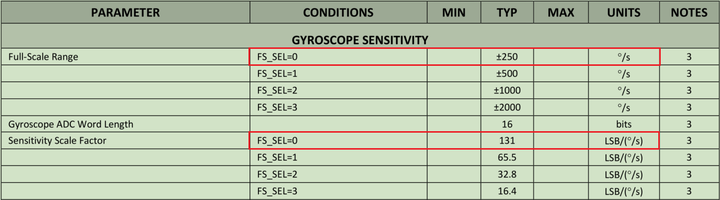
于是在代码里面,将原始的 int16 角速度数据除以 131。
double gSensitivity = 131;
gyrX = gyro_x / gSensitivity;
gyrY = gyro_y / gSensitivity;
gyrZ = gyro_z / gSensitivity;这样我们就把 ADC 输出的 int16 原始数据分布转换成了加速度单位 g,和旋转角速度单位 °/s.
互补滤波器 (Complementary Filter)
我们可以用 互补滤波器 结合 加速度 和 旋转速度 的测量值,得到更准确的姿态预测。
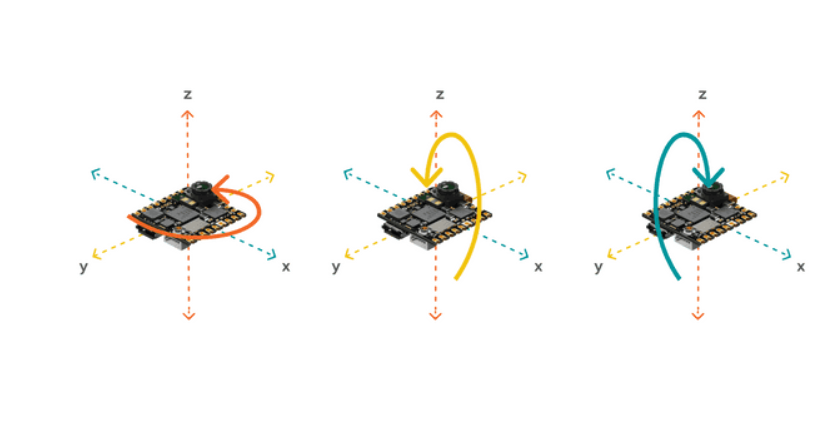
我们使用下面的图中的坐标系,绕 x 轴旋转的角度为 roll,绕 y 轴的旋转方向为 pitch,绕 z 轴旋转方向为 yaw。逆时针旋转为正,顺时针旋转为负。
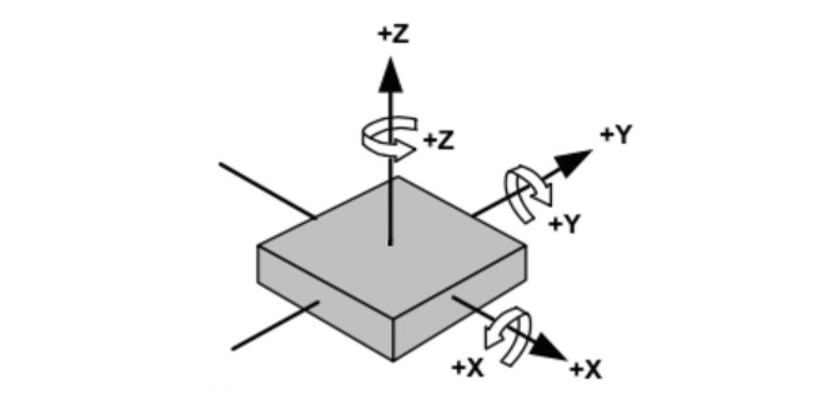
陀螺仪估计姿态
陀螺仪测量的是瞬间的旋转角速度,所以位置的估计其实就是时间的积分。例如,每过 100ms 测量一次旋转速度,旋转速度 x 时间 = 旋转角度。
// angles based on gyro (deg/s)
gx = gx + gyrX * TIME_STEP_MS / 1000;
gy = gy + gyrY * TIME_STEP_MS / 1000;
gz = gz + gyrZ * TIME_STEP_MS / 1000;当然,由于环境存在大量噪声,陀螺仪测量数据会存在随机的波动,这些噪声经过积分累积,最后会造成位置的漂移。
比如下面这张图,过了很长时间后,虽然开发板是静止的,但是右边的陀螺仪估计的位置,就无法回到原点,这就是长时间的累计误差造成的。
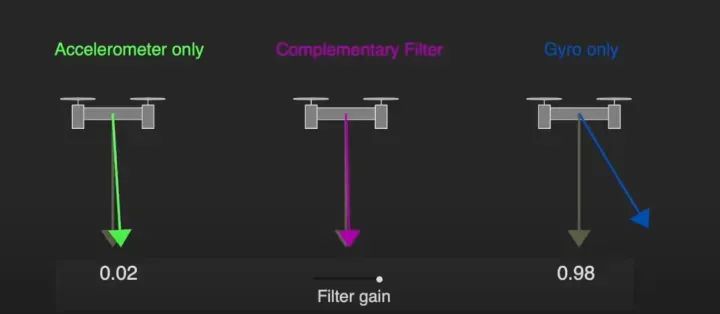
加速度计估计姿态
加速度计不需要积分,我们可以直接对当前加速度角度求 arctan 得到角度:
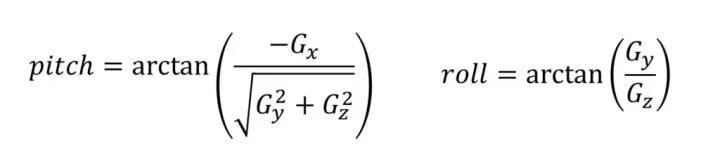
// angles based on accelerometer
ax = atan2(accelY, accelZ) * 180 / M_PI; // roll
ay = atan2(-accelX, sqrt( pow(accelY, 2) + pow(accelZ, 2))) * 180 / M_PI; // pitch不管我们的开发板绕 z 轴旋转多少度,重力加速度始终朝向地面。因此开发板静止状态,我们无法利用重力加速度知道 z 轴的旋转角度 (yaw),所以上面只计算 roll 和 pitch,最终 z 轴的旋转角度 yaw 会出现累计积分误差。
互补滤波器
我们需要结合2个测量值是因为:旋转速度短时间内比较准确,但是由于环境的噪声会产生一些随机运动,时间长了就会漂移,而加速度短时间内不一定准确,但是最终会维持稳定。
于是我们就可以取长补短,线性叠加2个测量值的估计,给出更准确的估计。
// complementary filter
gx = gx * 0.96 + ax * 0.04;
gy = gy * 0.96 + ay * 0.04;短时间内,我们相信陀螺仪测量的旋转角速度 (权值: 0.96);长时间内,环境噪声逐渐造成的漂移,由加速度计慢慢进行矫正 (权值: 0.04)。
总结
最后总结一下,其实核心代码一共就 7 行。我们先利用加速度求解姿态,再利用旋转角速度求解姿态,最后用互补滤波器进行一个线性叠加。
// angles based on gyro (deg/s)
gx = gx + gyrX * TIME_STEP_MS / 1000;
gy = gy + gyrY * TIME_STEP_MS / 1000;
gz = gz + gyrZ * TIME_STEP_MS / 1000;
// angles based on accelerometer
ax = atan2(accelY, accelZ) * 180 / M_PI; // roll
ay = atan2(-accelX, sqrt( pow(accelY, 2) + pow(accelZ, 2))) * 180 / M_PI; // pitch
// complementary filter
gx = gx * 0.96 + ax * 0.04;
gy = gy * 0.96 + ay * 0.04;References
https://github.com/mattzzw/Arduino-mpu6050
https://github.com/RT-Thread-pa

👇👇👇 点击阅读原文查看近期赛事