各位CSDN的uu们好呀,好久没有更新我的数据结构与算法专栏啦,今天,小雅兰继续来更新二叉树的内容,下面,让我们进入链式二叉树的世界吧!!!
二叉树链式结构的实现
二叉树链式结构的实现
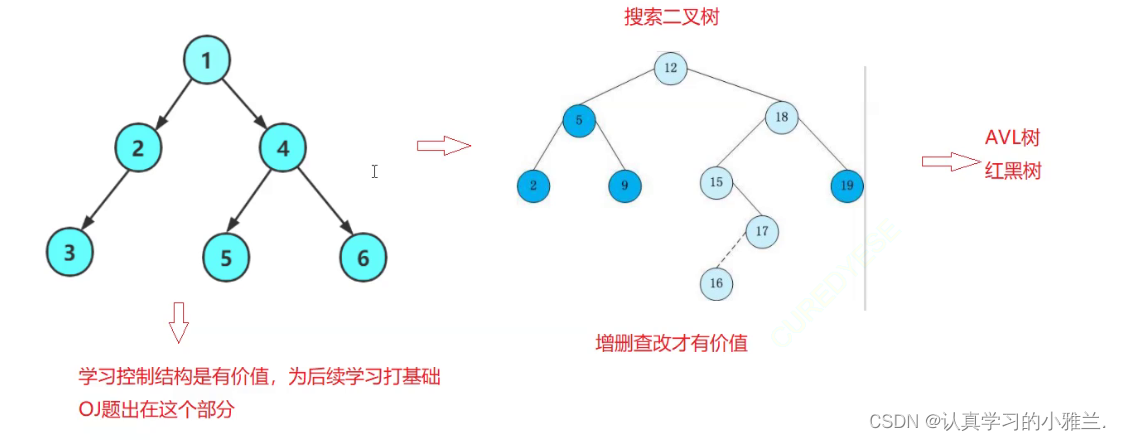
普通的二叉树的增删查改是没有价值的!!!
只有搜索二叉树的增删查改才有价值。
那么,为什么要学习普通二叉树,而不是一上来就学搜索二叉树呢?
因为,一上来就学习搜索二叉树实在是太难了!!!
而且,学习普通二叉树,主要是学习它的控制结构(递归),为后续学习打基础。
二叉树是:
1. 空树
2. 非空:根节点,根节点的左子树、根节点的右子树组成的。

从概念中可以看出,二叉树定义是递归式的。
二叉树的遍历
前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
按照规则,二叉树的遍历有:
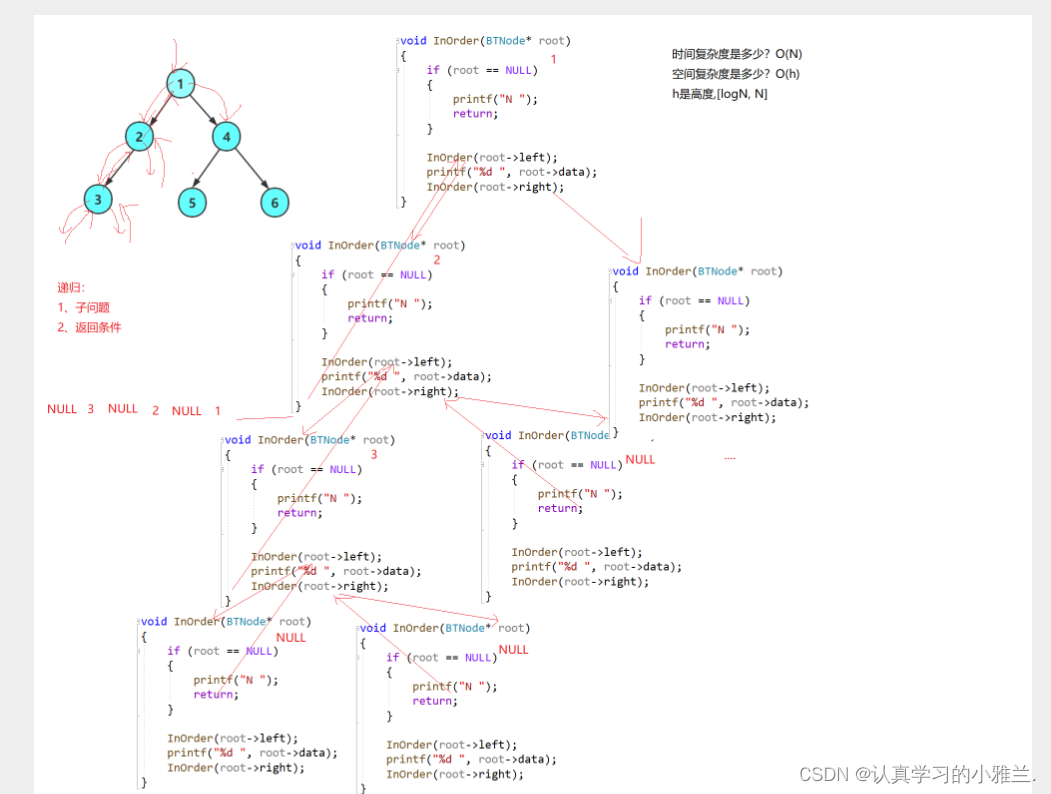
前序/中序/后序的递归结构遍历:
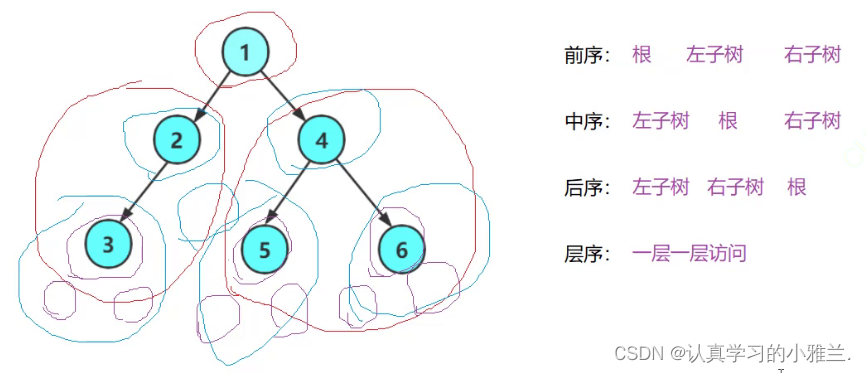
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
前序

1 2 3 4 5 6
中序

3 2 1 5 4 6
后序

3 2 5 6 4 1
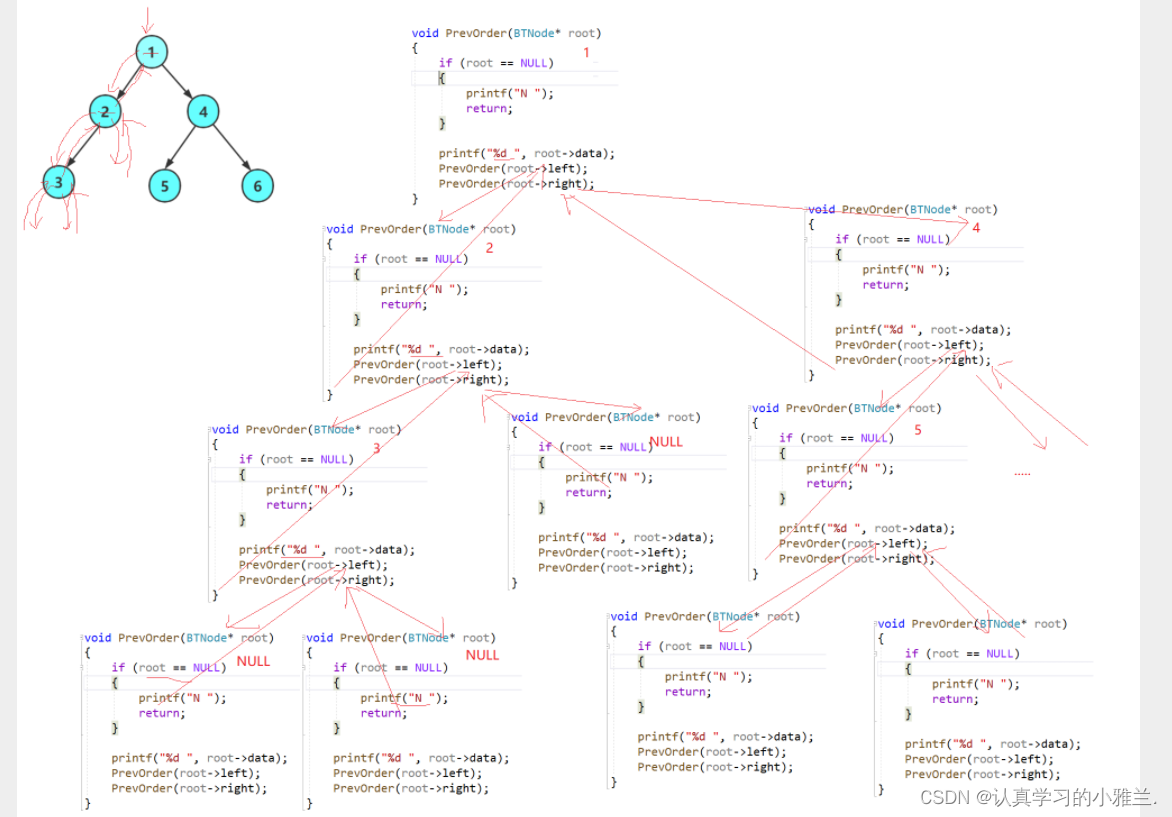
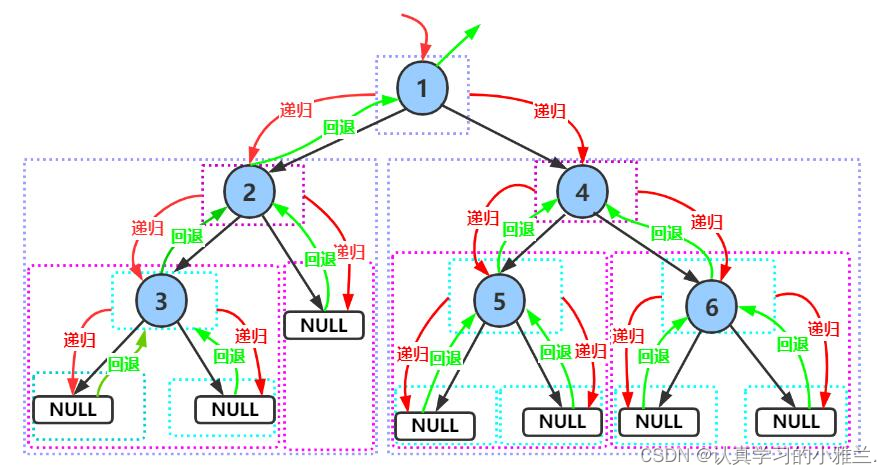
既然已经清楚了前序中序后序的物理过程,下面,就可以写代码啦!!!
前序
void PrevOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } printf("%d ", root->data); PrevOrder(root->left); PrevOrder(root->right); }

中序
void InOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } InOrder(root->left); printf("%d ", root->data); InOrder(root->right); }
后序
void PostOrder(BTNode* root) { if (root == NULL) { printf("NULL "); return; } PostOrder(root->left); PostOrder(root->right); printf("%d ", root->data); }


二叉树结点个数

不能这么写!!!
因为这是递归调用,不是循环,在循环里面就可以不断++size,就可以
但是这是在递归里面,在不同的栈帧里面,每个栈帧里面都有一个size,这样显然有问题
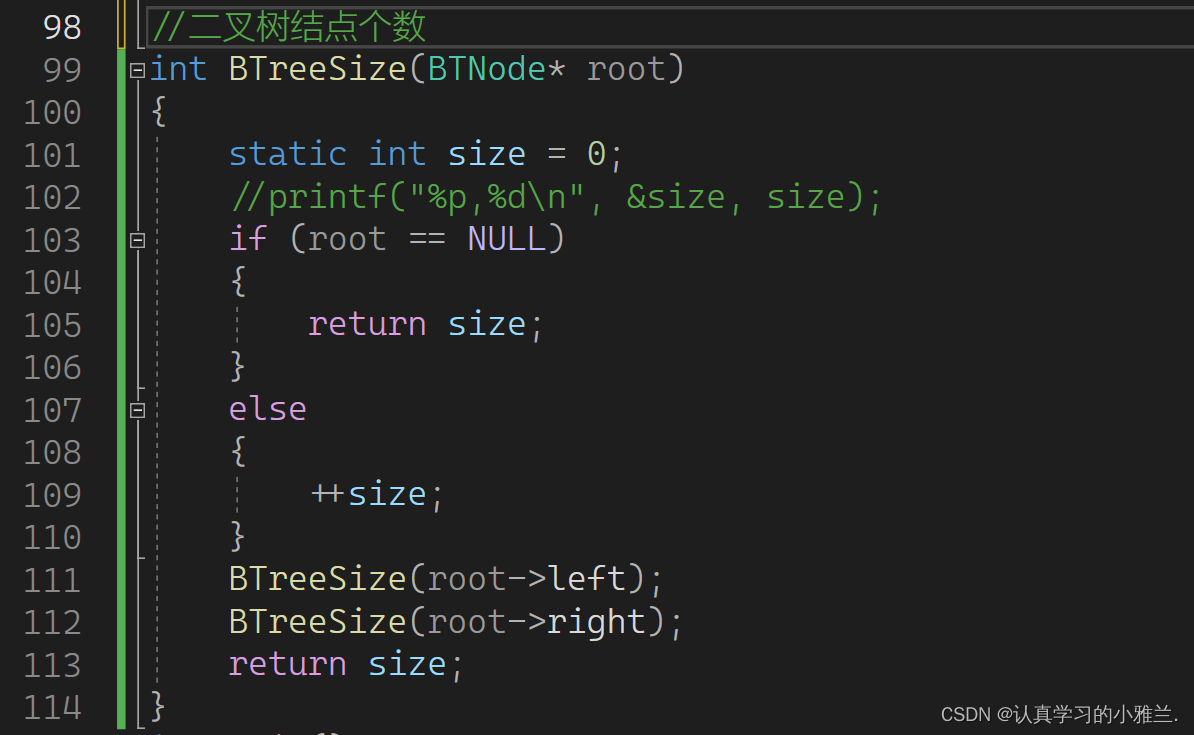
这样写也不行!!!
这个static定义的size就不在栈帧里面了,而是在静态区里面。
那么,该如何来验证这个问题呢?
//二叉树结点个数 void BTreeSize(BTNode* root) { static int size = 0; printf("%p\n", &size); if (root == NULL) { return; } else { ++size; } BTreeSize(root->left); BTreeSize(root->right); }
会发现:每次打印出的size的地址都一样!!!
//二叉树结点个数 void BTreeSize(BTNode* root) { static int size = 0; printf("%p,%d\n", &size,size); if (root == NULL) { return; } else { ++size; } BTreeSize(root->left); BTreeSize(root->right); }
会发现:并不是每次都把size置为0,size是发生变化的!!!
这样写表面上确确实实行得通,但是只要细细思索,会发现有大坑!!!
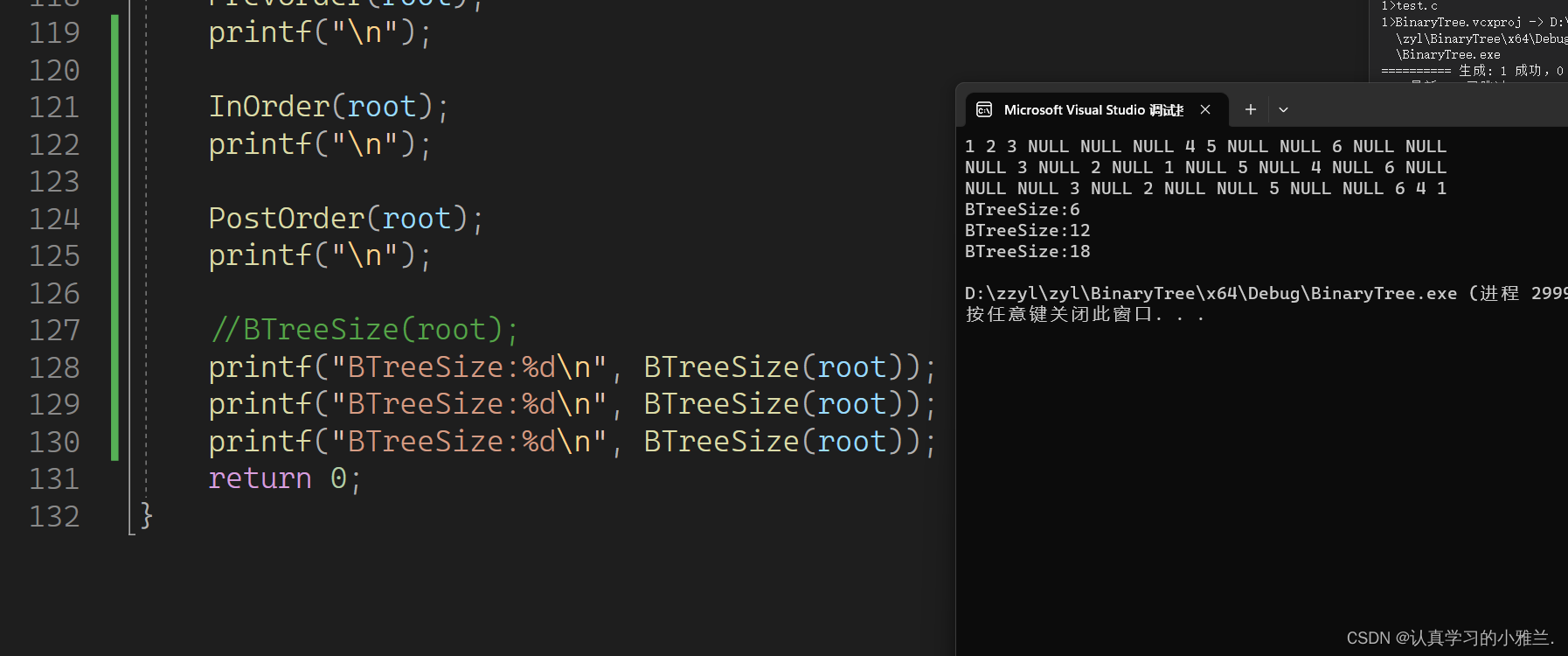
为什么结果会这样呢?
因为:size没办法置0!!!
那么,正确的写法该怎么写呢???
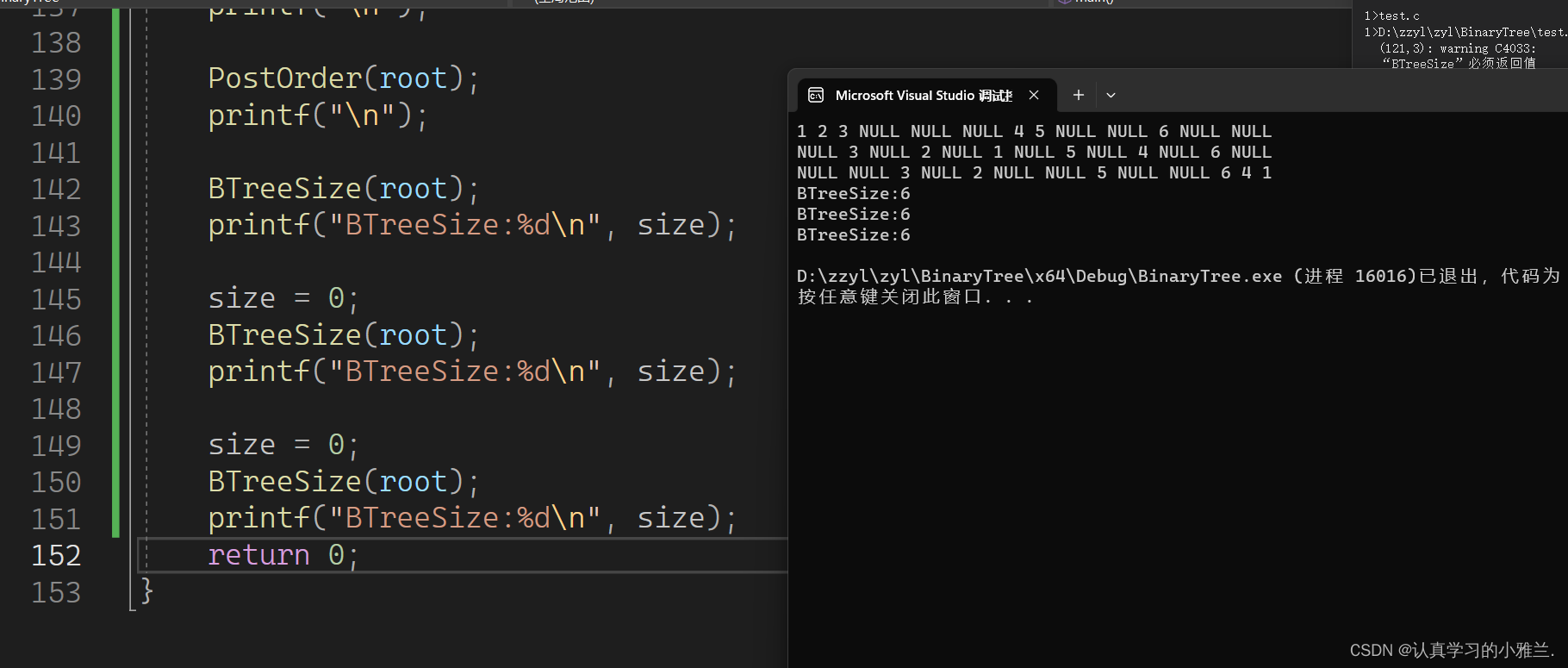
把size定义成全局变量!!!
//二叉树结点个数 int size = 0;//全局变量 void BTreeSize(BTNode* root) { if (root == NULL) { return; } else { ++size; } BTreeSize(root->left); BTreeSize(root->right); }int main() { BTreeSize(root); printf("BTreeSize:%d\n", size); size = 0; BTreeSize(root); printf("BTreeSize:%d\n", size); size = 0; BTreeSize(root); printf("BTreeSize:%d\n", size); return 0; }
这个方法是遍历记数法
求解这个问题还有另一种方法。

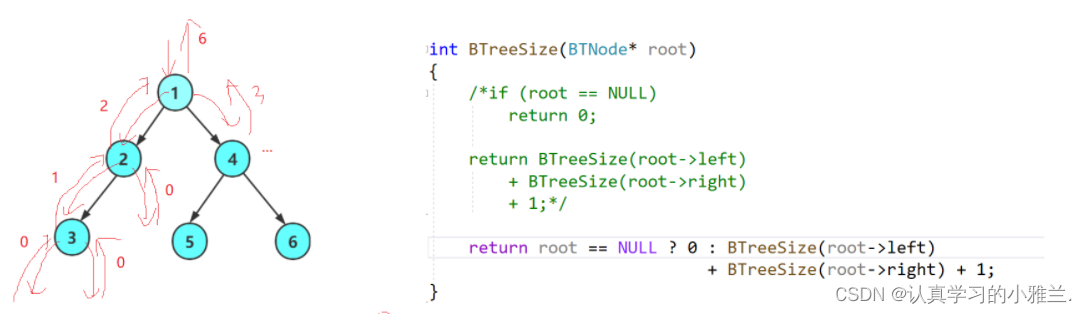
可以采用分治的方法!!!
//二叉树结点个数 int BTreeSize(BTNode* root) { if (root == NULL) { return 0; } else { return BTreeSize(root->left) + BTreeSize(root->right) + 1; } }另一种写法:
//二叉树结点个数 int BTreeSize(BTNode* root) { return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1; }

求叶子结点的个数
//求叶子结点的个数 int BTreeleafSize(BTNode* root) { if (root == NULL) { return 0; } if (root->left == NULL && root->right == NULL) { return 1; } return BTreeleafSize(root->left) + BTreeleafSize(root->right); }
目前整个的源代码:
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;BTNode* BuyNode(BTDataType x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
return NULL;
}
node->data = x;
node->left = NULL;
node->right = NULL;
return node;
}BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}//前序
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}//中序
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}//后序
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
二叉树结点个数
//int size = 0;//全局变量
//int BTreeSize(BTNode* root)
//{
// if (root == NULL)
// {
// return;
// }
// else
// {
// ++size;
// }
// BTreeSize(root->left);
// BTreeSize(root->right);
//}
二叉树结点个数
//int BTreeSize(BTNode* root)
//{
// if (root == NULL)
// {
// return 0;
// }
// else
// {
// return BTreeSize(root->left) + BTreeSize(root->right) + 1;
// }
//}
//二叉树结点个数
int BTreeSize(BTNode* root)
{
return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
//求叶子结点的个数
int BTreeleafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return BTreeleafSize(root->left) + BTreeleafSize(root->right);
}int main()
{
BTNode* root = CreatBinaryTree();
PrevOrder(root);
printf("\n");InOrder(root);
printf("\n");PostOrder(root);
printf("\n");/*BTreeSize(root);
printf("BTreeSize:%d\n", size);size = 0;
BTreeSize(root);
printf("BTreeSize:%d\n", size);size = 0;
BTreeSize(root);
printf("BTreeSize:%d\n", size);*/printf("BTreeSize:%d\n",BTreeSize(root));
return 0;
}
好啦,这只是二叉树的刚开始的部分知识点,接下来,小雅兰会继续更新数据结构与算法专栏啦,继续加油!!!