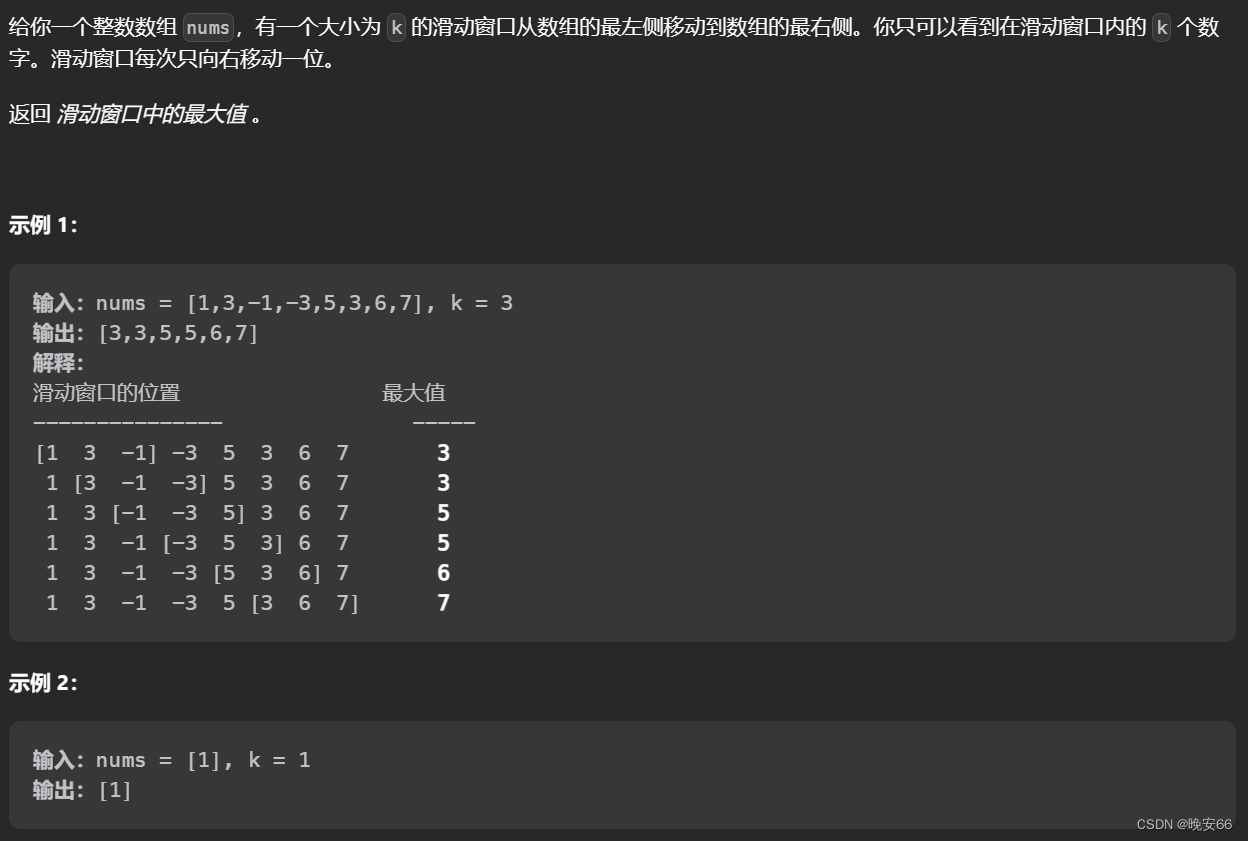
102. 二叉树的层序遍历

这里如果使用递归法会更好的理解,当我们储存每一层的答案数组的长度等于当前的level层数,说明我们这一层的节点都已经遍历完了,然后我们的下一次递归的level可以直接+1。
递归三要素:
递归终止条件:当node为None的时候,说明没有元素了,那么直接终止。
递归参数:level代表当前是第几层次,levels代表每一层的节点集合,node也就是咱们的节点。
单层循环逻辑: 当 当前节点的数量 = level层次的时候说明当前层次已经完成遍历。然后level +1进入下层循环。
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
levels = []
self.helper(root,0,levels)
return levels
def helper(self,node,level,levels):
if not node:
return []
if len(levels)==level:
levels.append([])
levels[level].append(node.val)
self.helper(node.left,level+1,levels)
self.helper(node.right,level+1,levels)226. 翻转二叉树
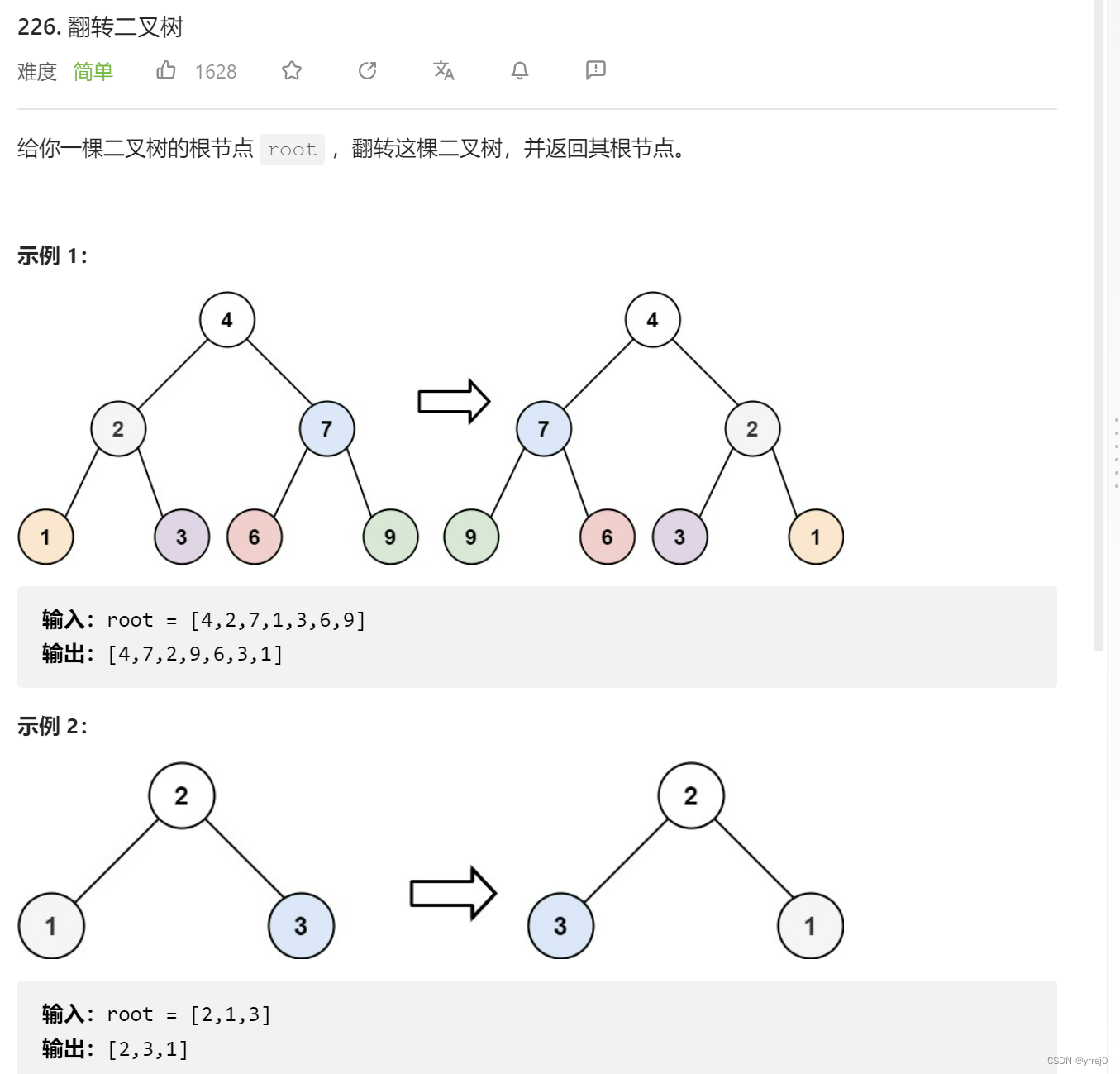
思路:这道题可以用前序或者后序遍历的方式来做,中间插入一个交换左右节点的过程就可以了。但是后序遍历不适用,因为后序遍历可能会导致左右节点交换多次。
递归三要素:
终止条件:当node为空的时候,return root
递归参数:root.left ,root.right
单层循环罗杰:当我们交换完左右节点之后,就按照正常的前序或者后序的顺序来做
代码:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
root.left,root.right = root.right,root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
101. 对称二叉树
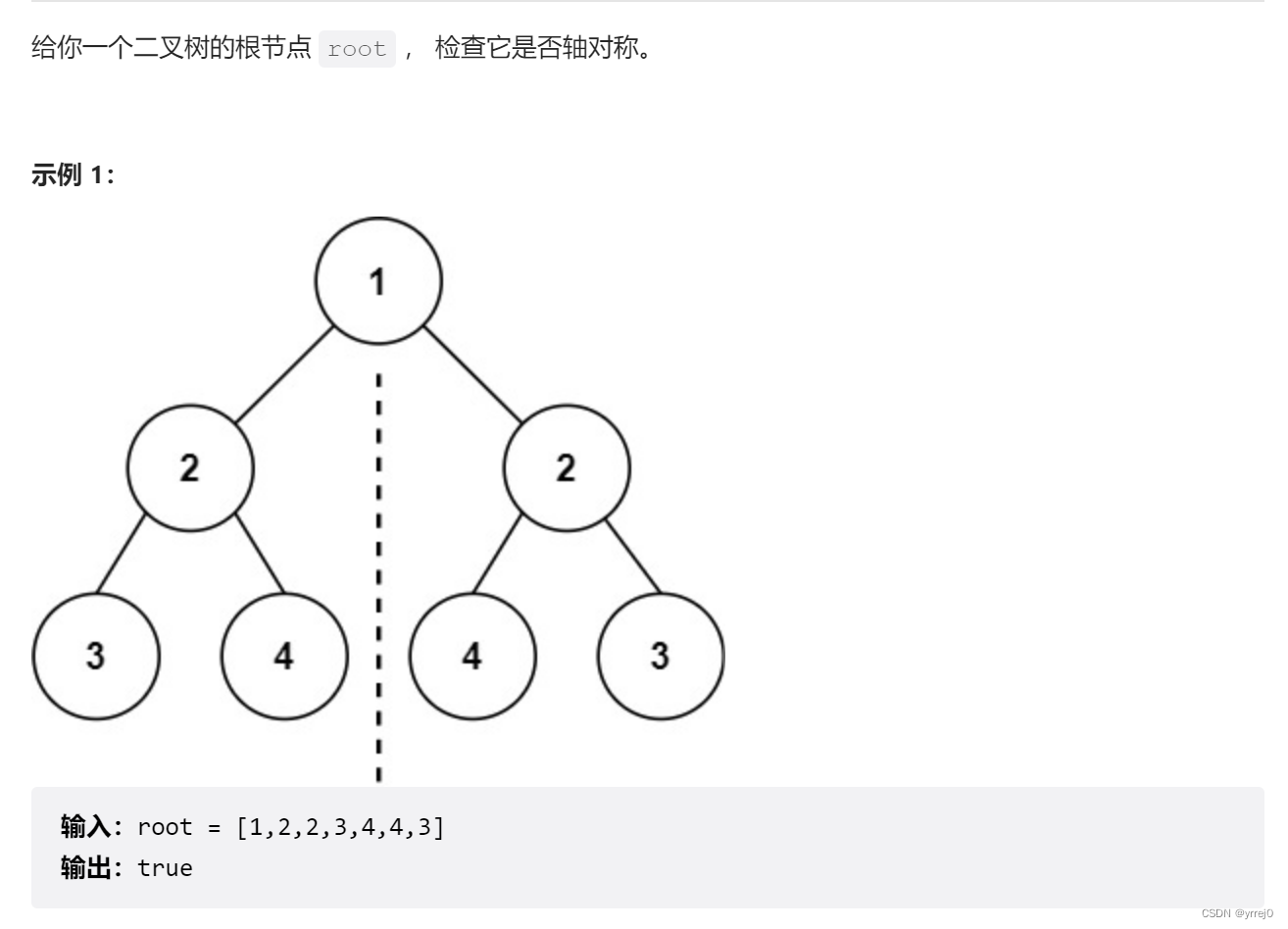
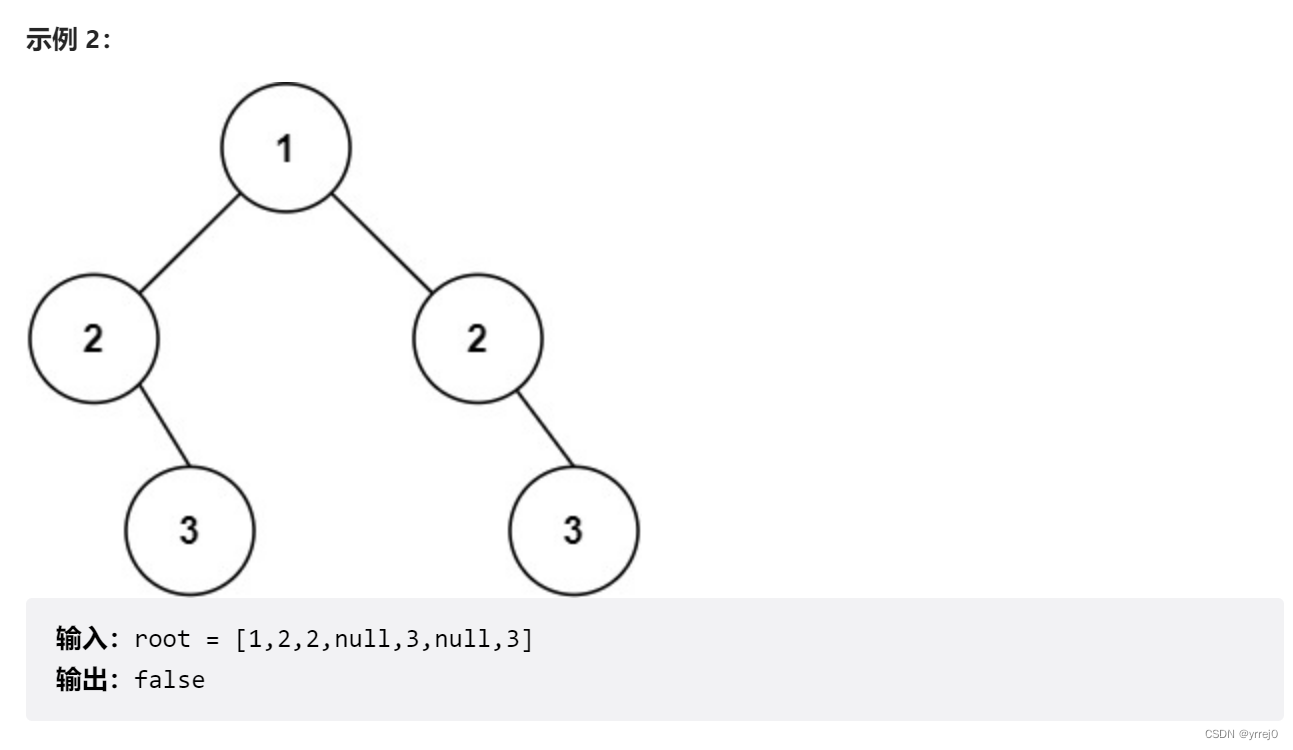
思路:
这里是实际上是判断两颗二叉树 能否反转,也就是说
左子树的左孩子应该对应右子树的右孩子
左子树的右孩子应该对应右子树的左孩子
在这之前有三种判断情况
当左右孩子都为空,return False
当左空右不空,return False
当左不空右空,return False
当左右都为空,return True
当左右都不为空,但是值不相等的时候,return False
当 root为空的时候,那就直接return True了,都不需要判断的
然后再去判断 我们最开始说的过程。
代码:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
return self.compare(root.left,root.right)
def compare(self,left,right):
if left==None and right!=None:
return False
elif right==None and left!=None:
return False
elif left==None and right==None:
return True
elif left.val!=right.val:
return False
else:
oustside = self.compare(left.left,right.right)
inside = self.compare(left.right,right.left)
return (inside and oustside)