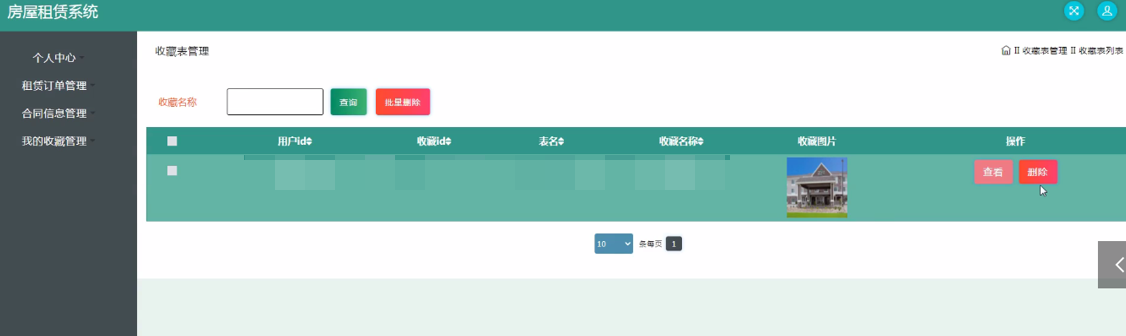
神经网络万能近似定理探索与实验

news2024/11/25 21:19:36

神经网络万能近似定理探索与实验

今天，我们来做神经网络万能近似定理的探索与实验。关于万能近似定理呢，就是说，对这个神经元的输出进行非线性激活函数处理，单层的神经网络就可以拟合任何一个函数。

下面先看我们搭建的第一个网络结构图：

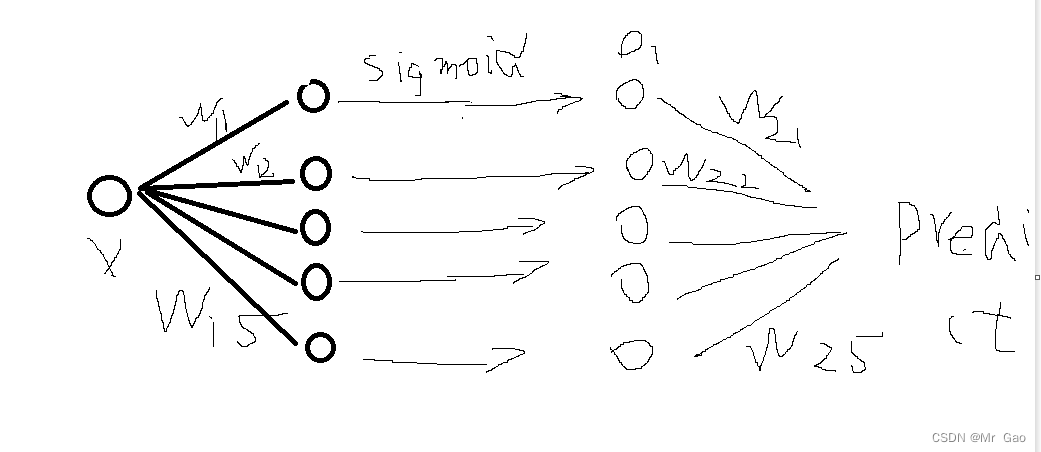
在这里插入图片描述
画的可能有点丑，就是搭建了一个隐藏层，使用sigmoid进行处理，最后加一个全连接层输出结果作为预测结果。

在实验中，我们使用的拟合函数是y=x+x^2+3

#coding=gbk

import torch
from torch.autograd import Variable
from torch.utils import data
import matplotlib.pyplot as plt

neuron_num=10
batch=32
sample_num=300
learn_rating=0.001
epoch=1000


x_data=torch.linspace(0,172,sample_num)
#print(x_data)

torch.manual_seed(10)

def function(x):
  return x*2+x**2+3
y_real=function(x_data)
#print(y_real)




def sampling(sample_num):
   
    #print(data_size)
    index_sequense=torch.randperm(sample_num)
    return index_sequense

w=torch.rand(neuron_num)
b=torch.randn(neuron_num)
w2=torch.randn(neuron_num)
b2=torch.randn(1)
def activation_function(x):
    return 1/(1+torch.sigmoid(-x))



def hidden_layer(w,b,x):
    return activation_function(w*x+b)

def  fully_connected_layer(w2,b2,x):
    return torch.dot(w2,x)+b2

def net(w,b,w2,b2,x):
    #print("w",w)
    #print("b",b)
    o1=hidden_layer(w,b,x)
    #print("o1",o1)
    #print("w2",w2)
    #print("b2",b2)
    o2=fully_connected_layer(w2,b2,o1)
 #   print("o2",o2)

    return o2

def get_grad(w,b,w2,b2,x,y_predict,y_real):
  

    o2=hidden_layer(w,b,x)

    l_of_w2=-(y_real-y_predict)*o2
    l_of_b2=-(y_real-y_predict)
    l_of_w=-(y_real-y_predict)*torch.dot(w2,o2*(1-o2))*x
    l_of_b=-(y_real-y_predict)*torch.dot(w2,o2*(1-o2))
    #print("grad")
    #print(l_of_w)
    #print(l_of_w2)
    #print(l_of_b)
    #print(l_of_b2)
    return l_of_w2,l_of_b2,l_of_w,l_of_b

def loss_function(y_predict,y_real):
    #print(y_predict,y_real)
    return torch.pow(y_predict-y_real,2)
loss_list=[]


def train():
    global w,w2,b,b2
    index=0
    for i in range(epoch):
        
        index_sequense=sampling(sample_num)
   
        W_g=torch.zeros(neuron_num)
        b_g=torch.zeros(neuron_num)
        W2_g=torch.zeros(neuron_num)
        b2_g=torch.zeros(1)
        loss=torch.tensor([0.0])
           
        for k in range(batch):
              try:
                   # print("x",x_data[index],index)
                   # print("w",w)
                        y_predict=net(w,b,w2,b2,x_data[index_sequense[index]])
                        #print("y_predict",y_predict)
                        #print("x:",x_data[index_sequense[index]])
                        #print("yreal:",y_real[index_sequense[index]])
                        get_grad(w,b,w2,b2,x_data[index_sequense[index]],y_predict,y_real[index_sequense[index]])
                      
                        l_of_w2,l_of_b2,l_of_w,l_of_b= get_grad(w,b,w2,b2,x_data[index_sequense[index]],y_predict,y_real[index_sequense[index]])
                        W_g=W_g+l_of_w
                        b_g=b_g+l_of_b
                        b2_g=b2_g+l_of_b2
                        W2_g=W2_g+l_of_w2
                        loss=loss+loss_function(y_predict,y_real[index_sequense[index]])
                        index=index+1
                       

              except:
                        index=0
                        index_sequense=sampling(sample_num)
        print("****************************loss is :",loss/batch)
        loss_list.append(loss/batch)
     
        W_g=W_g/batch
        b_g=b_g/batch
        b2_g=b2_g/batch
        W2_g=W2_g/batch
        w=w-learn_rating*W_g
        b=b-learn_rating*b_g
        w2=w2-learn_rating*W2_g
        b2=b2-learn_rating*b2_g
        #print(W2_g/batch)
        #print('w2',w2)
        #print(W_g/batch)
        #print('w1',w)


        


train()

y_predict=[]
for i in range(sample_num):

  y_predict.append(net(w,b,w2,b2,x_data[i]))

epoch_list=list(range(epoch))
plt.plot(epoch_list,loss_list,label='SGD')
plt.title("loss")
plt.legend()

plt.show()

plt.plot(x_data,y_real,label='real')
plt.plot(x_data,y_predict,label='predict')
plt.title(" Universal Theorem of Neural Networks")
plt.legend()
plt.show()
print(w,b,w2,b2)

跑出的实验结果如下：
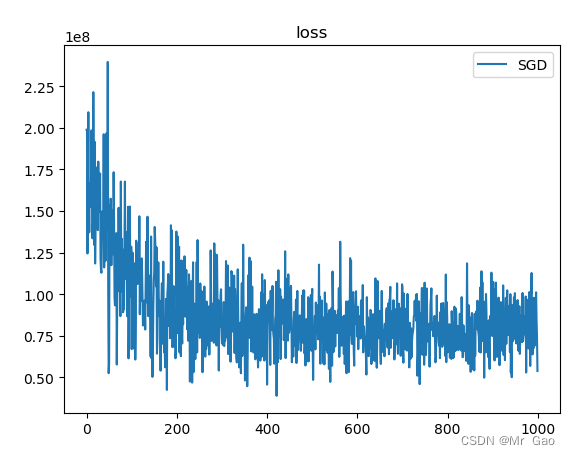
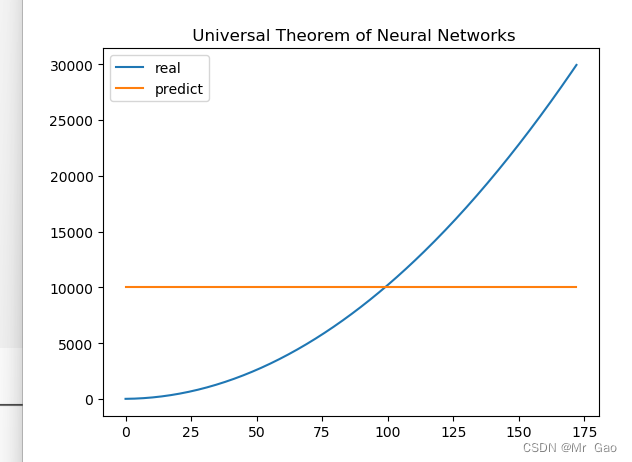
在这里插入图片描述
在这里插入图片描述

可以看到模型确实是由一定效果的，但是后面为什么跑出来的结果是一个直线呢，因为博主在推导的时候发现，w2i，i=1,2,的权重迭代时等量的，所以，才会出现这样的情况，因为神经元参数等量更新了，而且时同时更新，而且经过sigmoid转化，数值变为了1,才会发生这样的拟合情况。同时因为博主数据集真是的拟合值太大了，才会出现这样的问题
现在我们调整一下数据集
修改上述如下代码：

neuron_num=5
batch=32
sample_num=300
learn_rating=0.001
epoch=100


x_data=torch.linspace(0,3,sample_num)
#print(x_data)

torch.manual_seed(10)

def function(x):
  return x*2+x**2+3
y_real=function(x_data)
#print(y_real)





wz=torch.rand(neuron_num)
#print(wz)
w=torch.normal(0,10,size=(neuron_num,))
b=torch.normal(0,10,size=(neuron_num,))
w2=torch.normal(0,10,size=(neuron_num,))
b2=torch.normal(0,10,size=(1,))
#print(w,b)

会跑出下面一个结果：
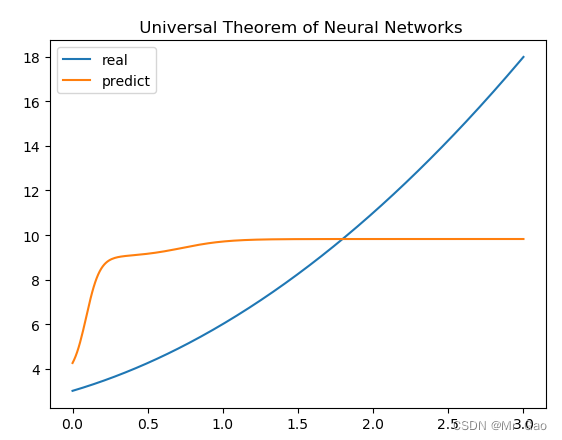
在这里插入图片描述
看起来是不是好了一点，现在我们增加训练轮次，来看一下：

neuron_num=5
batch=32
sample_num=300
learn_rating=0.001
epoch=1000

跑出的结果：
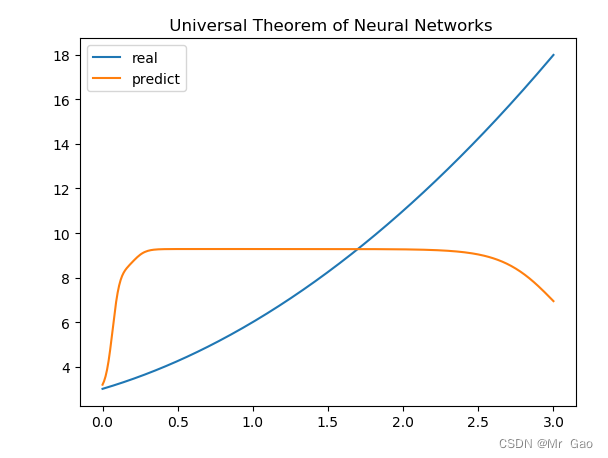
在这里插入图片描述
增加神经元数量：

neuron_num=10
batch=32
sample_num=300
learn_rating=0.001
epoch=1000

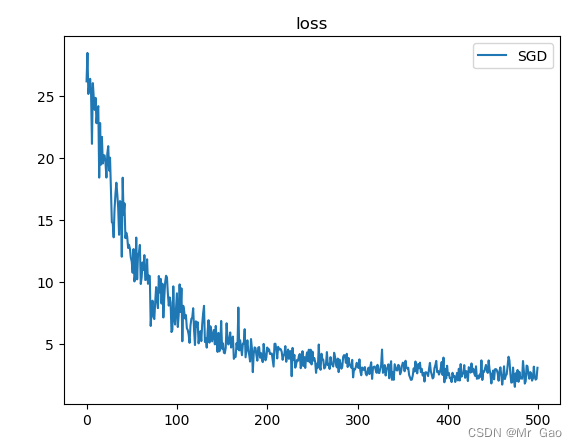
这个时候奇迹发生了：
loss结果：
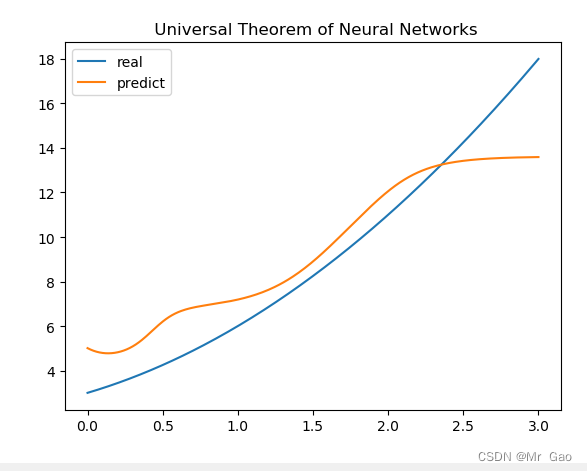
在这里插入图片描述
拟合结果
在这里插入图片描述

我们继续增加神经元个数，增加到20：

neuron_num=20
batch=32
sample_num=300
learn_rating=0.01
epoch=1000

其实博主后来发现了，学习率也很重要，也不是说神经元越多越好，学习率也是很重要的一方面。

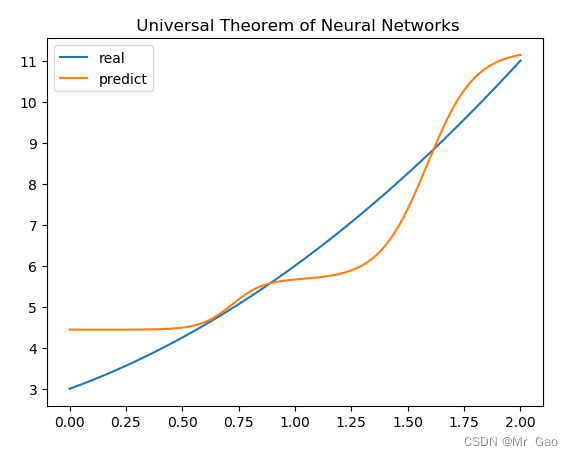
在这里插入图片描述
还有一百个神经元的：

neuron_num=100
batch=32
sample_num=300
learn_rating=0.01
epoch=1000

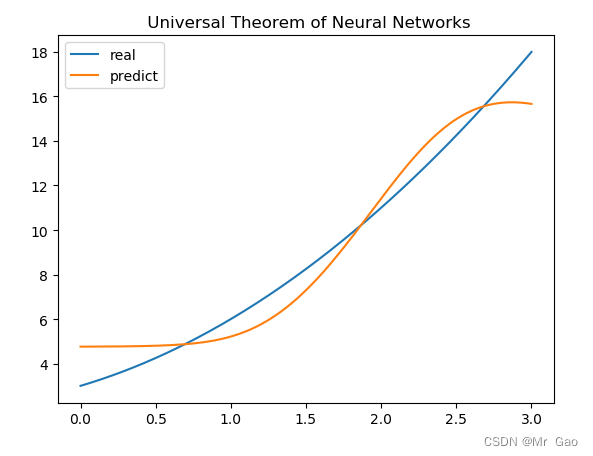
在这里插入图片描述
结果呢，可能还要好一点，sigmoid函数其实还好，还是很不错的，如果随着我们神经元的增多，确实效果会越来越好。
后面博主将函数改的更复杂了一些，跑出来结果也不错：

neuron_num=1000
batch=32
sample_num=300
learn_rating=0.001
epoch=3000


#print(x_data)


torch.manual_seed(10)

x_data=torch.linspace(0,3,sample_num)
def function(x):
  return x+x**3+3
y_real=function(x_data)
#print(y_real)

结果如下：
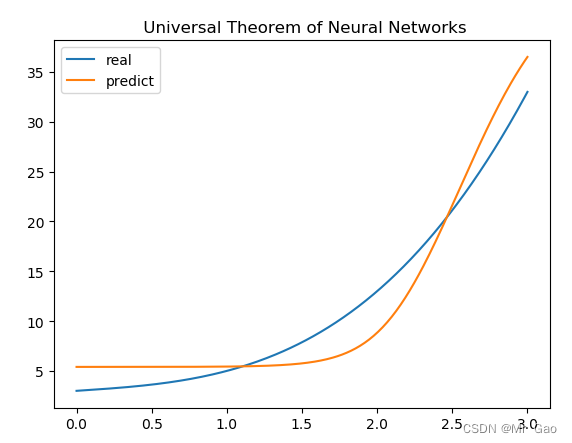
在这里插入图片描述
当然，越复杂的函数可能就需要越多的神经元，同时神经元初始化的数据也很重要，是否能很好的学习我们设定的函数并不是那么容易需要很多因素的功能作用，都需要我们去调整。

下面博主有做了relu激活函数的拟合代码，代码如下：

#coding=gbk

import torch
from torch.autograd import Variable
from torch.utils import data
import matplotlib.pyplot as plt

neuron_num=50

batch=32
sample_num=300
learn_rating=0.001
epoch=1000


#print(x_data)


torch.manual_seed(10)

x_data=torch.linspace(0,3,sample_num)
def function(x):
  return x+x**3+3
y_real=function(x_data)
#print(y_real)





wz=torch.rand(neuron_num)
#print(wz)
w=torch.normal(0,1,size=(neuron_num,))
b=torch.normal(0,1,size=(neuron_num,))
w2=torch.normal(0,1,size=(neuron_num,))
b2=torch.normal(0,1,size=(1,))
#print(w,b)


def sampling(sample_num):
   
    #print(data_size)
    index_sequense=torch.randperm(sample_num)
    return index_sequense
def activation_function(x):
    return 1/(1+torch.sigmoid(-x))


def activation_function2(x):
   
   # print(x.size())
    a=torch.rand(x.size())
    for i in range(x.size(0)):
        if x[i]<=0:
            a[i]=0.0
        else:
            a[i]=x[i]
    return a
    



def hidden_layer(w,b,x):
   # print("x:",x)
    return activation_function2(w*x+b)

def  fully_connected_layer(w2,b2,x):
    return torch.dot(w2,x)+b2

def net(w,b,w2,b2,x):
    #print("w",w)
    #print("b",b)
    o1=hidden_layer(w,b,x)
    #print("o1",o1)
    #print("w2",w2)
    #print("b2",b2)
    o2=fully_connected_layer(w2,b2,o1)
 #   print("o2",o2)

    return o2

def get_grad(w,b,w2,b2,x,y_predict,y_real):
  

    o2=hidden_layer(w,b,x)

    l_of_w2=-(y_real-y_predict)*o2
    l_of_b2=-(y_real-y_predict)

    a=torch.rand(o2.size())
    for i in range(o2.size(0)):
        if o2[i]<=0:
            a[i]=0.0
        else:
            a[i]=1
    l_of_w=-(y_real-y_predict)*torch.dot(w2,a)*x
    l_of_b=-(y_real-y_predict)*torch.dot(w2,a)
    #print("grad")
    #print(l_of_w)
    #print(l_of_w2)
    #print(l_of_b)
    #print(l_of_b2)
    return l_of_w2,l_of_b2,l_of_w,l_of_b

def loss_function(y_predict,y_real):
    #print(y_predict,y_real)
    return torch.pow(y_predict-y_real,2)
loss_list=[]


def train():
    global w,w2,b,b2
    index=0
    for i in range(epoch):
        
        index_sequense=sampling(sample_num)
   
        W_g=torch.zeros(neuron_num)
        b_g=torch.zeros(neuron_num)
        W2_g=torch.zeros(neuron_num)
        b2_g=torch.zeros(1)
        loss=torch.tensor([0.0])
           
        for k in range(batch):
              try:
                   # print("x",x_data[index],index)
                   # print("w",w)
                        y_predict=net(w,b,w2,b2,x_data[index_sequense[index]])
                        #print("y_predict",y_predict)
                        #print("x:",x_data[index_sequense[index]])
                        #print("yreal:",y_real[index_sequense[index]])
                        get_grad(w,b,w2,b2,x_data[index_sequense[index]],y_predict,y_real[index_sequense[index]])
                      
                        l_of_w2,l_of_b2,l_of_w,l_of_b= get_grad(w,b,w2,b2,x_data[index_sequense[index]],y_predict,y_real[index_sequense[index]])
                        W_g=W_g+l_of_w
                        b_g=b_g+l_of_b
                        b2_g=b2_g+l_of_b2
                        W2_g=W2_g+l_of_w2
                        loss=loss+loss_function(y_predict,y_real[index_sequense[index]])
                        index=index+1
                       

              except:
                        index=0
                        index_sequense=sampling(sample_num)
        print("****************************loss is :",loss/batch)
        loss_list.append(loss/batch)
     
        W_g=W_g/batch
        b_g=b_g/batch
        b2_g=b2_g/batch
        W2_g=W2_g/batch
        w=w-learn_rating*W_g
        b=b-learn_rating*b_g
        w2=w2-learn_rating*W2_g
        b2=b2-learn_rating*b2_g
        #print(W2_g/batch)
        #print('w2',w2)
        #print(W_g/batch)
        #print('w1',w)


        
#print(x_data.size())
y_predict=net(w,b,w2,b2,x_data[0])

train()

y_predict=[]
for i in range(sample_num):

  y_predict.append(net(w,b,w2,b2,x_data[i]))

epoch_list=list(range(epoch))
plt.plot(epoch_list,loss_list,label='SGD')
plt.title("loss")
plt.legend()

plt.show()

plt.plot(x_data,y_real,label='real')
plt.plot(x_data,y_predict,label='predict')
plt.title(" Universal Theorem of Neural Networks")
plt.legend()
plt.show()
print(w,b,w2,b2)

下面时拟合结果：
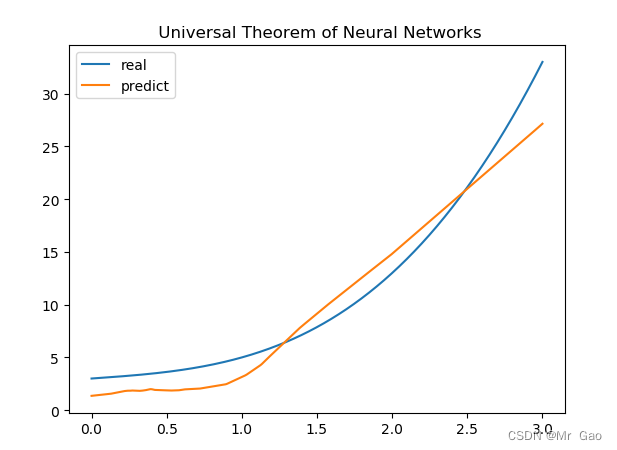
在这里插入图片描述
个人觉得relu函数的拟合性要比sigmoid函数强一点。好的，本次实验到此位置，感兴趣的同学可以多学习一下哈。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/746672.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

docker部署达梦数据库

docker部署达梦数据库

一、下载安装包 安装步骤&#xff1a; 先跟着网页走 注&#xff1a;第二步导入安装包&#xff0c;如果是在自己电脑上&#xff0c;就不一定要拷贝到/opt目录下&#xff0c;在安装包所在目录地址栏输入cmd&#xff0c;进入终端进行操作即可 操作到正常打印日志&#xff08;如…
阅读更多...
java项目之房屋租赁系统(ssm+mysql+jsp)

java项目之房屋租赁系统(ssm+mysql+jsp)

风定落花生&#xff0c;歌声逐流水&#xff0c;大家好我是风歌&#xff0c;混迹在java圈的辛苦码农。今天要和大家聊的是一款基于ssm的房屋租赁系统。技术交流和部署相关看文章末尾&#xff01; 开发环境&#xff1a; 后端&#xff1a; 开发语言&#xff1a;Java 框架&…
阅读更多...
尚硅谷Docker实战教程-笔记14【高级篇，Docker容器监控之CAdvisor+InfluxDB+Granfana、Docker终章总结】

尚硅谷Docker实战教程-笔记14【高级篇，Docker容器监控之CAdvisor+InfluxDB+Granfana、Docker终章总结】

尚硅谷大数据技术-教程-学习路线-笔记汇总表【课程资料下载】视频地址&#xff1a;尚硅谷Docker实战教程&#xff08;docker教程天花板&#xff09;_哔哩哔哩_bilibili 尚硅谷Docker实战教程-笔记01【基础篇&#xff0c;Docker理念简介、官网介绍、平台入门图解、平台架构图解】…
阅读更多...
centos7.9 连续登录失败处理

centos7.9 连续登录失败处理

如果有人恶意破解你的服务器&#xff0c;下面的操作可以起到一定的作用&#xff0c;连续登录失败锁定账户一段时间&#xff0c;让攻击者的成本增加&#xff0c;从而降低服务器被恶意破解的风险。 参考博客 https://blog.csdn.net/hjxloveqsx/article/details/129004832 https…
阅读更多...
MyBatis 中如何使用分页

MyBatis 中如何使用分页

MyBatis 中如何使用分页 在实际的项目开发中&#xff0c;我们经常需要对数据库中的数据进行分页查询&#xff0c;以提高数据查询的效率和用户体验。MyBatis 是一种流行的 Java 持久层框架&#xff0c;它提供了多种分页查询的方式&#xff0c;本文将介绍其中常用的两种方式&…
阅读更多...
MySQL数据库详解

MySQL数据库详解

文章目录 引言1. SQL1.1 SQL通用语法1.2 SQL分类1.3 DDL1.3.1 数据库操作1.3.2 表操作1.3.2.1 表操作-查询创建1.3.2.2 表操作-数据类型1.3.2.3 表操作-修改1.3.2.3 表操作-删除 1.4 DML1.4.1 添加数据1.4.2 修改数据1.4.3 删除数据 1.5 DQL1.5.1 基本语法1.5.2 基础查询1.5.3 …
阅读更多...
车载以太网之SOME/IP-SD专题篇

车载以太网之SOME/IP-SD专题篇

前言 首先，请问大家几个小小问题，你清楚： 你知道什么是SOME/IP SD吗？SOME/IP-SD报文是如何发送与接收的呢？SOME/IP-SD 存在哪几种Entry Type呢？SOME/IP-SD内部状态机转换又是如何？今天，我们就来一起探索并回答这些问题。为了便于大家理解，以下是本文的主题大纲： 目录…
阅读更多...
Sentinel 规则详解

Sentinel 规则详解

Sentinel 规则 流控规则 flow1、QPS流控2、并发线程数流控3、流控模式4、流控效果 熔断&#xff08;降级&#xff09;规则 degrade1、慢调用比例2、异常比例3、异常数 热点规则 param-flow授权规则 authority1、应用场景2、自定义来源3、授权规则配置 系统规则 前言&#xff1a…
阅读更多...
代码随想录day1 | 704.二分查找 27.移除元素

代码随想录day1 | 704.二分查找 27.移除元素

一、二分 1、二分易错点 1、循环变量 while(left < right) 还是while(left <right)2、判断条件 if(num[mid] > tar) mid right 还是 mid right -12、循环不变量 [left, right] [left, right) (left, right]3、左闭右闭写法 当时左闭右闭时&#xff0c;while循…
阅读更多...
从变分自动编码器到扩撒模型再到分数匹配模型的关系（VAE，Diffusion， score-based model）

从变分自动编码器到扩撒模型再到分数匹配模型的关系（VAE，Diffusion， score-based model）

https://arxiv.org/pdf/2208.11970.pdf
阅读更多...
2、基于kubeadm搭建K8S环境

2、基于kubeadm搭建K8S环境

目录 一、环境说明 二、初始化所有节点 三、修改三台服务器主机名&#xff0c;并写入host文件 四、调整内核参数 五、所有节点安装Docker 六、所有节点配置K8S源 七、所有节点安装kubeadm&#xff0c;kubelet和kubectl 八、部署 kubernetes Master 节点 九、k8s-node …
阅读更多...
基于docker的keepalived+MySQL主从实现MySQL高可用

基于docker的keepalived+MySQL主从实现MySQL高可用

因生产需要对MySQL做高可用&#xff0c;同时&#xff0c;资源有限&#xff0c;因此采用双节点主从keepalived方式实现高勇。另外因需要大批量部署MySQL集群&#xff0c;需要采用模板化部署&#xff0c;本方案采用将MySQL容器化&#xff0c;实现MySQL模板化配置部署。 部署环境及…
阅读更多...
SpringMVC学习笔记--上篇

SpringMVC学习笔记--上篇

SpringMVC学习笔记 1、SpringMVC 1.1、什么是SpringMVC Spring MVC是Spring Framework的一部分&#xff0c;是基于Java实现MVC的轻量级Web框架。 1.2、SpringMVC的特点 Spring MVC的特点&#xff1a; 轻量级&#xff0c;简单易学高效 , 基于请求响应的MVC框架与Spring兼容…
阅读更多...
Python深度学习-有向图合并、排序、最长路径计算

Python深度学习-有向图合并、排序、最长路径计算

一、有向图方向、权重表示方法 Python通常使用有向图中边的起点和终点来表示边的方向。例如&#xff0c;如果有一条从节点A到节点B的边&#xff0c;则可以使用以下方式表示该有向边&#xff1a; graph {A: {B: 1} }在这个例子中&#xff0c;节点A和节点B之间存在一条权重为1…
阅读更多...
谷歌插件下载Redux DevTools管理Redux数据

谷歌插件下载Redux DevTools管理Redux数据

我们在做 react-redux开发时 很多时候可能无法确定自己的数据有没有成功导进来 这里就有个不错的谷歌插件推荐给大家 大家可以下载我的资源 谷歌插件Redux DevTools 这里 我们打开 Google Chrome浏览器 然后 直接在谷歌浏览器上访问 chrome://extensions/ 如果你的第一次进入 …
阅读更多...
【网络安全】学过编程就是黑客？

【网络安全】学过编程就是黑客？

我们不可否认的是黑客为我们带来了巨大的财产损失于危机&#xff0c;即使其最初的思想是正确的。 个人主页&#xff1a;【&#x1f60a;许思王】 文章目录 前言黑客 &#x1f4bb;起源&#x1f697;发展&#x1f463;黑客守则&#xff08;真的假的&#x1f914;&#xff09;黑…
阅读更多...
合并cyclonedx格式的bom文件

合并cyclonedx格式的bom文件

1.工具下载 https://github.com/CycloneDX/cyclonedx-cli/releases 2.操作记录 Usage: cyclonedx [options] [command] Options: --version Show version information -?, -h, --help Show help and usage information Commands: add Add information to a BOM (currently…
阅读更多...
【图像处理】：相机对焦的原理和实现方法

【图像处理】：相机对焦的原理和实现方法

相机对焦的原理和实现方法 1 原理介绍&#xff1a;1.1点扩散函数“原理:1.2 测距原理:对焦的本质是测距&#xff1a;1.3.相位检测只原理: 2.实现方法2 1 原理介绍&#xff1a; 对焦有三种思路: 1.1点扩散函数“原理: 也就是观测画面中线条边缘的对比度&#xff0c;对比度最高…
阅读更多...
微信小程序代码审核，提示需要添加文娱-其他视频类目

微信小程序代码审核，提示需要添加文娱-其他视频类目

这个解决办法有三个 一个是按照指引去申请资质 第二个是通过后端写一个鉴权接口&#xff0c;审核时候去通过接口返回的布尔值去隐藏掉视频模块&#xff0c;通过后再显示出来 第三个是服务除视频内容外还存在其他形式的情况可以通过引入第三方视频插件来解决&#xff0c;但是…
阅读更多...
初识Golang，集简洁与性能与一体的语言

初识Golang，集简洁与性能与一体的语言

文章目录 一、Go语言介绍二、Go语言特性三、Go语言用途四、开发环境搭建五、建立工作区并创建Go程序六、入口文件基本代码介绍七、go命令介绍7.1 基本命令7.2 build 与 run命令7.3 install命令介绍 八、命名规范8.1 变量规范定义8.2 关键字8.3 保留字8.4 需要注意的问题 道阻且…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023