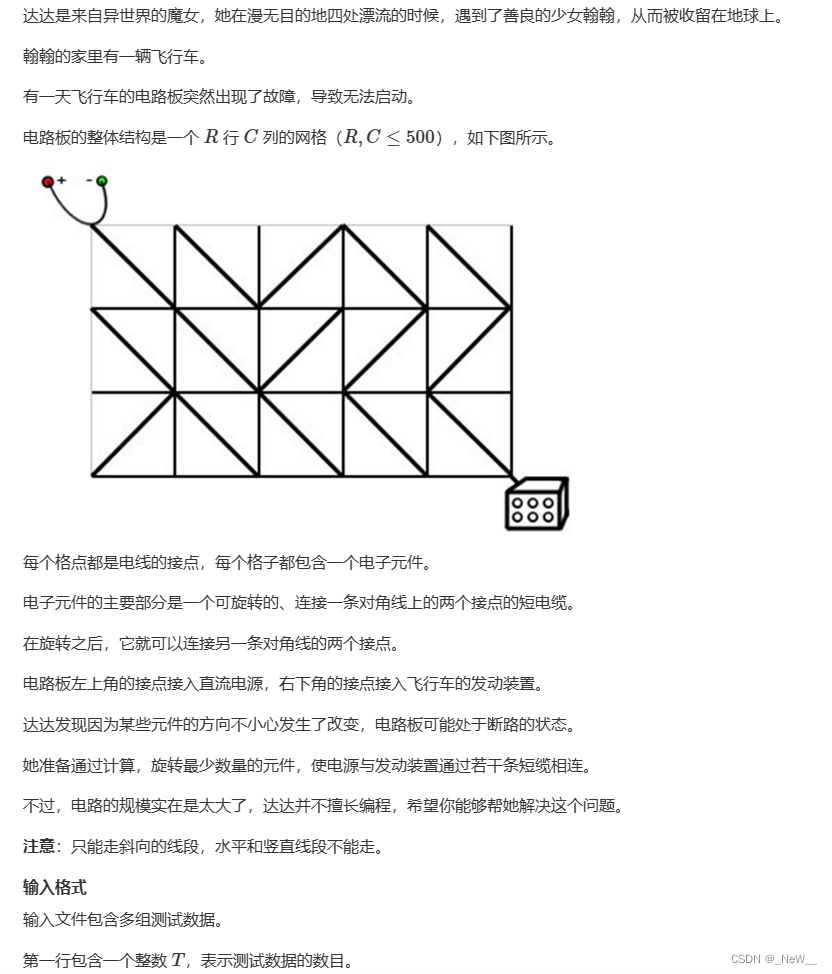
题意：从左上角走到右下角，且只能走斜线，斜线可以旋转，旋转斜线那么走过这条线，那么距离就加1，求最小的距离。

分析：有一个性质，因为起点是偶数点(0,0),那么它只能走到偶数点，奇数点一定走不到。

先在还要考虑怎么走

 

这道题为什么可以用双端队列可以做呢

因为dijstra+堆优化和这道题bfs+双端队列是一样的，双端队列每次边权为0的边加到头部，边权为1的边加到尾部，因为dijstra加对优化是正确的，那么bfs＋双端队列也是正确的，

#include<bits/stdc++.h>


using namespace std;

const int N = 510;

#define x first
#define y second
bool st[N][N];
char g[N][N];
int d[N][N];
int n,m;
typedef pair<int,int> PII;

int tx[4]={-1,-1,1,1},ty[4]={-1,1,1,-1};//点的偏移量
int ix[4]={-1,-1,0,0},iy[4]={-1,0,0,-1};//格子的偏移量

int bfs()
{
    memset(d,0x3f,sizeof d);
    memset(st,false,sizeof st);
    
    deque<PII> q;
    q.push_back({0,0});
    // st[0][0]=true;
    d[0][0]=0;
    char cs[]="\\/\\/";
    while(q.size())
    {
        auto t=q.front();
        q.pop_front();
        
        if(st[t.x][t.y]) continue;
        st[t.x][t.y]=true;//标记走过的点
        // cout<<t.x<<" "<<t.y<<endl;
        for(int i=0;i<4;i++)
        {
          int a=t.x+tx[i],b=t.y+ty[i];
          
          if(a<0||a>n||b<0||b>m) continue;
          
          int ca=t.x+ix[i],cb=t.y+iy[i];
          int dist=d[t.x][t.y]+(g[ca][cb]!=cs[i]);//判断需要不需要旋转边
          
          if(dist<d[a][b])//更新
          {
              d[a][b]=dist;
              if(g[ca][cb]!=cs[i]) q.push_back({a,b});
              else q.push_front({a,b});
          }
        }
    }
    return d[n][m];
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        for(int i=0;i<n;i++) scanf("%s",g[i]);
        
        int t=bfs();
        
        if(t==0x3f3f3f3f) cout<<"NO SOLUTION"<<endl;
        else cout<<d[n][m]<<endl;
    }
    
    return 0;
}