在上篇文章中,我们介绍了渲染流水线中的 DOM 生成、样式计算和布局三个阶段,那今天我们接着讲解渲染流水线后面的阶段。
这里还是先简单回顾下上节前三个阶段的主要内容:在 HTML 页面内容被提交给渲染引擎之后,渲染引擎首先将 HTML 解析为浏览器可以理解的 DOM;然后根据 CSS 样式表,计算出 DOM 树所有节点的样式;接着又计算每个元素的几何坐标位置,并将这些信息保存在布局树中。
分层
现在我们有了布局树,而且每个元素的具体位置信息都计算出来了,那么接下来是不是就要开始着手绘制页面了?
答案依然是否定的。
因为页面中有很多复杂的效果,如一些复杂的 3D 变换、页面滚动,或者使用 z-indexing 做 z 轴排序等,为了更加方便地实现这些效果,渲染引擎还需要为特定的节点生成专用的图层,并生成一棵对应的图层树(LayerTree)。如果你熟悉 PS,相信你会很容易理解图层的概念,正是这些图层叠加在一起构成了最终的页面图像。
要想直观地理解什么是图层,你可以打开 Chrome 的“开发者工具”,选择“Layers”标签,就可以可视化页面的分层情况,如下图所示:
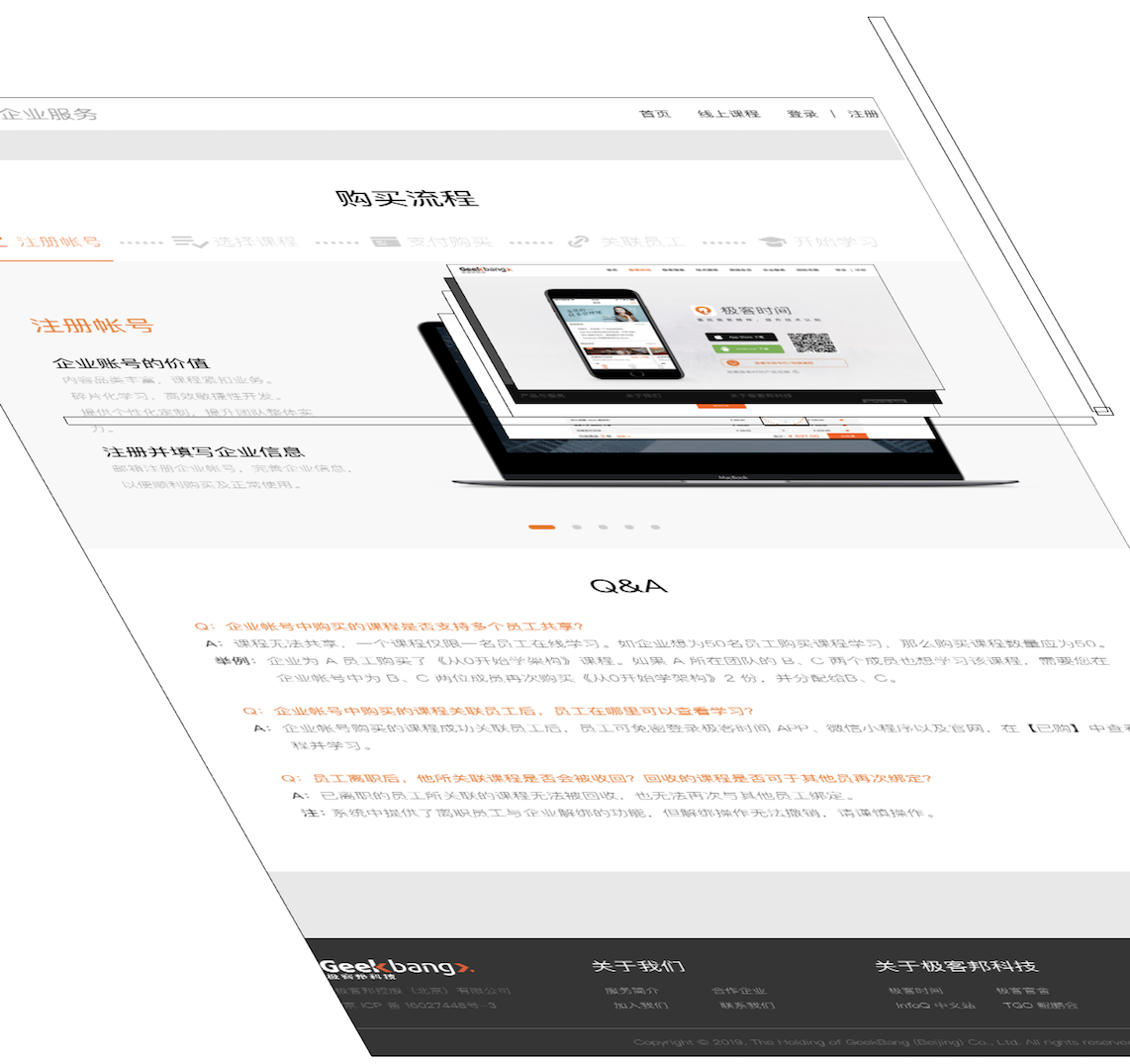
从上图可以看出,渲染引擎给页面分了很多图层,这些图层按照一定顺序叠加在一起,就形成了最终的页面,你可以参考下图:

![关于SpringBoot、Nginx 请求参数包含 [] 特殊符号 返回400状态](https://img-blog.csdnimg.cn/7efd894b6f054017a7d2c48b475f4d51.png)