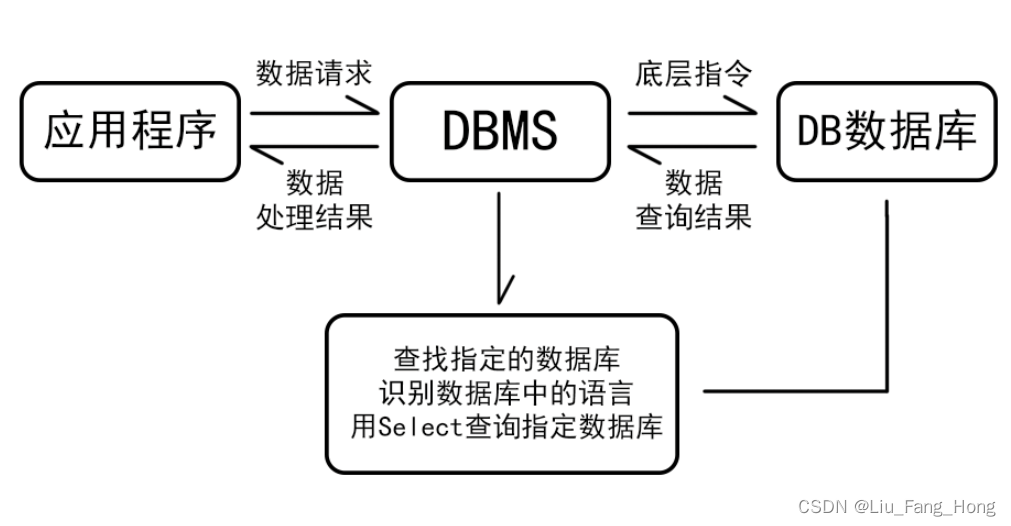
泊松比(Poisson’s ratio)提供了有关不同材料在负载下如何变形的关键信息,将施加载荷的方向称为纵向(longitudinal direction),将垂直方向称为横向(lateral directions)
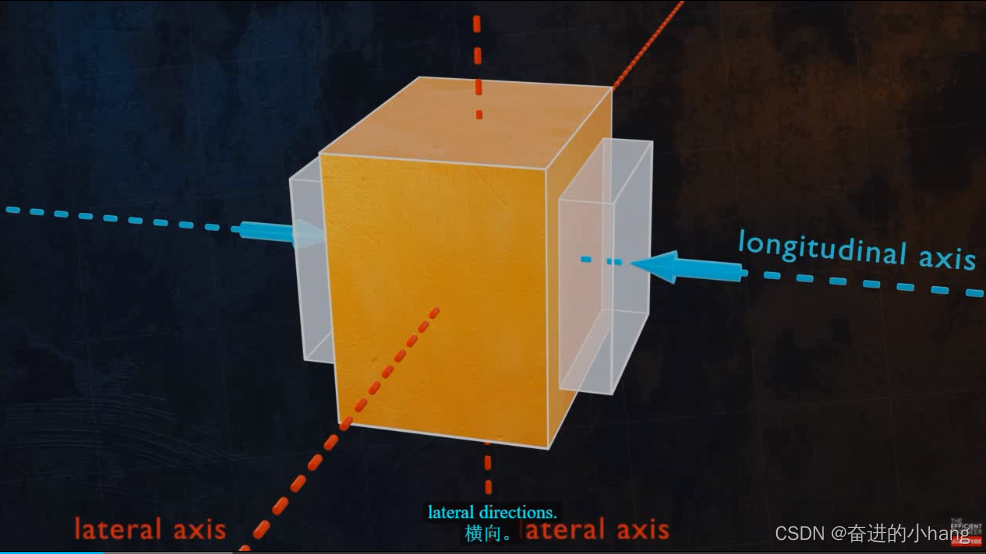
当在一个方向对材料施加载荷时,材料也会在横向上变形。 泊松比是告诉我们材料在横向会变形多少的参数。
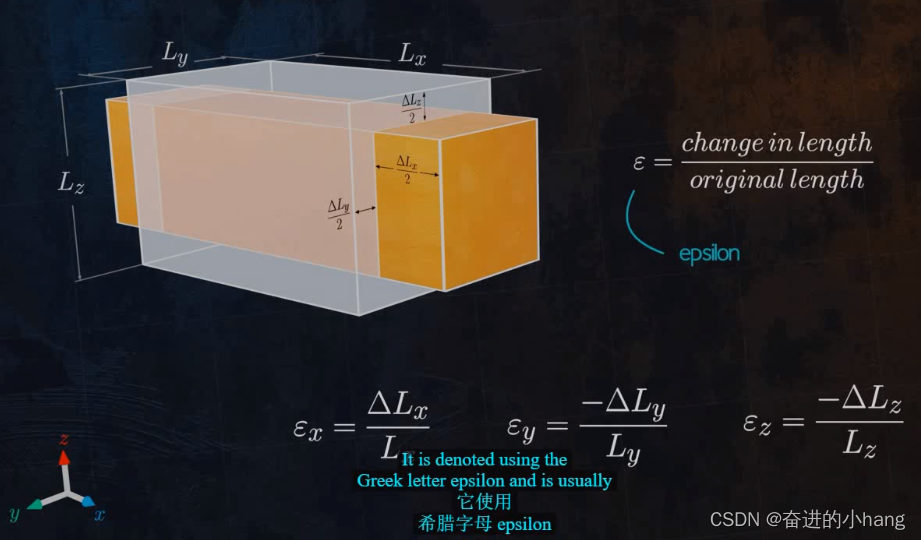
当施加纵向载荷时,结果表明横向产生的应变是相等的,它们与纵向应变成正比,横向应变与纵向应变之比实际上是一个材料常数。
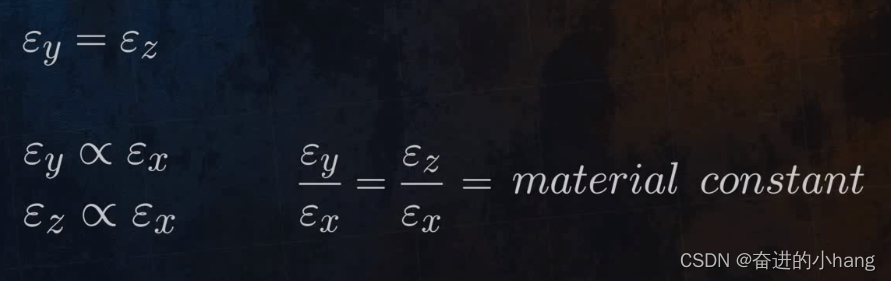
此材料常数即为泊松比(法国著名数学家Simeon Denis Poisson提出)

为什么在等式中加入一个减号?
因为按照国际惯例,拉伸应变为正,压缩应变为负
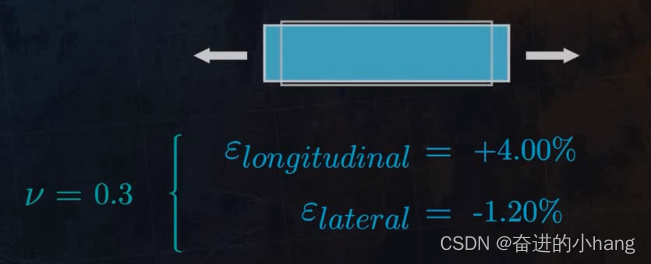
对于横向应变与纵向应变符号相反的典型情况,我们得到正泊松比
上述方程及概念仅适用于各向同性材料(isotropic),这些材料在所有方向上都具有相同的属性,同时假设材料在弹性区变形,当涉及塑性变形时,事情会变得得更加复杂

泊松比是一个无量纲的材料属性,它告诉我们,当我们在纵向上拉动材料时,它会在横向上收缩多少。
泊松比的理论值范围为-1.0-0.5,在实践中,大多数真实材料的泊松比介于0-0.5之间,大多数金属的泊松比约为0.3
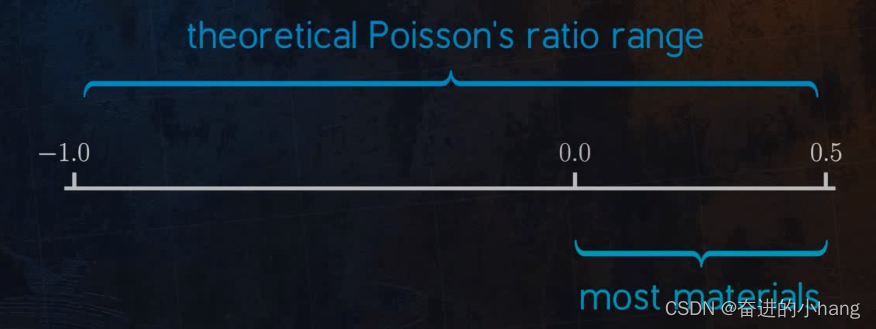
以下是一些选定材料的典型值:
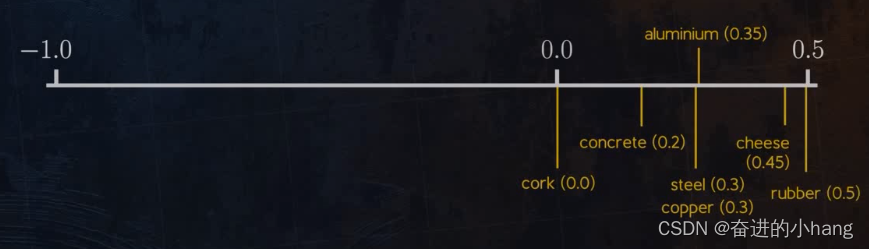
下面看看泊松比的不同值如何影响材料在荷载下的变形,
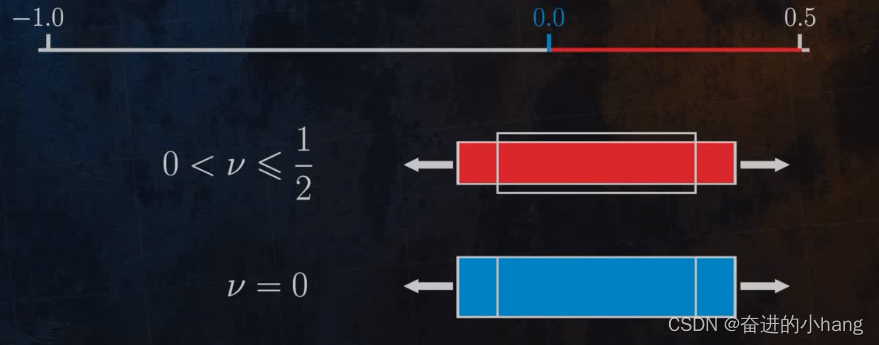
泊松比为0时,施加纵向拉力,横向没有变形,以这种方式表现的一种材料是软木(cork),这种特性使其成为某些应用中非常有用的材料。例如葡萄酒的软木塞,在压缩时不会横向膨胀,

此外还有负泊松比的材料,

这些称为拉胀材料,它们在拉动时横向膨胀,压缩时横向收缩。这些大多是工程材料,如特殊泡沫,而不是自然界中自然产生的材料。
下图显示了如何获得负泊松比,
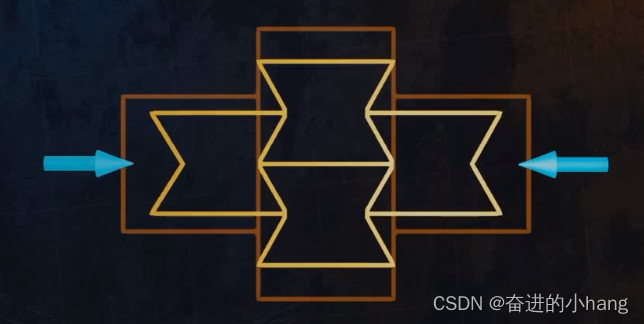
可见材料被压缩,其纵向和横向尺寸都减少了。
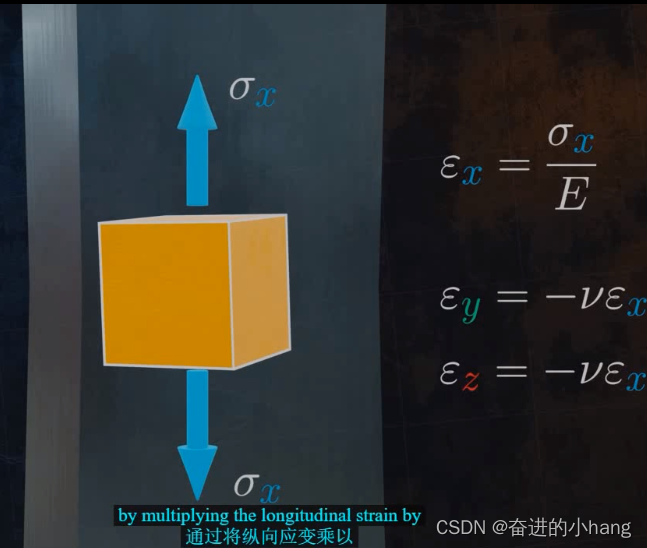
泊松比是连续介质力学中一个非常重要的参数,用于确定物体如何响应施加的应力,下面是一个单轴拉伸案列,

纵向X方向的应变(
σ
x
\sigma _x
σx )由胡克定律给出,即
σ
x
\sigma _x
σx /E,横向应变是纵向应变乘以泊松比得到的。
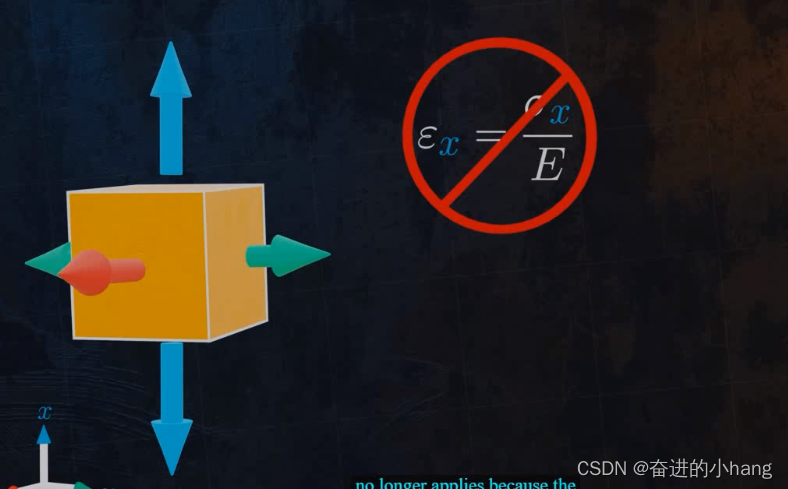
但三轴应力(tri-axial stress),在三个方向都有应力,这种情况下,不能只用胡克定律(Hooke’s law)来确定横向应变,因为还会受到Y和Z方向应变的影响。
一个方向上的应变将取决于施加在所有三个方向上的应力,我们可以使用胡克定律,结合泊松比方程和叠加原理得到,应变方程,如X方向:
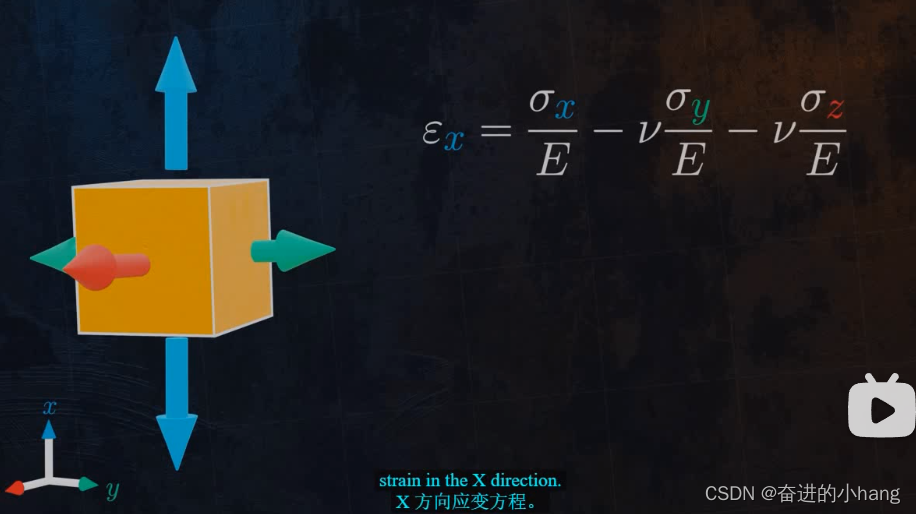
将这个方程重新排列成更实用的形式,如下:
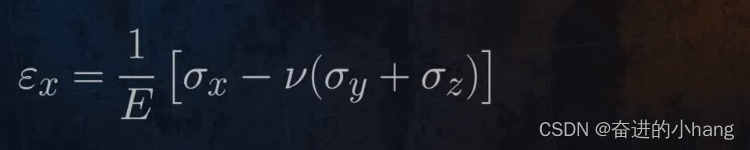
同样获得Y和Z方向的应变方程:
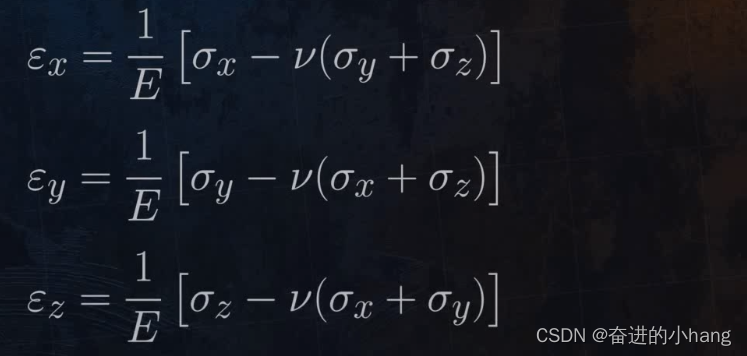
这些方程构成了广义的胡克定律(Generalised Hook’s law),可用于确定三轴应力情况下的变形。
体积应变是负载下物体体积变化的量度,可以将三个方向的应变相加来计算体积应变。使用广义胡克定律的方程来扩展体积应变方程:

下面讨论泊松比理论范围内的最大值,即
μ
\mu
μ=0.5情况下的材料,将
μ
\mu
μ=0.5带入体积应变方程,可以得到
e
v
\ e_v
ev =0,这意味着泊松比为0.5的材料,材料的体积在变形时保持不变,这些被称为不可压缩材料(incompressible materials)。

橡胶就是不可压缩材料的一个例子。
参考此链接
泊松比、泊松比范围、广义胡克定律、体积应变方程
news2026/2/10 9:20:08
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/746436.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
RK3568平台开发系列讲解(编解码篇)编解码功能介绍及体验
🚀返回专栏总目录 文章目录 一、编解码功能简介二、音频和视频播放的操作2.1、使用 gplay 播放器播放视频和音频2.2、使用 gst-launch 播放视频2.3、使用 gst-launch 播放音频2.4、使用 gst-launch 播放视频和音频沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇…
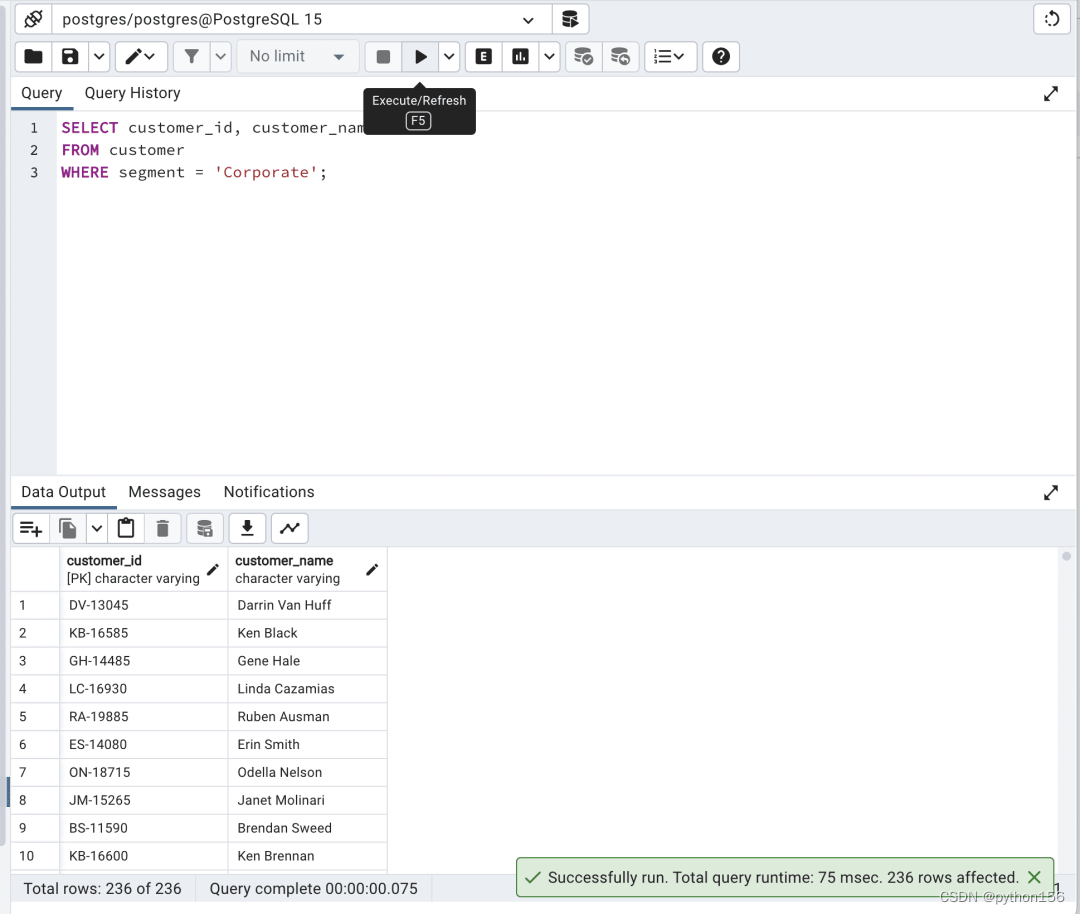
优化SQL查询实现高效数据检索(二)
大家好,本文将接着上文,继续介绍SQL查询优化的重要性以及如何优化SQL查询以实现更快的数据检索。
适当使用通配符
适当使用通配符对于优化SQL查询尤为重要,特别是在匹配字符串和模式方面。通配符是用于SQL查询中查找特定模式的特殊字符&…
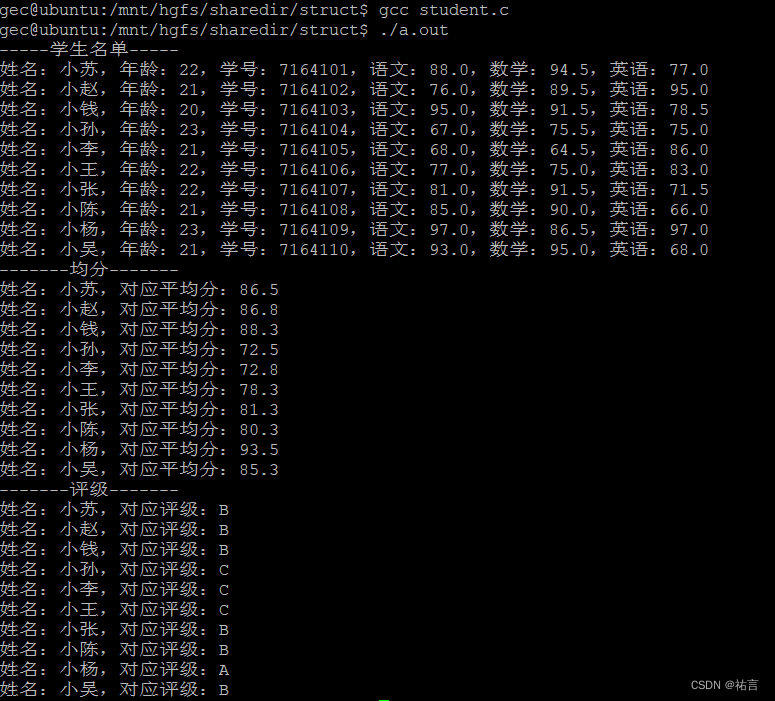
【学生系统】基于结构体的一个训练小项目
(꒪ꇴ꒪ ),hello我是祐言博客主页:C语言基础,Linux基础,软件配置领域博主🌍快上🚘,一起学习!送给读者的一句鸡汤🤔:集中起来的意志可以击穿顽石!作者水平很有限,如果发现错误&#x…
Go []uint8和string的爱恨情仇
先上代码:
package mainimport "fmt"func main() {byteSlice : []uint8{52, 44, 51} // 示例字节切片str : string(byteSlice)fmt.Printf("byteSlice:%v\r\n", str)
}// 执行-输出
byteSlice:4,3 干货:
在Go语言中,[]u…
TiDB-学习笔记02
编写这个笔记,希望能记录下学习TiDB时候的知识点。 参考文章
目的链接&详细TiDB中文手册 Overview 面板重要监控指标详解 | PingCAP 文档中心 第二章 章节Overview 面板重要监控指标详解 | PingCAP 文档中心 认识Grafana
Grafana监控TiDB 对应中文手册的【14…
如何使用 Java 代理插件在不更改应用程序代码的情况下捕获自定义指标
作者:Jack Shirazi Elastic APM Java 代理会自动跟踪许多指标,包括通过 Micrometer 或 OpenTelemetry Metrics API 生成的指标。 因此,如果你的应用程序(或其包含的库)已公开来自这些 API 之一的指标,则安装…
3Ds max无需插件创建逼真的草地
推荐: NSDT场景编辑器助你快速搭建可二次开发的3D应用场景 最终图像: 步骤-1
创建一个宽度 x 高度为 100100(我使用厘米)和 100100 段的平面。 步骤-2
将平面转换为“编辑多边形”并选择所有顶点(Ctrl A)…
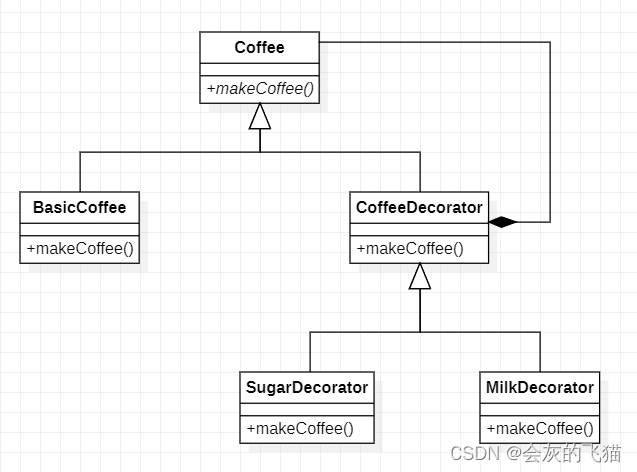
AI Chat 设计模式:6. 装饰模式
本文是该系列的第六篇,内容采用问答式的方式展开,问题由我提出,答案由 Chat AI 作出,灰色背景的文字则主要是我的旁白。 问题列表 Q.1 你知道装饰模式吗A.1Q.2 详细说说装饰模式的组成角色A.2Q.3 举一个装饰模式的例子吧…
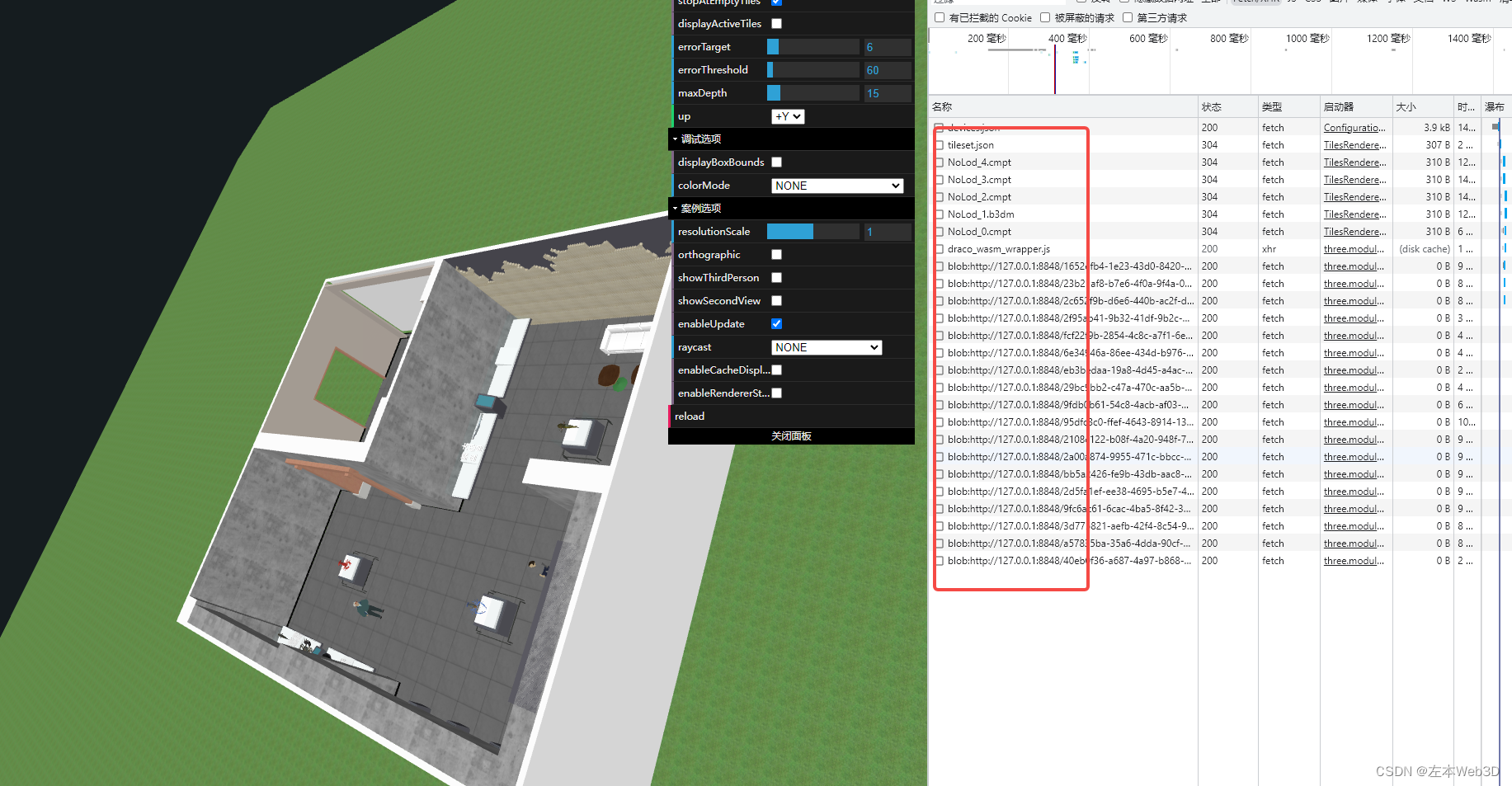
Threejs加载倾斜摄影OSGB数据
个人主页: 左本Web3D,更多案例预览请点击》 在线案例 个人简介:专注Web3D使用ThreeJS实现3D效果技巧和学习案例 💕 💕积跬步以至千里,致敬每个爱学习的你。获取模型或源码请点赞收藏加留言,有问…
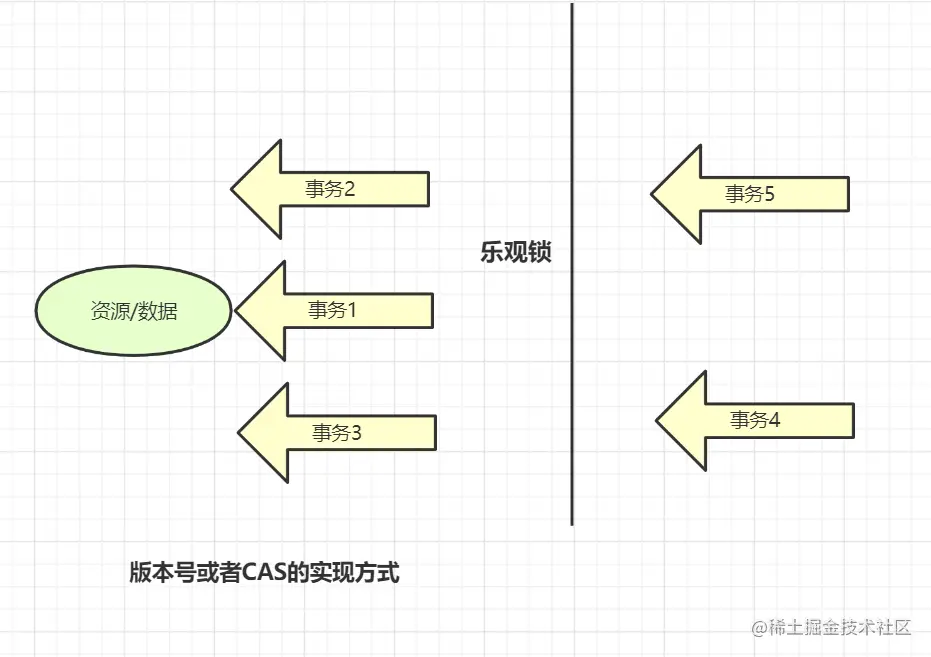
数据库锁的12连问,抗住!
前言
金三银四很快就要来啦,准备了数据库锁的12连问,相信大家看完肯定会有帮助的。 1. 为什么需要加锁 在日常生活中,如果你心情不好想静静,不想被比别人打扰,你就可以把自己关进房间里,并且反锁。这就是生…
git基础教程(linux)
1.git简介
git 分布式版本控制 git两大特点: 版本控制:支持多人同时开发 分布式:
2.安装与配置
安装
sudo apt-get install git安装成功,运行如下命令:
git3.创建一个版本库
(1)新建一个目录git_test,…
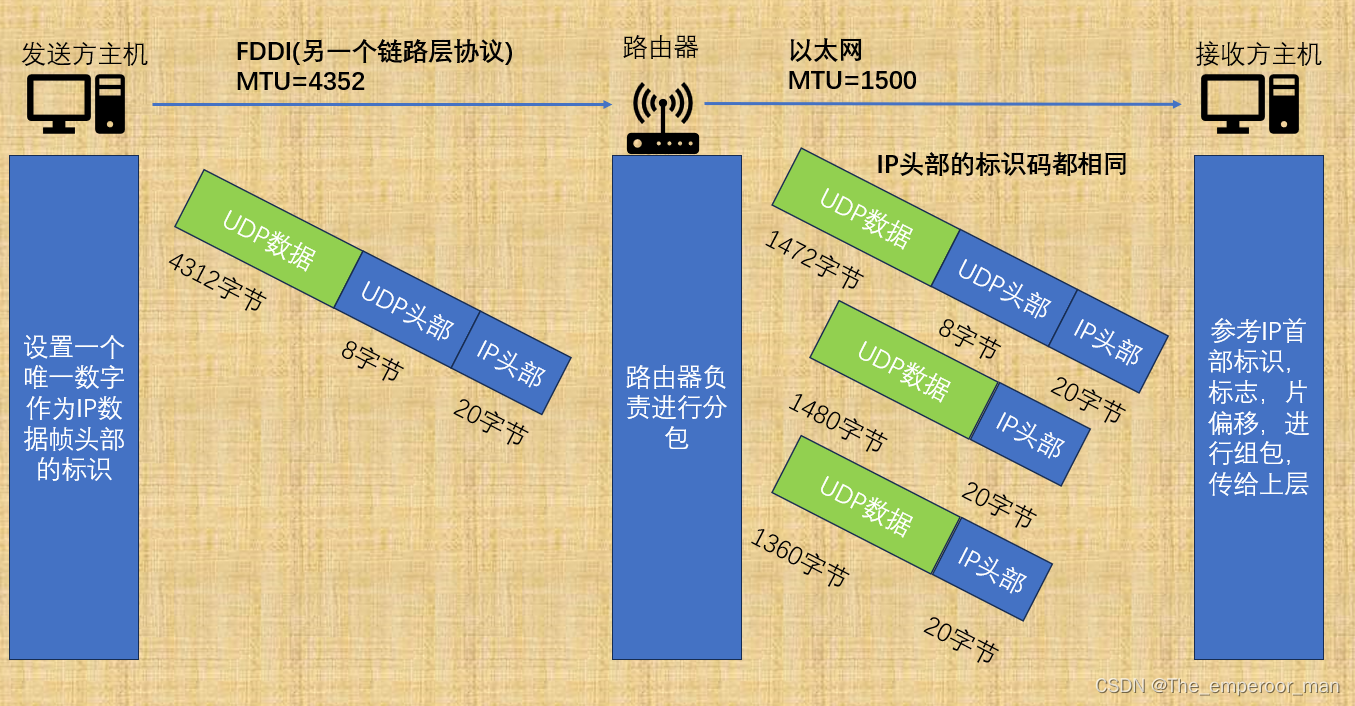
网络编程7——IP协议(子网掩码,NAT机制,IPv6协议) + 以太网
文章目录 前言一、IP协议协议头格式认识IP地址格式组成子网掩码 地址管理1.动态分配2.NAT机制3.IPv6协议 路由选择 二、以太网以太网帧格式认识MTU 总结 前言
本人是一个普通程序猿!分享一点自己的见解,如果有错误的地方欢迎各位大佬莅临指导,如果你也对编程感兴趣的话&#x…
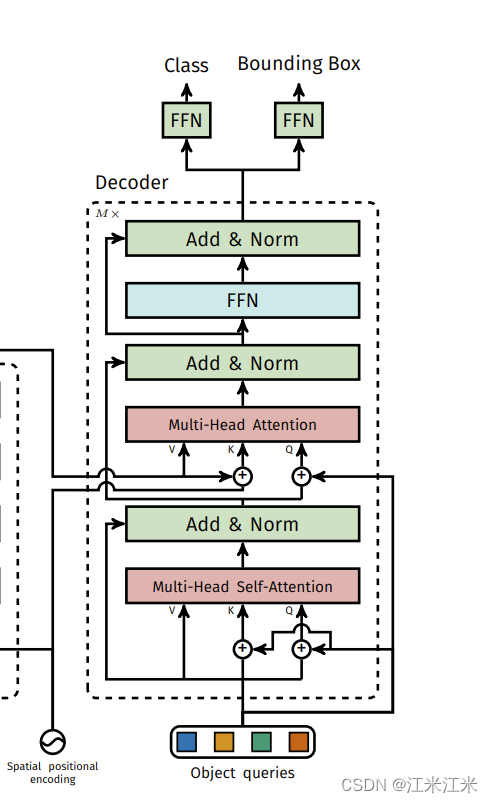
第十六章 原理篇:DETR
脑子不好使啊!复习过的东西过几天就忘记了! 参考教程: 论文地址:[pdf]End-to-End Object Detection with Transformer 源码地址:https://github.com/facebookresearch/detr 文章目录 概述the DETR modelDETR architect…
springboot篮球论坛系统
篮球论坛管理方面的任务繁琐,以至于每年都在篮球论坛管理这方面投入较多的精力却效果甚微,篮球论坛系统的目标就是为了能够缓解篮球论坛管理工作方面面临的压力,让篮球论坛管理方面的工作变得更加高效准确。 本项目在开发和设计过程中涉及到原理和技术有: B/S、java技术和MySQL…
Git❀详细使用教程
Git❀详细使用教程 一、Git简介1.1 什么是Git?1.2 Git的特点1.3 集中式与分布式的区别?1.4 Git工作流程图 二、Git安装与常用命令2.1 Git环境配置2.1.1 下载与安装2.1.2 基本配置2.1.3 为常用指令设置别名(可选)2.1.4 解决GitBash…
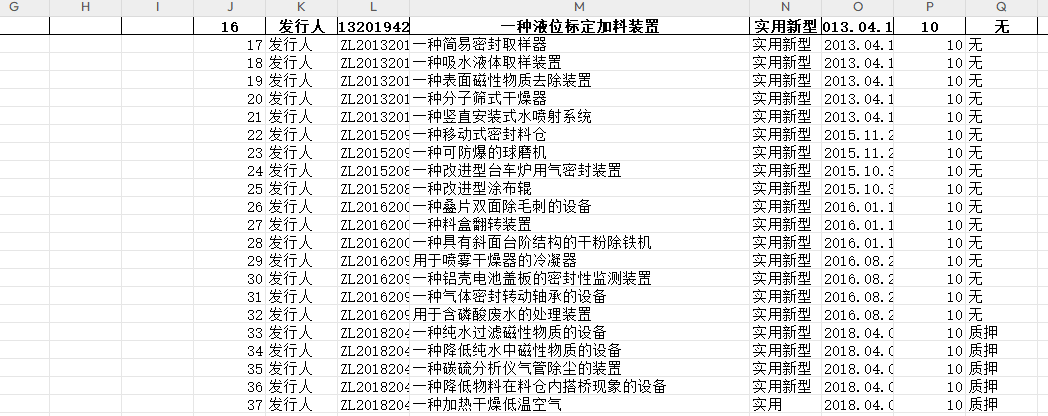
ChatGPT炒股:从上市公司招股说明书中批量提取发明专利表格
上市公司招股说明书通常会详细列明公司的发明专利,而通过企业的发明专利可以了解企业未来的业务布局情况,怎么把这些发明专利列表都批量提取出来呢? 随机打开几个上市公司的招股说明书,可以看到发明专利这一内容,共同的特征是都有…
Python的面向对象从入门到精通(简单易懂)
目录
1 初识对象
2. 成员方法 3. 类和对象
4. 构造方法
5. 其它内置方法
6. 封装
7. 继承 8. 复写
9. 类型的注解
10. 多态 1 初识对象
1. 生活中或是程序中,我们都可以使用设计表格、生产表格、填写表格的形式组织数据 2. 进行对比,在程序中&a…
进程间通信-无名管道
#include <stdio.h>
#include <unistd.h>
#include <sys/types.h>
#include <string.h>
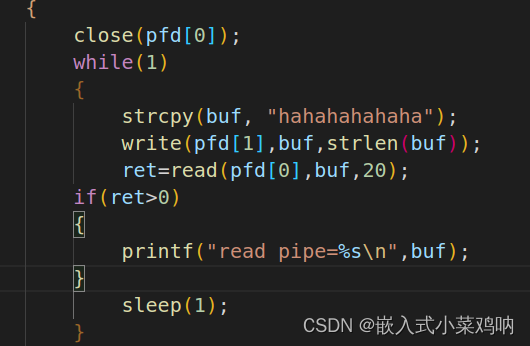
int main(int argc, char **argv)
{int pfd[2];int ret;pid_t pid;char buf[20]{0};retpipe(pfd);//创建一个无名管道if(ret<0){perror("pipe");ret…
lombok和guava工具
写在前面
本文看下如何通过使用lombok和guava来提高生产力。
1:lombok
我们开发程序时,如read method,write method,tostring,构造函数等,其写法其实都是固定和重复的,因此就可以考虑使用程序…
如何操作MySQL数据库基本数据
目录
一、MySQL数据库概念
数据
表(数据表)
数据库
数据库管理系统
数据库的建立和维护功能
数据定义功能
数据操纵功能
数据库的运行管理功能
通信功能
数据流向
二、主流数据库分类
1.SQL Server 数据库 (微软分公司产品&…

![Go []uint8和string的爱恨情仇](https://img-blog.csdnimg.cn/76e0cc7413d9439eb73fd48634dfc7bf.jpeg)