前言
🥰在学数据结构的第一节课就知道了数据结构课程是要管理并且学会操作数据,当然操作数据首先想到的就是数据的排序,排过顺序的数据的使用价值才够大。前面我们学习了顺序表也学习了链表等等,这些就是储存数据的方法,下面我们来看一看传说中的归并排序的特点与效率怎么样。😍
归并排序
| 中文名 | 归并排序 |
| 外文名 | Merge Sort |
| 发明者 | 约翰·冯·诺伊曼 |
| 稳定性 | 稳定 |
| 时间复杂度 | O(n log n) |
| 空间复杂度 | T(n) |
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
算法思路
归并排序算法有两个基本的操作,一个是分,也就是把原数组划分成两个子数组的过程。另一个是治,它将两个有序数组合并成一个更大的有序数组。
将待排序的线性表不断地切分成若干个子表,直到每个子表只包含一个元素,这时,可以认为只包含一个元素的子表是有序表。
将子表两两合并,每合并一次,就会产生一个新的且更长的有序表,重复这一步骤,直到最后只剩下一个子表,这个子表就是排好序的线性表。
归并操作的工作原理如下(非递归形式):
第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针超出序列尾将另一序列剩下的所有元素直接复制到合并序列尾
如下图所示 初始的数组是{ 16, 17, 13, 10, 9, 15, 3, 2, 5, 8, 12, 1, 11, 4, 6 }排序过程如下:
下面还有动图的演示初始数据为{ 3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48 }排序的详细过程。
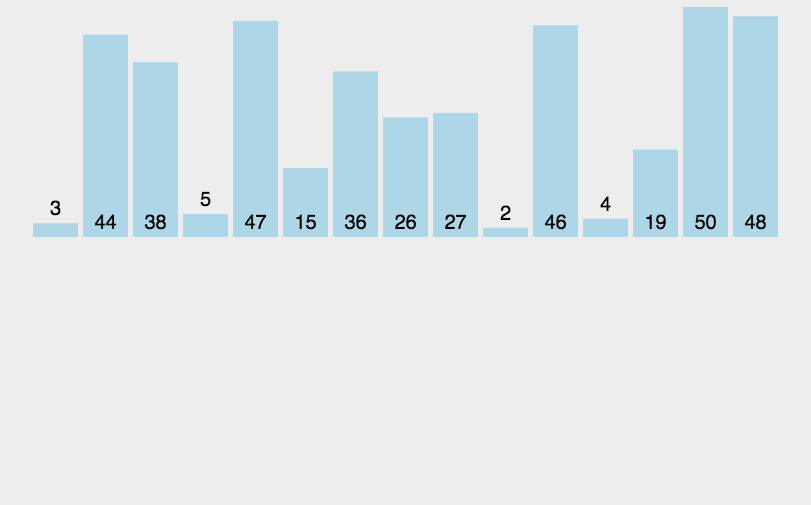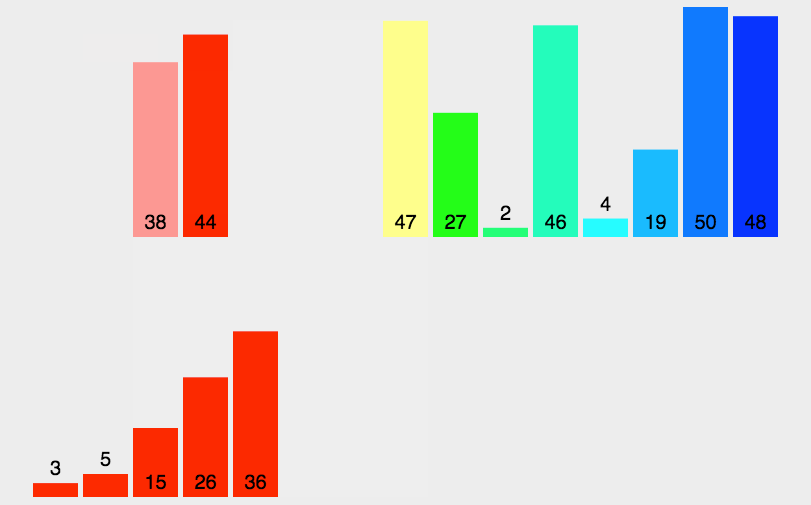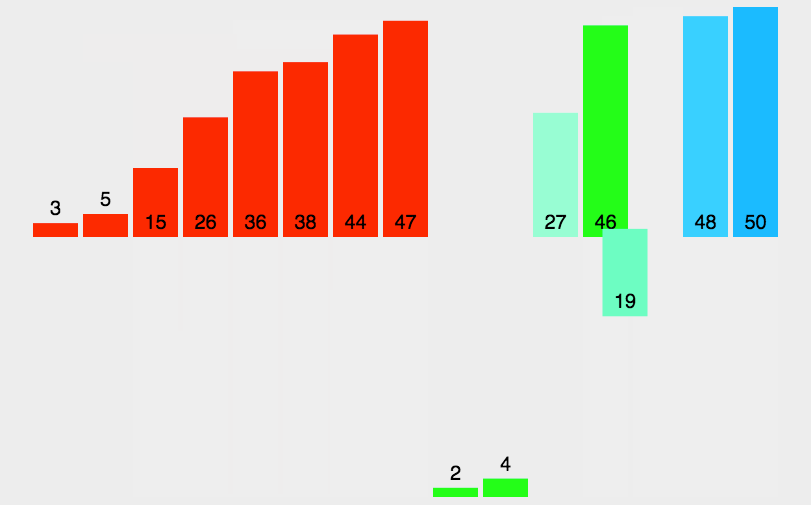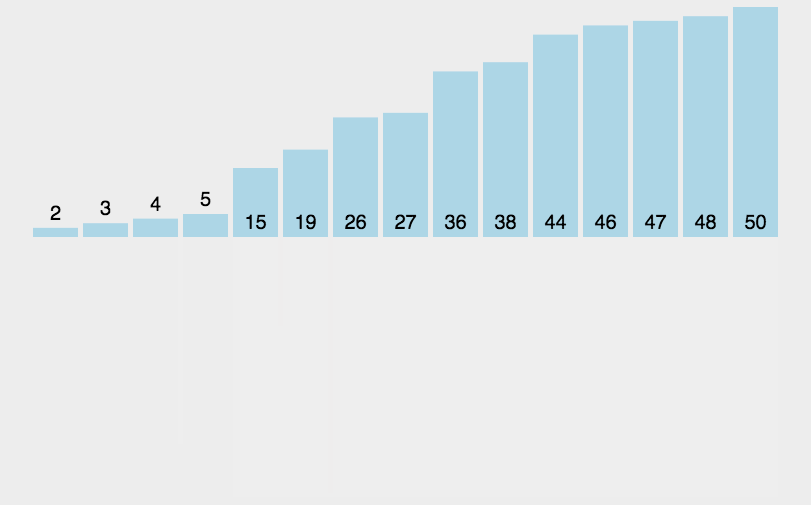
递归代码
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
// [begin, mid] [mid+1, end] 分治递归,让子区间有序
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//归并 [begin, mid] [mid+1, end]
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
// 把归并数据拷贝回原数组
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}非递归代码
类型一(修正边界法)
void MergeSortNonR1(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
// [i,i+gap-1][i+gap, i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;
end2 = n - 1;
}
else if(begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
else if(end2 >= n)
{
end2 = n - 1;
}
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
memcpy(a, tmp, sizeof(int) * n);
gap *= 2;
}
free(tmp);
}类型二(越界跳出归并法)
void MergeSortNonR2(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
//printf("gap=%d->", gap);
for (int i = 0; i < n; i += 2 * gap)
{
// [i,i+gap-1][i+gap, i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// end1越界或者begin2越界,则可以不归并了
if (end1 >= n || begin2 >= n)
{
break;
}
else if (end2 >= n)
{
end2 = n - 1;
}
int m = end2 - begin1 + 1;
int j = begin1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * m);
}
gap *= 2;
}
free(tmp);
}总结
归并排序和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。