智能优化算法——哈里鹰算法（Matlab实现）

news2024/11/26 21:48:00

目录

1 算法简介

2 算法数学模型

2.1.全局探索阶段

2.2 过渡阶段

2.3.局部开采阶段

3 求解步骤与程序框图

3.1 步骤

3.2 程序框图

4 matlab代码及结果

4.1 代码

4.2 结果

1 算法简介

哈里斯鹰算法(Harris Hawks Optimization，HHO)，是由Ali Asghar Heidari和Seyedali Mrjaili于2019年提出的一种新型仿生智能优化算法。该算法模仿哈里斯鹰捕食特点，结合Levy飞行(Levy Flights）实现对复杂多维问题求解。研究表明该新型算法具有良好的性能。在HHO中，哈里斯鹰是候选解，猎物随迭代逼近最优解．HHO算法包括两个阶段:全局探索阶段、局部开采阶段.

2 算法数学模型

2.1.全局探索阶段

在这一阶段中，哈里斯鹰处于等待状态。仔细检查和监控搜索空间[b , ub]以发现猎物。根据两种策略在随机的地方寻找猎物，迭代时以概率q进行位置更新。数学表达式如下:

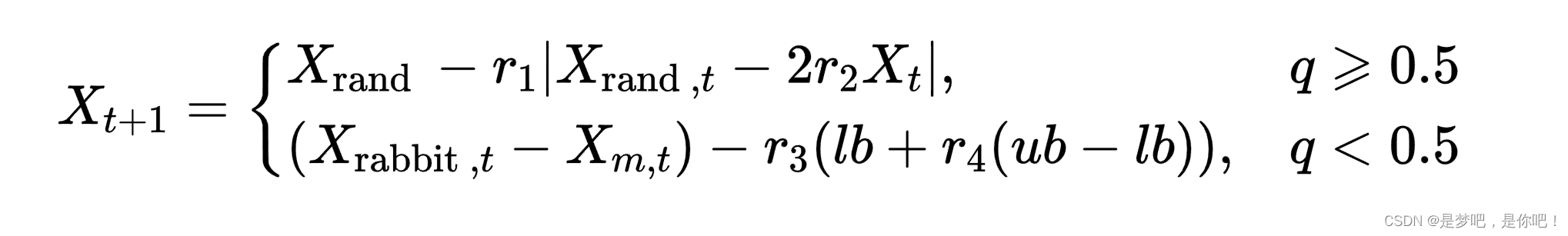
式中，

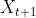
和

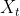
编辑分别为哈里斯鹰第t+1次和第t次迭代时的位置，Xrabbit，t表示猎物第t次迭代时的位置，q和r1，r2，r3，r4是区间(0,1)内的随机数字，lb是搜索空间的下界，ub是搜索空间的上界，Xrand，t表示第t次迭代时哈里斯鹰的随机位置，Xm，t表示第t次迭代时哈里斯鹰的平均位置，公式如下:

2.2 过渡阶段

该阶段用于保持探索和开采之间适当的平衡。HHO通过猎物的能量方程实现从探索到开采的过渡。

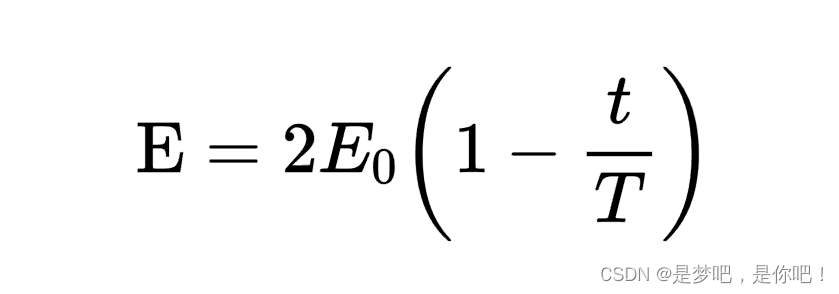
式中，E表示猎物逃跑的能量，

编辑是猎物能量的初始状态，公式为E0= 2*rand - 1，rand是(0，1)之间的随机数字,T为最大迭代次数，t为当前迭代次数.当E≥1时，哈里斯鹰算法将执行全局探索;否则，HHO算法进入局部开采。

2.3.局部开采阶段

根据猎物的逃跑行为和哈里斯鹰的追逐策略，HHO算法提出了四种可能的策略来模拟攻击行为．用N表示猎物成功逃脱的概率。

(1)软围攻.当E≥0.5，A≥0.5时，猎物有足够的能量且以跳跃的方式逃脱围捕，而哈里斯鹰会逐渐消耗猎物的能量，然后选择最佳的位置突袭俯冲逮捕猎物．更新位置的方程如下:

式中，Xt是迭代时猎物与哈里斯鹰的位置之差，J=2(1-r5）表示猎物逃跑过程中的随机跳跃，r5是介于0到1之间的随机数字.

(2)硬围攻．当E<0.5，入≥0.5时，猎物筋疲力尽，哈里斯鹰选择迅速突袭．位置更新如下：

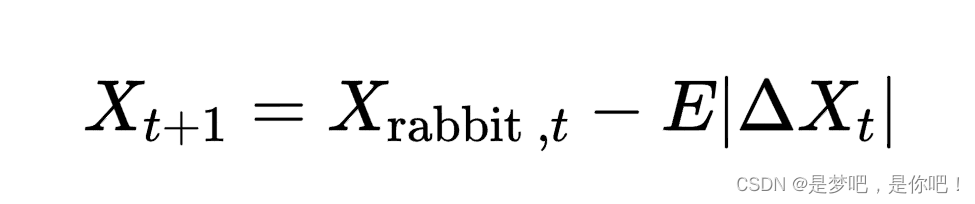
（3)累速俯冲式软围攻.当E>0.5，入<0.5时，猎物有足够的能量E逃跑，哈里斯鹰在突袭之前会建立一个软围攻.为了模拟猎物的逃跑模式和跳跃动作，将levy函数LF集成在HHO算法中．更新位置的策略为:

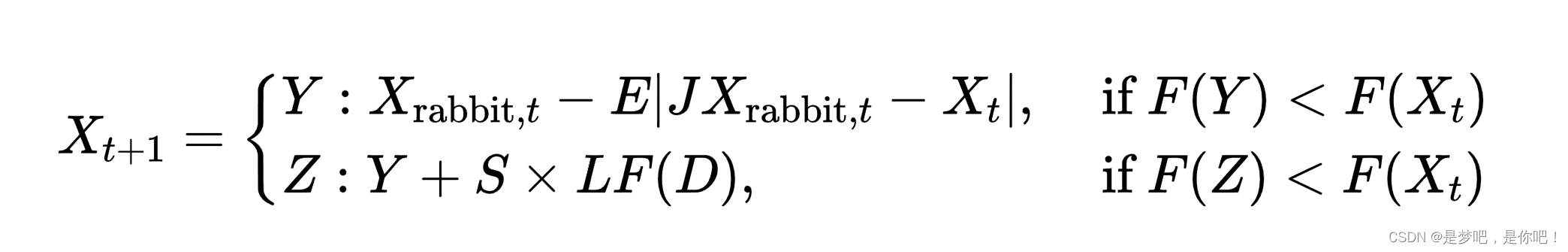
式中，D为问题维度，S为D维随机行向量.

(4)累速俯冲式硬围攻.当E<0.5，入<0.5时，猎物能量E低，哈里斯鹰在突袭前构建硬围攻捕捉猎物，位置更新如:

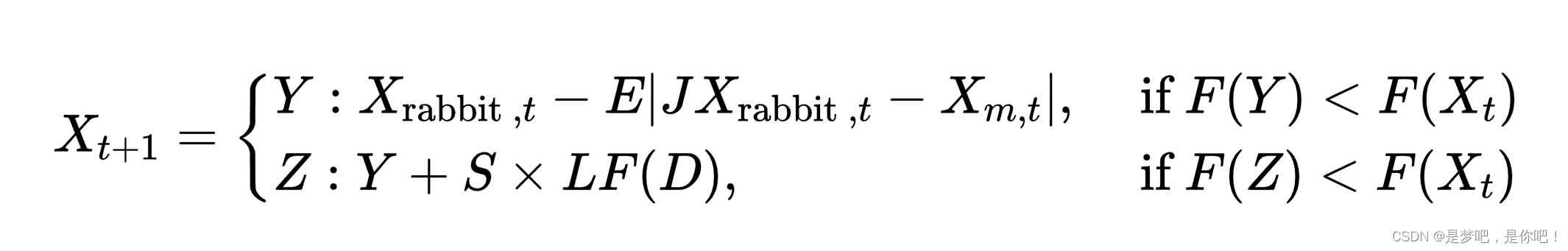
Levy飞行函数公式如下:

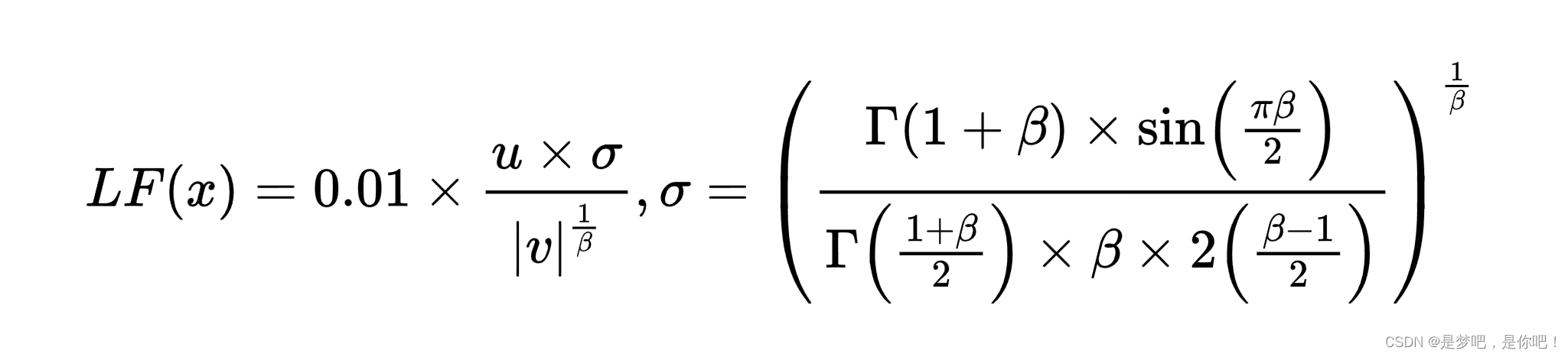
式中，u、v是(0,1)之间的随机数，β取常值1.5。

HHO算法用猎物能量E和因子入调节哈里斯鹰和猎物（兔子)之间的四种围捕机制，来实现优化求解问题.

3 求解步骤与程序框图

3.1 步骤

HHO算法的规则描述如下:
1)每次迭代前，判断是否越界并调整，更新猎物位置与适应度值;
2)在搜索阶段，哈里斯鹰拥有两种不同搜索方式，分别针对发现和未发现猎物;
3)野兔的逃逸能量会随着迭代次数增加而自适应减小;
4)当野兔能量降低到某一阈值，将被哈里斯鹰群发现，狩猎从搜索阶段转为围捕突袭阶段;
5)每一次突袭前，兔子都有一定的概率从包围中逃脱;
6)针对兔子的体力，以及是否逃脱包围圈，哈里斯鹰有四种不同的围捕策略;
7）每次围捕最终兔子将会捕获，每次迭代会产生一个新的猎物，该位置将由新一代种群中适应度值最优者占据。
实现步骤
Step1:初始化种群:包括搜索空间的上限和下限，算法的最大迭代次数T。随机初始化种群位置.
Step2:根据适应度函数计算每个个体的适应度值，保存种群最优个体.
Step3:更新猎物逃逸能量E.
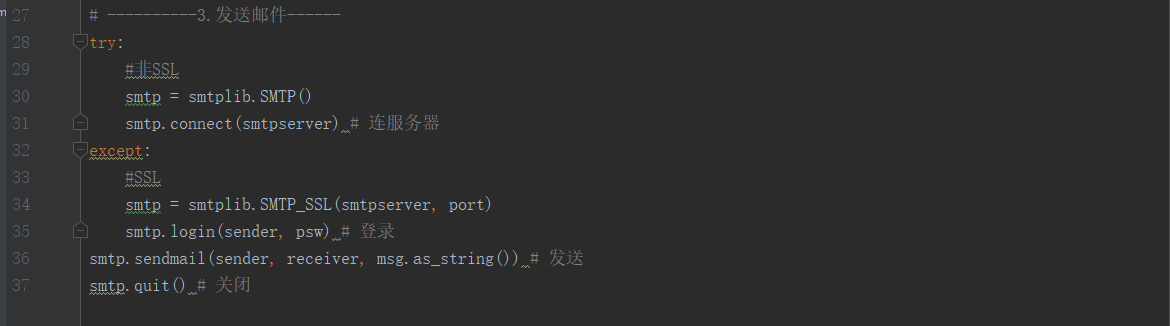
Step4:比较E的大小，按位置更新公式或四种策略追捕猎物，更新位置.Step5:对每个个体，计算适应度，更新种群最优的适应度值.
Step6:判断搜索到的结果是否满足停止条件(达到最大迭代次数或满足精度要求)，若满足停止条件则输出最优值，否则转到Step3继续运行直到满足条件为止.

3.2 程序框图

4 matlab代码及结果

4.1 代码

%% 智能优化算法——哈里鹰算法（Matlab实现）
clear
close all
clc
 
SearchAgents_no = 30 ; %　种群规模
dim = 10 ; % 粒子维度
Max_iter = 1000 ; %　迭代次数
ub = 5 ;
lb = -5 ;
%% 初始化猎物位置和逃逸能量
Rabbit_Location=zeros(1,dim);
Rabbit_Energy=inf;
 
%% 初始化种群的位置
Positions= lb + rand(SearchAgents_no,dim).*(ub-lb) ;
 
Convergence_curve = zeros(Max_iter,1);
 
%% 开始循环
for t=1:Max_iter
    for i=1:size(Positions,1)
        % Check boundries
        FU=Positions(i,:)>ub;FL=Positions(i,:)<lb;Positions(i,:)=(Positions(i,:).*(~(FU+FL)))+ub.*FU+lb.*FL;
        % fitness of locations
        fitness=sum(Positions(i,:).^2);
        % Update the location of Rabbit
        if fitness<Rabbit_Energy
            Rabbit_Energy=fitness;
            Rabbit_Location=Positions(i,:);
        end
    end
    
    E1=2*(1-(t/Max_iter)); % factor to show the decreaing energy of rabbit
    %% Update the location of Harris' hawks
    for i=1:size(Positions,1)
        E0=2*rand()-1; %-1<E0<1
        Escaping_Energy=E1*(E0);  % escaping energy of rabbit
        
        if abs(Escaping_Energy)>=1
            %% Exploration:
            % Harris' hawks perch randomly based on 2 strategy:
            
            q=rand();
            rand_Hawk_index = floor(SearchAgents_no*rand()+1);
            X_rand = Positions(rand_Hawk_index, :);
            if q<0.5
                % perch based on other family members
                Positions(i,:)=X_rand-rand()*abs(X_rand-2*rand()*Positions(i,:));
            elseif q>=0.5
                % perch on a random tall tree (random site inside group's home range)
                Positions(i,:)=(Rabbit_Location(1,:)-mean(Positions))-rand()*((ub-lb)*rand+lb);
            end
            
        elseif abs(Escaping_Energy)<1
            %% Exploitation:
            % Attacking the rabbit using 4 strategies regarding the behavior of the rabbit
            
            %% phase 1: surprise pounce (seven kills)
            % surprise pounce (seven kills): multiple, short rapid dives by different hawks
            
            r=rand(); % probablity of each event
            
            if r>=0.5 && abs(Escaping_Energy)<0.5 % Hard besiege
                Positions(i,:)=(Rabbit_Location)-Escaping_Energy*abs(Rabbit_Location-Positions(i,:));
            end
            
            if r>=0.5 && abs(Escaping_Energy)>=0.5  % Soft besiege
                Jump_strength=2*(1-rand()); % random jump strength of the rabbit
                Positions(i,:)=(Rabbit_Location-Positions(i,:))-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Positions(i,:));
            end
            
            %% phase 2: performing team rapid dives (leapfrog movements)
            if r<0.5 && abs(Escaping_Energy)>=0.5% Soft besiege % rabbit try to escape by many zigzag deceptive motions
                
                Jump_strength=2*(1-rand());
                X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Positions(i,:));
                
                if sum(X1.^2)<sum(Positions(i,:).^2) % improved move
                    Positions(i,:)=X1;
                else % hawks perform levy-based short rapid dives around the rabbit
                    %Levy flight
                    beta=1.5;
                    sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
                    u=randn(1,dim)*sigma;v=randn(1,dim);step=u./abs(v).^(1/beta);
                    o1=0.01*step;
                    X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-Positions(i,:))+rand(1,dim).*o1;
                    if (sum(X2.^2)<sum(Positions(i,:).^2))% improved move
                        Positions(i,:)=X2;
                    end
                end
            end
            
            if r<0.5 && abs(Escaping_Energy)<0.5% Hard besiege % rabbit try to escape by many zigzag deceptive motions
                % hawks try to decrease their average location with the rabbit
                Jump_strength=2*(1-rand());
                X1=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(Positions));
                
                if sum(X1.^2)<sum(Positions(i,:).^2) % improved move
                    Positions(i,:)=X1;
                else % Perform levy-based short rapid dives around the rabbit
                    %Levy flight
                    beta=1.5;
                    sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
                    u=randn(1,dim)*sigma;v=randn(1,dim);step=u./abs(v).^(1/beta);
                    o2=0.01*step;
                    X2=Rabbit_Location-Escaping_Energy*abs(Jump_strength*Rabbit_Location-mean(Positions))+rand(1,dim).*o2;
                    if (sum(X2.^2)<sum(Positions(i,:).^2))% improved move
                        Positions(i,:)=X2;
                    end
                end
            end
            %%
        end
    end
    
    Convergence_curve(t)=Rabbit_Energy;
    % Print the progress every 100 iterations
    if mod(t,50)==0
        display(['At iteration ', num2str(t), ' the best fitness is ', num2str(Rabbit_Energy)]);
    end
end
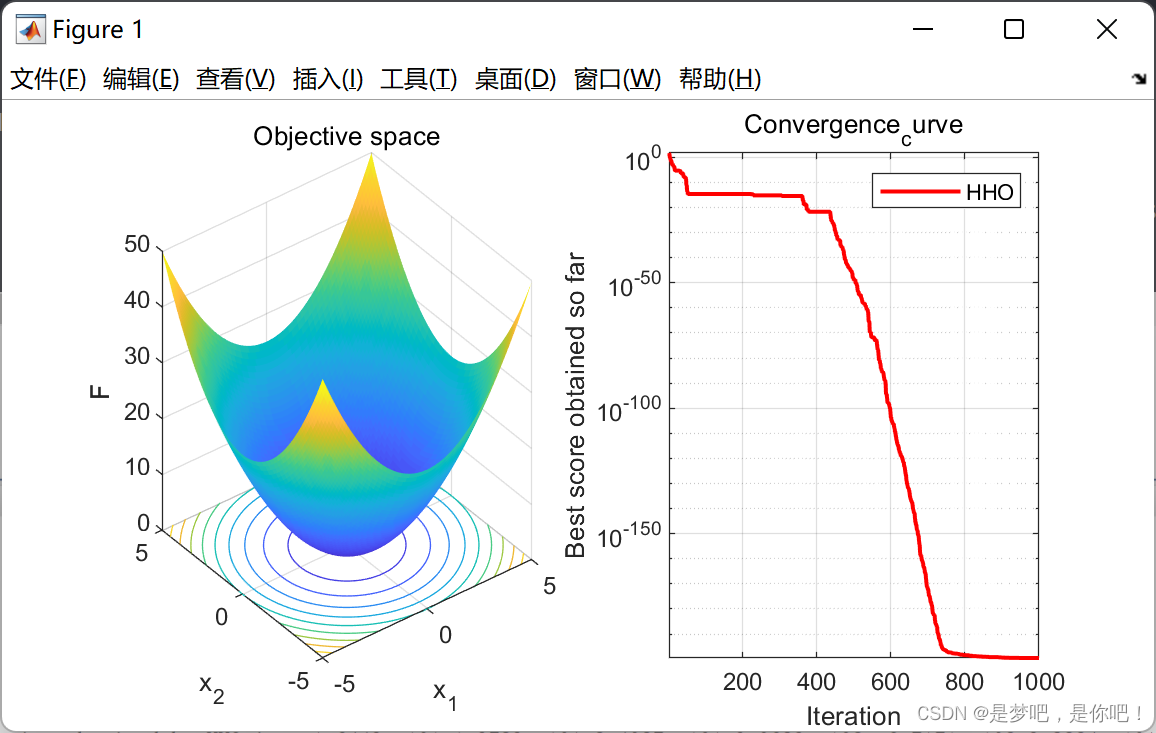
figure('unit','normalize','Position',[0.3,0.35,0.4,0.35],'color',[1 1 1],'toolbar','none')
subplot(1,2,1);
x = -5:0.1:5;y=x;
L=length(x);
f=zeros(L,L);
for i=1:L
    for j=1:L
       f(i,j) = x(i)^2+y(j)^2;
    end
end
surfc(x,y,f,'LineStyle','none');
xlabel('x_1');
ylabel('x_2');
zlabel('F')
title('Objective space')
 
subplot(1,2,2);
semilogy(Convergence_curve,'Color','r','linewidth',1.5)
title('Convergence_curve')
xlabel('Iteration');
ylabel('Best score obtained so far');
 
axis tight
grid on
box on
legend('HHO')
display(['The best solution obtained by HHO is : ', num2str(Rabbit_Location)]);
display(['The best optimal value of the objective funciton found by HHO is : ', num2str(Rabbit_Energy)]);

4.2 结果

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/746256.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

IME SoftInputWindow窗口添加

IME SoftInputWindow窗口添加

IME SoftInputWindow窗口添加 1、时序图2、InputMethodService#onCreate()3、Dialog添加到WMS android12-release1 1、时序图 输入法应用继承InputMethodServiceframeworks/base/core/java/android/view/inputmethod/InputMethodManager.java frameworks/base/core/java/andro…
阅读更多...
【JAVA】数据类型，类型转换与提升，运算符，标识符命名规则

【JAVA】数据类型，类型转换与提升，运算符，标识符命名规则

&#x1f349;内容专栏&#xff1a;【JAVA】 &#x1f349;本文脉络&#xff1a;数据类型&#xff0c;类型转换与提升&#xff0c;运算符&#xff0c;标识符命名规则 &#x1f349;本文作者&#xff1a;Melon_西西 &#x1f349;发布时间 &#xff1a;2023.7.12 目录 1. 字面常…
阅读更多...
【数据结构】数据结构的基本概念

【数据结构】数据结构的基本概念

文章目录 思维导图数据结构的基本概念和术语数据结构三要素逻辑结构存储结构数据的运算 重要知识总结 思维导图 数据结构的基本概念和术语 数据&#xff1a;数据是信息的载体。是描述客观事物属性的数、字符及所有能输入到计算机中并被计算机程序识别和处理的符号的集合。数据…
阅读更多...
【计算机视觉 | 目标检测 | 图像分割】arxiv 计算机视觉关于目标检测和图像分割的学术速递（7 月 12 日论文合集）

【计算机视觉 | 目标检测 | 图像分割】arxiv 计算机视觉关于目标检测和图像分割的学术速递（7 月 12 日论文合集）

文章目录 一、检测相关(7篇)1.1 3D detection of roof sections from a single satellite image and application to LOD2-building reconstruction1.2 Towards exploring adversarial learning for anomaly detection in complex driving scenes1.3 Unveiling the invisible: …
阅读更多...
探索嵌入式系统：初学者必知的核心概念解析

探索嵌入式系统：初学者必知的核心概念解析

探索嵌入式系统&#xff1a;初学者必知的核心概念解析 嵌入式系统是指嵌入在其他设备或系统中的特定目的的计算机系统。它们通常用于控制、监测或执行特定任务&#xff0c;例如汽车的引擎控制单元、智能手机的操作系统或家电中的微控制器。对于初学者来说&#xff0c;以下是一…
阅读更多...
Android自动化测试中如何处理各种弹窗

Android自动化测试中如何处理各种弹窗

目录 弹窗的种类: APP内的业务弹窗 弹窗处理 watcher的使用 实战案例 总结&#xff1a; 在UI自动化测试中弹窗是影响自动化用例稳定性的一大因素&#xff0c;如何方便快捷的处理各种情况下的弹窗&#xff0c;是搞UI自动化测试必须要面临的问题. 弹窗的种类: 安装APP时的…
阅读更多...
MySQL事务 | 隔离级别 | 数据一致性

MySQL事务 | 隔离级别 | 数据一致性

文章目录 简介一、事务并发问题1. 脏读&#xff08;Dirty Read&#xff09;2. 不可重复读&#xff08;Non-repeatable Read&#xff09;3. 幻读&#xff08;Phantom Read&#xff09;幻读和不可重复读的区别 二、事务隔离级别1. 回顾事务2. 事务级别3. 特点和优缺点 三、事务隔…
阅读更多...
科研笔记：一些有用的网站整理（更新中）

科研笔记：一些有用的网站整理（更新中）

1 论文整理网站 整理AI相关领域的一些综述GitHub - KaiyuanGao/AI-Surveys: 整理AI相关领域的一些综述时间序列的paper/code汇总GitHub - qingsongedu/awesome-AI-for-time-series-papers: A professional list of Papers, Tutorials, and Surveys on AI for Time Series in t…
阅读更多...
OpenSource - Spring Startup Ananlyzer

OpenSource - Spring Startup Ananlyzer

文章目录 &#x1f680;Optimization of Spring Startup核心能力&#x1f4c8;Spring应用启动数据采集报告应用启动时长优化 &#x1f4c8;Spring应用启动数据采集报告安装jar包配置项应用启动自定义扩展 &#x1f680;应用启动时长优化支持异步化的Bean类型接入异步Bean优化 开…
阅读更多...
idea配置类注解和方法注解最详细教材

idea配置类注解和方法注解最详细教材

1.配置类注释 点击setting 方法一&#xff1a; 1.按照要求添加下图中的模板 /*** Author: aaa* Date: ${YEAR}/${MONTH}/${DAY}* Description: */ 2.勾选下面的两个勾后点击apply 方法二&#xff1a; 我们看到了在刚刚那个模板中有这样一句话 这句话是表示创建项目的时候会…
阅读更多...
CASAIM与大疆达成全自动化测量技术合作，CASAIM IS全自动化蓝光测量仪实现无人机叶片全尺寸检测及质量控制

CASAIM与大疆达成全自动化测量技术合作，CASAIM IS全自动化蓝光测量仪实现无人机叶片全尺寸检测及质量控制

近期&#xff0c;CASAIM与大疆达成全自动化测量技术合作&#xff0c;CASAIM IS全自动化蓝光测量仪实现无人机叶片全尺寸检测及质量控制。 无人机行业在过去几年里取得了迅猛发展&#xff0c;大疆是全球领先的无人飞行器控制系统及无人机解决方案的研发商和生产商&#xff0c;客…
阅读更多...
2023年网页设计制作工具盘点

2023年网页设计制作工具盘点

过去&#xff0c;专业人员使用HTMLL、CSS、Javascript等代码手动编写和构建网站。现在有越来越多的智能网页制作工具来帮助任何人实现零代码基础&#xff0c;随意建立和设计网站。在本文中&#xff0c;我们将向您介绍2023年流行的网页制作工具。 1.即时设计 即时设计是一款UI…
阅读更多...
​python接口自动化（三十一）--html测试报告通过邮件发出去——下（详解）​

​python接口自动化（三十一）--html测试报告通过邮件发出去——下（详解）​

简介　 本篇总结了 QQ &#xff08;SSL&#xff09;邮箱和 163&#xff08;非SSL&#xff09; 邮箱发送邮件&#xff0c;专治各种不行&#xff0c;总之看完这篇以后麻麻再也不用担心我的邮件收不到了。以下代码兼容 python2 和 python3&#xff0c;运行无异常&#xff0c;放心大…
阅读更多...
Jmeter脚本参数化和正则匹配

Jmeter脚本参数化和正则匹配

目录 一、参数化 1.用户定义的变量 2.CSV数据文件设置 3.用户参数 二、正则提取 1.JSON提取器 2.正则表达式提取器 我们在做接口测试过程中&#xff0c;往往会遇到以下几种情况 每次发送请求&#xff0c;都需要更改参数值为未使用的参数值&#xff0c;比如手机号注册、…
阅读更多...
python爬虫_requests获取小黄人表情保存到文件夹

python爬虫_requests获取小黄人表情保存到文件夹

文章目录 ⭐前言&#x1f496; requests简介&#xff08;发送请求&#xff09;&#x1f496; urlretrieve简介&#xff08;下载远程图片&#xff09;&#x1f496; 获取图片的接口保存到本地&#x1f496; 加餐环节&#xff1a;前端vue3antd展示图片 ⭐结束 ⭐前言 大家好&…
阅读更多...
Hightopo 使用心得（4）- 3D 场景 Graph3dView 与 Obj 模型

Hightopo 使用心得（4）- 3D 场景 Graph3dView 与 Obj 模型

在前一篇文章《Hightopo 使用心得&#xff08;3&#xff09;- 吸附与锚点》中&#xff0c;我们在结尾处提到过 HT 的 3D 场景。这里我们通过代码建立一个 3D 场景并添加一个 Obj 模型来介绍一下 HT for Web 在 3D 场景和模型加载方面的使用。 这是我们最终实现的效果&#xff…
阅读更多...
vue3使用monaco-editor插件,报错Unexpected usage

vue3使用monaco-editor插件,报错Unexpected usage

在使用monaco-editor插件的时候&#xff0c;运行时没有报错&#xff0c;打开页面报如上错误&#xff0c;可以关掉&#xff0c;但是页面变了 还会再出现&#xff0c;上网找了一圈报错&#xff0c;是因为插件引入时产生的问题 原来的 import * as Monaco from monaco-editor更改…
阅读更多...
论文笔记--TinyBERT: Distilling BERT for Natural Language Understanding

论文笔记--TinyBERT: Distilling BERT for Natural Language Understanding

论文笔记--TinyBERT: Distilling BERT for Natural Language Understanding 1. 文章简介2. 文章概括3 文章重点技术3.1 Transformer Distillation3.2 两阶段蒸馏 4. 数值实验5. 文章亮点5. 原文传送门6. References 1. 文章简介 标题&#xff1a;TinyBERT: Distilling BERT fo…
阅读更多...
Java四个月学不学的会？我分享一下我的经历来告诉你

Java四个月学不学的会？我分享一下我的经历来告诉你

先说结论&#xff0c;java培训 四个月一般是能达到能上手工作的水平的&#xff0c;但是高中毕业就算了。高中毕业哪怕你能上手工作了&#xff0c;需求能完成了&#xff0c;也是大概率找不到工作的&#xff0c;这一行可能最看重学历的行业之一了。虽然说句实在话&#xff0c;就…
阅读更多...
【Linux】基础开发工具——gcc/g++篇

【Linux】基础开发工具——gcc/g++篇

文章目录 一、预处理1.1 头文件展开1.2 条件编译 二、编译三、汇编四、链接4.1 什么是库?4.2 库的分类4.3 目标文件和库是如何链接的&#xff1f;4.3.1 动态链接4.3.2 静态链接 4.4 动静态链接的优缺点对比 五、Debug&&release 前言 &#xff1a;  在前面的文章里给大…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023