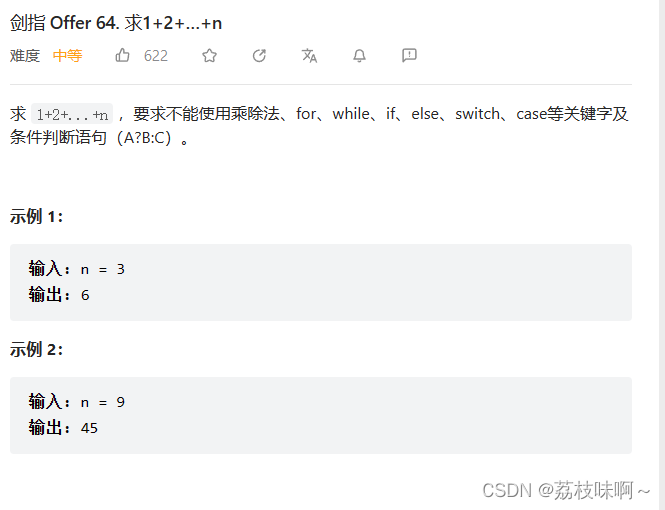
看到题脑子里就有了想法，这还不简单，直接用递归啊，return一个n+sumNums(n-1)写完之后发现到了0你得终止但是不能用if等语句你没办法终止，想了大概十分钟放弃了，这没办法终止啊，然后看了题解。

class Solution {
    public int sumNums(int n) {
       boolean flag = n > 0 && (n = sumNums(n-1) + n) > 0;
       return n;
    }
}

 解题的关键就在于当判断A&&B的时候，如果A是false，那么A&&B就确定为false就不会执行B，如果A||B，A确定是true，那么就确定A||B是true，那么就不会执行B。所以题解中当n=0的时候就不会继续递归了，最终返回的就是1+2+..+n了。题解还用了一种位运算的方法。

1+2+...+n=n(n+1)/2,除以2可以通过右移一位获得，n(n+1)可以通过俄罗斯农民乘法获得。

俄罗斯农民乘法是一种将数字转成二进制后,通过位移操作,最后将乘法转换成加法的高效算法. 原理是将被乘数除以2, 乘数乘以2, 如果被乘数除以2以后有余数 (余数为1), 则将乘数累加到结果中. 以25*20为例: 25的二进制是11001，20的二进制是10100，将20左移一位得到101000，将25右移一位得到1100，再左移一位得到11000，此时25为1，累加20，结果为11000+20=11020。但是不能用for循环，根据数据大小是1-10000，二进制展开最多14位，于是手动展开。

class Solution {
    public int sumNums(int n) {
        int ans = 0, A = n, B = n + 1;
        boolean flag;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        flag = ((B & 1) > 0) && (ans += A) > 0;
        A <<= 1;
        B >>= 1;

        return ans >> 1;
    }
}