1.股票交易
在股票买卖的最佳时机问题中，给定一个数组，数组中的每个元素代表某一天的股票价格。你可以进行多次买入和卖出，但是必须在再次购买前卖出之前的股票。目标是找到最大的利润。
动态规划可以用于解决股票交易类的问题，其中最常见的问题是股票买卖的最佳时机问题（Best Time to Buy and Sell Stock）。
2.题目
1）
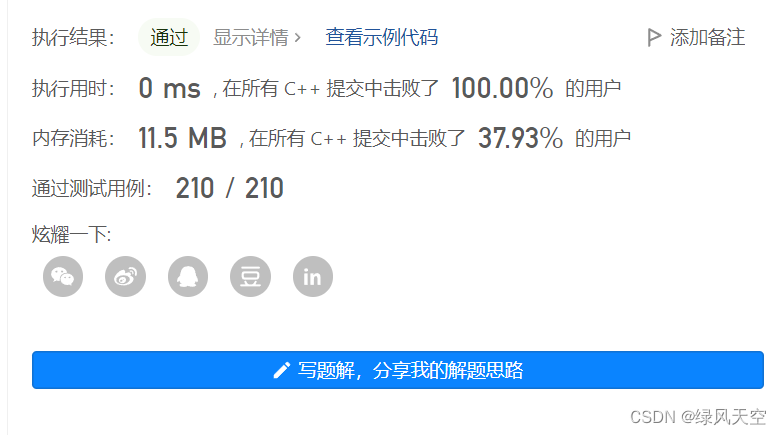
力扣
https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/找到当前位置之前的元素中的最小值，与当前位置的元素相减，遍历一维数组，找到最大差值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int minp = prices[0];
int n = prices.size();
int res = 0;
for(int i=1;i<n;i++){
res = max(res, prices[i]-minp);
minp = min(minp, prices[i]);
}
return res;
}
};2)
力扣https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/这道题的难点在于最多购买股票两次，如果一直顺序考虑股票数组，就会变得很复杂，需要记录的值很多。
所有可以顺序加逆序考虑：
顺序：找到当前位置之前的最小值，当前位置元素与之计算差值，保留最大的差值。
逆序：找到当前位置之后的最大值，最大值与当前位置元素计算差值，保留最大的差值。
这样对于每个位置，都知道了这个位置之前一次购买卖出的最大利润，和这个位置以及这个位置之后一次购买卖出的最大利润。
把这个两个值相加，得到的就是每个位置最多购买两次彩票时的最大值。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<int> dp(n,0);
int minp = prices[0];
for(int i=1;i<n;i++){
dp[i] = max(dp[i-1], prices[i]-minp);
minp = min(minp, prices[i]);
}
vector<int> dp2(n,0);
int maxp = prices[n-1];
for(int i=n-2;i>=0;i--){
dp2[i] = max(dp2[i+1], maxp-prices[i]);
maxp = max(maxp, prices[i]);
}
int res = 0;
for(int i=0;i<n;i++){
res = max(res, dp[i]+dp2[i]);
}
return res;
}
};3)
力扣https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/题解：
这题需要额外考虑完成k次交易这一因素
所以转移方程为：buy[i][j]代表遍历prices[0...i]完成j笔交易，且此刻持有一只股票的最大收益。
sell[i][j]代表遍历prices[0...i]完成j笔交易，且此刻不持有股票的最大收益。
所以buy[i][j] = max(buy[i-1][j], sell[i-1][j]-prices[i])
取只考虑i-1只股票且完成j笔交易手上有股票的收益，或者只考虑i-1只股票且完成j笔交易购买当前这只股票收益
sell[i][j] = max(sell[i-1][j], buy[i-1][j-1]+prices[i])
取只考虑i-1只股票且完成j笔交易手上没有股票的收益，或者只考虑i-1只股票且此时卖出股票收益达到j笔交易的收益
这题好绕啊，建议自己码一下，会清晰很多。
代码：
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n = prices.size();
vector<vector<int>> buy(n,vector<int>(k+1,INT_MIN/2));
vector<vector<int>> sell(n,vector<int>(k+1,INT_MIN/2));
if(2*k>=n) k = n/2;
buy[0][0] = -prices[0];
sell[0][0] = 0;
for(int i=1;i<n;i++){
sell[i][0] = 0;
buy[i][0] = max(buy[i-1][0], sell[i-1][0]-prices[i]);
for(int j=1;j<=k;j++){
buy[i][j] = max(buy[i-1][j], sell[i-1][j]-prices[i]);
sell[i][j] = max(sell[i-1][j], buy[i-1][j-1]+prices[i]);
}
}
int res = *(max_element(sell[n-1].begin(), sell[n-1].end()));
return res>=0?res:0;
}
};因为是二维数组，且每次更新只用到[i-1]的值，所以肯定是可以压缩的。
压缩后，因为buy在sell前更新，所以 sell[i][j] = max(sell[i-1][j], buy[i-1][j-1]+prices[i])
就变成了 sell[i][j] = max(sell[i-1][j], buy[i][j-1]+prices[i])
又因为buy[i][j-1] = max(buy[i-1][j-1], sell[i-1][j-1]-prices[i]);
代入 sell[i][j]，得到 sell[i][j] = max(sell[i-1][j], buy[i-1][j-1]+prices[i]，sell[i-1][j-1] -prices[i]+prices[i])
比原本的 sell[i][j]多出了这一项：sell[i-1][j-1] -prices[i]+prices[i]
这一项表示在前i-1只股票中完成了j-1次交易，然后第j次交易是卖入第i只股票再在当天卖出。
所以也是sell[i-1][j]的一种特殊情况，所以多出的这一项不会比sell[i-1][j]大，也就不会影响最终的结果了。
所以是可以压缩数组的。
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
int n = prices.size();
vector<int> buy(k+1,INT_MIN/2);
vector<int> sell(k+1,INT_MIN/2);
if(2*k>=n) k = n/2;
buy[0] = -prices[0];
sell[0] = 0;
for(int i=1;i<n;i++){
buy[0] = max(buy[0], sell[0]-prices[i]);
for(int j=1;j<=k;j++){
buy[j] = max(buy[j], sell[j]-prices[i]);
sell[j] = max(sell[j], buy[j-1]+prices[i]);
}
}
int res = *(max_element(sell.begin(), sell.end()));
return res>=0?res:0;
}
};速度明显变快了：
4）
力扣https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/
股票交易的题，最后代码都不复杂，但是设计转移方程的过程真的很绕。
这题多了一个冷冻期，也就是除了买和卖之外，又多了一个冷冻的状态。
dp[i]表示第i天结束之后的最大收益：
- dp[i][0]表示第i天结束之后，手上持有一只股票
- dp[i][1]表示第i天结束之后，手上不持有股票，且处于冷冻期
- dp[i][1]表示第i天结束之后，手上不持有股票，不处于冷冻期
接下来分类讨论：
dp[i][0]表示第i天结束之后，手上持有一只股票
所以手上这只股票可以是今天买的，也可以是前一天就买了的
dp[i]][0] = max(dp[i-1][2]-prices[i], dp[i-1][0])
dp[i][1]表示第i天结束之后，手上不持有股票，且处于冷冻期
这表示第i天卖了股票，所以第i天结束之后，才会处于冷冻期
dp[i]][0] = dp[i-1][0]+prices[i]
dp[i][1]表示第i天结束之后，手上不持有股票，不处于冷冻期
第i天结束之后不处于冷冻期，那么前一天结束之后可以是冷冻期，也可以不是冷冻期
dp[i]][0] = max(dp[i-1][2], dp[i-1][1])
代码：
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(3,INT_MIN/2));
dp[0][0] = -prices[0];
dp[0][1] = 0;
dp[0][2] = 0;
for(int i=1;i<n;i++){
dp[i][0] = max(dp[i-1][0], dp[i-1][2]-prices[i]);
dp[i][1] = dp[i-1][0]+prices[i];
dp[i][2] = max(dp[i-1][2], dp[i-1][1]);
}
return max(dp[n-1][1], dp[n-1][2]);
}
};转移方程中dp[i]只与dp[i-1]相关，所以可以压缩转移方程。简单地用六个变量来代替二维数组。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(3,INT_MIN/2));
int f0,f1,f2,f3,f4,f5;
f0 = -prices[0];
f1 = 0;
f2 = 0;
for(int i=1;i<n;i++){
f3 = max(f0, f2-prices[i]);
f4 = f0+prices[i];
f5 = max(f2, f1);
f0 = f3;
f1 = f4;
f2 = f5;
}
return max(f1,f2);
}
};速度快了很多：
