DAY45：动态规划（五）背包问题：01背包理论基础+二维DP解决01背包问题

文章目录

- 背包问题大纲
- 01背包
- 01背包暴力解法
- 01背包二维DP解法
- - 二维DP数组的解法
  - - DP数组含义
    - 递推公式
    - 初始化二维DP数组（比较重要）
    - 遍历顺序（比较重要）
  - 二维DP数组完整版
  - - 思路总结
    - 返回值为什么是二维数组最后一个元素
    - DP推导过程与数组含义进一步理解
    - 递推公式理解

对于面试的话，掌握01背包，和完全背包，就够用了，最多可以再来一个多重背包。

背包问题大纲

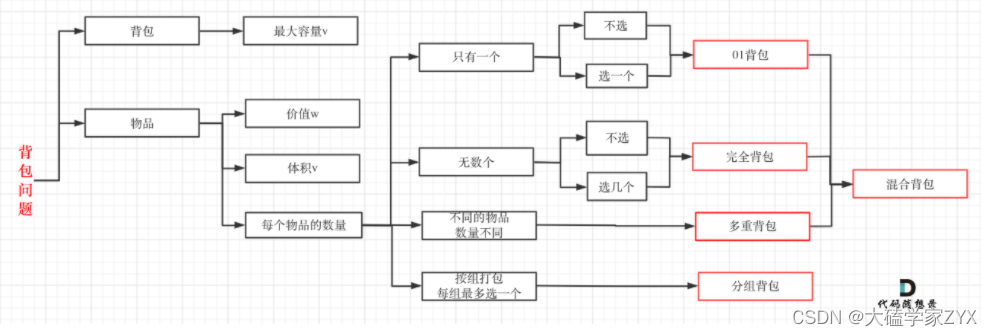
在这里插入图片描述
leetcode上连多重背包的题目都没有，所以题库也告诉我们，01背包和完全背包就够用了。

而完全背包又是也是01背包稍作变化而来，即：完全背包的物品数量是无限的。

所以背包问题的理论基础重中之重是01背包。

leetcode上没有纯背包题目，都是用背包问题的思想去解决和应用，也就是需要转化为01背包问题。

01背包

01背包是有N种物品，每种物品只有一个。完全背包是有N种物品，每种物品有无限个。

多重背包是有N种物品，每种物品个数各不相同。

这几类问题主要体现在物品个数不同。

纯粹的01背包问题如下所示：

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

在这里插入图片描述

01背包暴力解法

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是 O(2^n)，这里的n表示物品数量。

暴力的解法是指数级别的时间复杂度。所以才需要动态规划的解法来进行优化。

#include<bits/stdc++.h>
using namespace std;

struct Item {
    int weight;
    int value;
};

int maxValue = 0;
Item items[3] = {{1, 15}, {3, 20}, {4, 30}};
int n = 3;
int capacity = 4;

void backtrack(int i, int totalWeight, int totalValue) {
    if (i == n || totalWeight == capacity) {
        if (totalValue > maxValue) maxValue = totalValue;
        return;
    }
    backtrack(i + 1, totalWeight, totalValue);
    if (totalWeight + items[i].weight <= capacity)
        backtrack(i + 1, totalWeight + items[i].weight, totalValue + items[i].value);
}

int main() {
    backtrack(0, 0, 0);
    cout << "最大价值是：" << maxValue << endl;
    return 0;
}

backtrack 函数尝试包括或不包括当前位置的物品，如果包括，那么将它的价值和重量加到总价值和总重量中。在每次选择后，程序递归到下一个物品。如果到达物品列表的末尾，或者已经达到背包的最大容量，该函数会检查是否找到了更高的价值，并更新全局最大值（maxValue）。

01背包二维DP解法

二维DP数组的解法

我们先用二维数组的方式去求解。

DP数组含义

我们先定义一个二维DP数组dp。dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

递推公式

确定递推公式的时候，我们要确定dp[i][j]可以由哪几个方向推出来。当前背包的状态就取决于是不是放入物品i。放入物品i是一个状态，不放物品i又是另一个状态。

如果不放物品i，背包容量为j，那么背包当前的最大价值为：dp[i-1][j]，也就是背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以背包内的价值依然和前面相同。)
放物品i，那么放物品i的最大价值，就是背包容量-物品i的容量所能放的最大价值+物品i的价值：dp[i-1][j-weight[i]]+value[i]

放物品i和不放物品i的两个值，取最大值，就是dp[i][j]对应的遍历到i情况下的最大价值。

//递推公式
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);

初始化二维DP数组（比较重要）

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱。

首先由递推公式可以看出，dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i])，因此为了避免数组下标越界，必须满足i>=1，i=0的情况需要单独分析；也就是dp[0][j]需要进行初始化。

同时j-weight[i]因为是不固定数值，因此for循环里单独写if(j<=weight[i]) dp[i][j]=dp[i-1][j]即可。从这个角度出发，我们为了让dp[i][j]=dp[i-1][j]这个式子成立，也需要对dp[0][j]进行初始化。

关于dp[i][0]是否需要初始化的问题，实际上因为j会对if(j<weight[i])单独做判断，因此没有必要初始化dp[i][0]，j从0开始是完全可以的。

DP数组情况如下图所示。

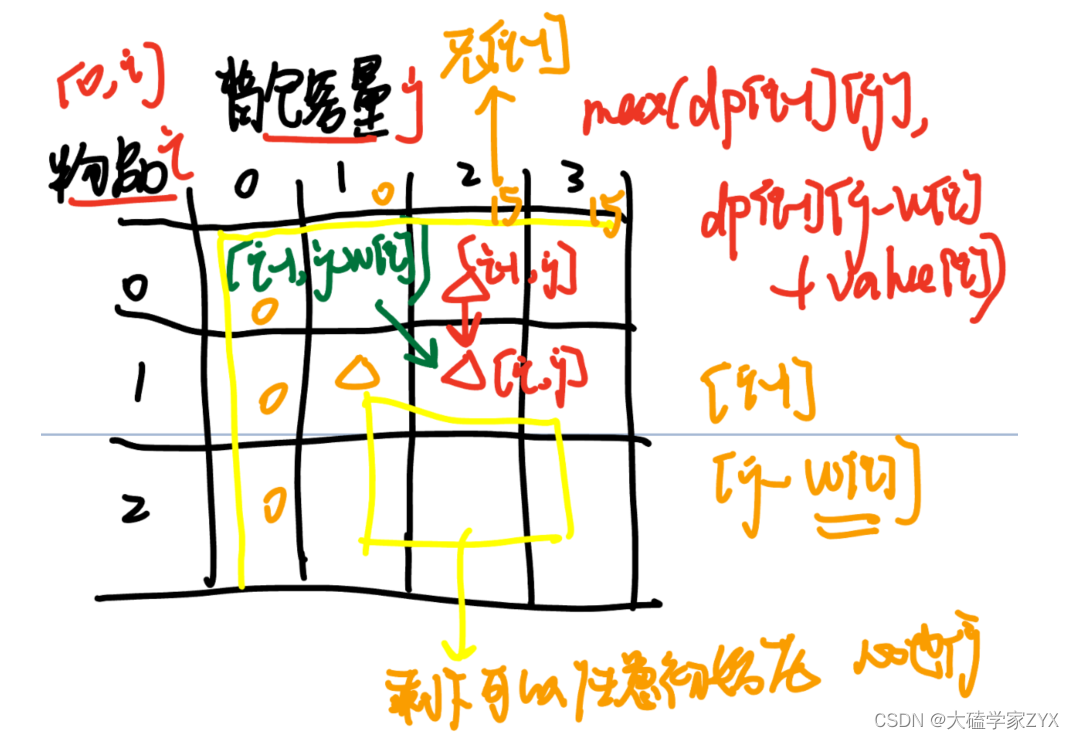
在这里插入图片描述

初始化的时候注意dp数组的定义，dp数组定义是第i个东西放进背包时，背包的最大价值为dp[i]，因此当物品i为0的时候，初始化第一行dp[0][j]就要看物品0放进去的时候，背包有多少价值。
同理，初始化第一列的时候，也是看背包容量为0的时候，对应价值是多少（全是0）
实际上只初始化i=0就可以了，j=0不需要初始化因为遍历会单独写条件

vector<vector<int>>dp(n+1,vector<int>(n+1,0));//全部初始化为0
for(int j=0;j<=bagweight;j++){
    if(j<weight[0]) dp[0][j] = 0;//如果背包容量小于放入物品0的weight，dp[i][j]=0
    else
        dp[0][j]=value[0];
}

遍历顺序（比较重要）

背包类的题目要有两层for循环。一个for遍历物品i，另一个遍历背包容量j。

实际上，对于二维DP数组实现的01背包，这两层for循环的内外嵌套是可以颠倒的。也就是说先遍历物品/背包都是可以的。

我们重新观察这个DP数组，可以发现，因为遍历到i的时候，要么dp取值是放入i，要么是不放入i。因此i的状态是由i上方的元素和左上方的元素决定的。（图中红色三角和绿色三角）

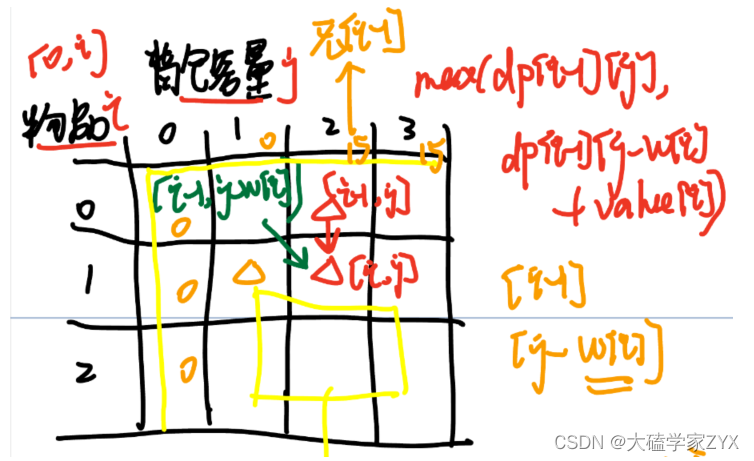
在这里插入图片描述
也就是说，我们遍历到i的时候，需要保证i的左上方和正上方都有数值。因此我们把两个先后顺序进行举例，如下图：（橙色三角是已经初始化的部分）

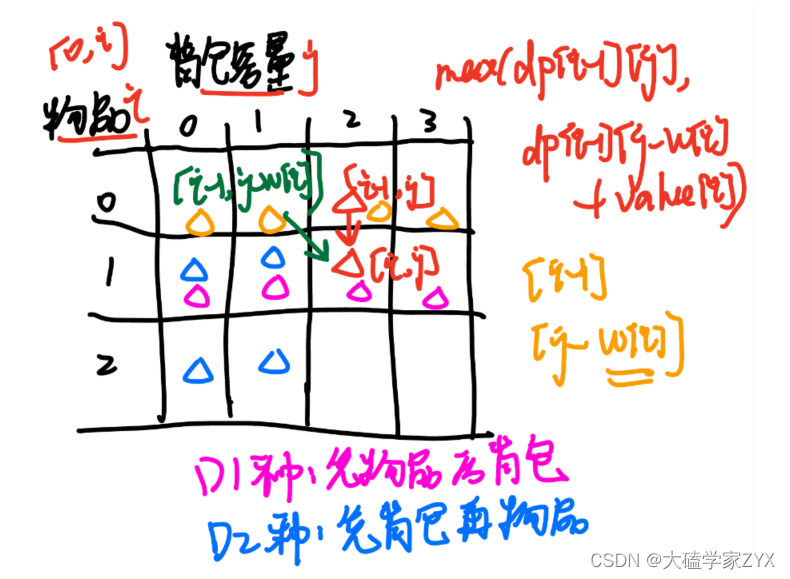
在这里插入图片描述
可以看出，无论是先遍历背包还是先遍历物品，都能保证当前遍历元素的左上方和正上方都有数值。因此两种遍历方式都可以。

二维DP数组完整版

背包最大重量为4。

物品重量和价值为：

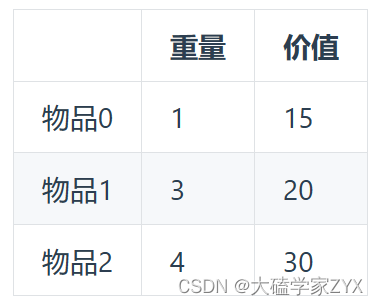
在这里插入图片描述
问背包能背的物品最大价值是多少？

递推公式思想同样是，对于每一个背包大小，都计算出当前背包大小能存放物品的最大价值，那么遍历到指定背包大小的时候，也是最大价值。DP递推公式对于每一个背包数值都适用。
递推公式的大小比较，是已经装了上个物品的状态，和能够装下当前物品，并且已经装了当前物品的状态比较。因此if(j<weight[i])这个判断只是在看当前的背包容量能不能给新来的物品腾地方，只要j>=weight[i]+1，就说明能给当前物品腾出位置。

#include <bits/stdc++.h>
using namespace std;

//传入的是背包容量与物品重量和价值
int knapsack(vector<int>& weight, vector<int>& value, int bagWeight) {
    int n = weight.size();//获取物品数量
    //创建i*j二维数组，i是物品，j是背包容量
    vector<vector<int>>dp(n+1,vector<int>(bagWeight+1,0));
    //二维数组初始化
    for(int j=0;j<=bagWeight;j++){
        if(j<weight[0]) continue; //保持0的数值
        else
            dp[0][j] = value[0];//第一行物品0的情况，也就是i=0那一行的情况
    }
    //遍历物品和背包
    for(int i=1;i<n;i++){
        for(int j=0;j<=bagWeight;j++){
            //看看当前的背包容量能不能给新来的物品腾地方，只要j>=weight[i]+1，就说明能给当前物品腾出位置，当前物品不是在和装了上个物品的状态比较，而是在和没有当前物品的状态比较
            if(j<weight[i]) dp[i][j]=dp[i-1][j];/
            else{
                //放这个i和不放这个i的情况对比，选最大的
                dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
            }
        }
    }
    return dp[n-1][bagWeight];
}

void test_knapsack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;

    cout << knapsack(weight, value, bagWeight) << endl;
}

int main() {
    test_knapsack();
}

思路总结

对于每一种物品（纵轴上的索引i），对于每一个背包大小（横轴上的索引j），都计算出当前背包大小能存放物品的最大价值。如果当前背包的容量无法装下物品i，那么dp[i][j]的值就等于dp[i-1][j]，否则，需要在“不放入物品i”和“放入物品i”这两种选择中选取价值最大的，即max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i])。

这样，遍历到指定背包大小的时候，得到的就是当前背包可以装下物品的最大价值。所以说，这个DP递推公式对于每一个背包数值都适用。

我们需要时刻注意，遍历到每一个物品的时候，dp[i][j]表示的都是：在考虑前i个物品，并且背包容量为j的情况下，背包可以装下的最大价值。

返回值为什么是二维数组最后一个元素

到了最后，就是考虑第[0–n]个物品，背包为j的时候，可以装下的最大价值。因此最后的结果，就是二维数组的最后一个元素。（考虑到了最后一个物品）。这也是DP数组含义相关的问题。

DP推导过程与数组含义进一步理解

当我们不清楚返回值or不清楚递推逻辑的时候，一定要先回去看DP数组与其关联下标的含义。

本题中，DP数组的含义就是，考虑第[0–i]个物品，背包容量为j的情况下，dp[i][j]代表的就是当前背包的最大价值。

物品个数为3，容量为4，对应value是表格中的情况，DP数组预期如下：

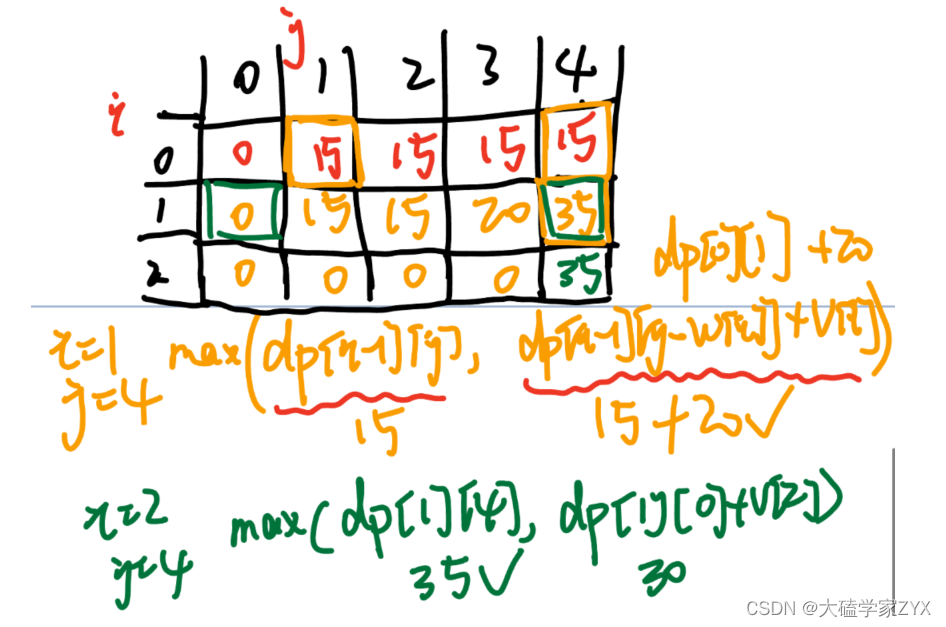
在这里插入图片描述
在动态规划的过程中，对于每一个背包的大小（j）和每一个物品（i），我们需要决定是否将物品i放入背包。这里的决策基于两种情况的比较：

不放入物品i：这种情况下，背包的价值等于没有考虑物品i时，只考虑前i-1个物品，背包容量为j时候，背包的最大价值，即dp[i-1][j]。（看DP数组的定义）
放入物品i：这种情况下，只有当背包的容量j大于等于物品i的重量weight[i]时，才能将物品i放入背包。放入物品i后，背包的价值等于考虑前i-1个物品，且背包剩余容量j-weight[i]时的最大价值加上物品i的价值，也就是dp[i-1][j-weight[i]]+value[i]。（也是通过DP数组含义推算得到）

递推公式理解

只要 j >= weight[i] ，就说明背包的容量足以容纳当前的物品。

if (j < weight[i]) 这个判断在检查当前背包的容量是否足以装下当前考虑的物品。如果背包的容量不足以装下当前的物品，那么 dp[i][j] 的值就应当等于没有装入当前物品，背包容量为j，且只装入前 i - 1 个物品时的最大价值，即 dp[i - 1][j]。

如果 j >= weight[i]，说明背包的容量足以装下当前的物品。此时，我们需要在两种选择之间取最优：一种是选择不装入当前的物品，背包的总价值即为 dp[i - 1][j]；另一种是选择装入当前的物品，然后在剩余的背包容量中尽可能装入更多价值的物品，此时的背包总价值即为 dp[i - 1][j - weight[i]] + value[i]。dp[i][j] 即为这两种选择中的最大值，这就是动态规划的状态转移方程。