【聚类算法】密度峰值聚类算法DPC（Density Peak Clustering Algorithm）

news2024/11/27 4:07:47

every blog every motto: You can do more than you think.
https://blog.csdn.net/weixin_39190382?type=blog

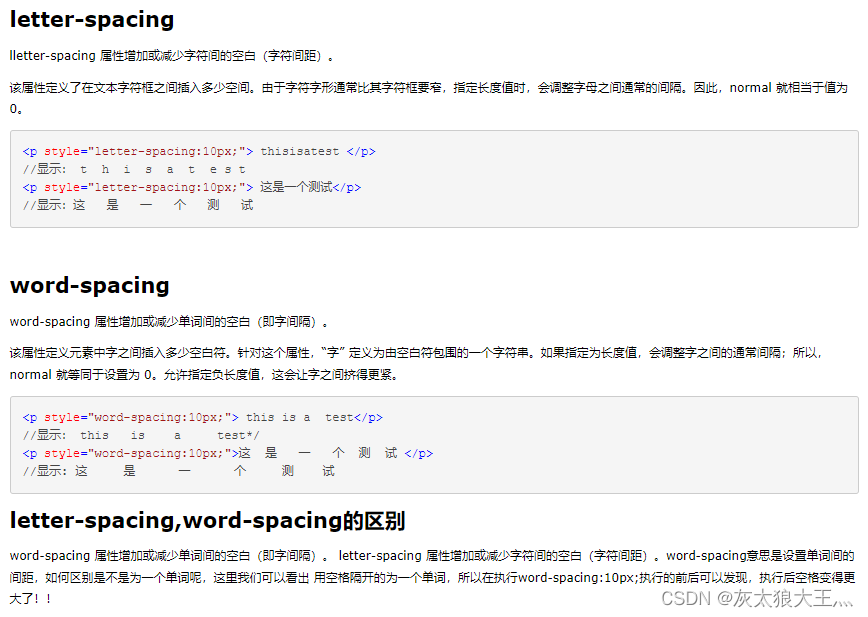
0. 前言

密度峰值聚类算法（Density Peak Clustering Algorithm），能够自动发现数据中的密度峰值点，并根据峰值点将数据进行聚类，该算法由Alex Rodriguez和Alessandro Laio于2014年提出。发表science
https://www.science.org/doi/10.1126/science.1242072

一直感觉聚类算法上个世纪应该研究差不多了，没想到这么近（2014）还有不错的算法提出，而且发表在science，有点激动，23333

1. 正文

1.0 思想

  • 聚类中心密度应当较大
  • 聚类中心应当离比其密度更大的点较远

1.1 概念

  1. 局部密度 ρ \rho ρ ：样本点一定范围内样本的数量，用来描述该点的密度。
  2. 相对距离 δ \delta δ ： 样本点与比他密度更大点之间的距离，一般采用欧式距离。

1.2 实现说明

我们需要计算所有点的局部密度 ρ \rho ρ和相对距离 δ \delta δ，当这两个值都大时，我们将该点定义为密度峰值（类簇中心），然后将剩余点分配给密度比它高的最近数据点所在的类簇。

1.3 密度和距离的计算

1.3.1 局部密度计算

局部密度表示一个样本点一定范围内样本点的数量，反应该点的密集程度

ρ i = ∑ K ( d i s t ( i , j ) ) \rho_i = \sum K(dist(i,j)) ρi​=∑K(dist(i,j))

其中K是一个核函数。常见的核函数有：

  • 高斯核函数 Gaussian kernel
  • 截断核函数 Truncated kernel
  • Epanechnikov
  1. 截断核函数

ρ i = ∑ i ≠ j χ ( d i j − d c ) \rho_i = \sum_{i \neq j} \chi(d_{ij} - d_c) ρi​=i=j∑​χ(dij​−dc​)
χ ( x ) = { 1 , x   <   0 0 , i x   ≥   0 \chi(x) = \begin{cases} 1, & x \ < \ 0\\ 0, &ix \ \geq \ 0 \end{cases} χ(x)={1,0,​x < 0ix ≥ 0​

对于每个点，以dc为半径，统计其中的点的数目。数据越多说明密度越大

对于大规模数据，截断函数聚类效果较好，
小规模数据，高斯核函数聚类效果较好。

1.3.2 相对距离计算

注意： 这个概念很多博客都说了，后面的博客就继续抄错了，具体可看原论文，原始表述是min，而很多博客都表述很max。

在这里插入图片描述
论文左侧红框：

δ i = min ⁡ j : ρ j > ρ i ( d i j ) \delta_i = \min_{j:\rho_j > \rho_i} (d_{ij}) δi​=j:ρj​>ρi​min​(dij​)

一句话概括： 在一个班级里面找成绩比自己好，但是挨着最近的人，计算自己和他的距离

即，找局部密度比当前点 i i i大，但是距离最近的点，计算 i i i到这个点的距离。

论文右侧红框：

For the point with highest density, we conventionally take δ i = m a x i ( d i j ) \delta_i = max_i(d_{ij}) δi​=maxi​(dij​)

翻译：对于密度最大的点，通常认为 δ i = m a x i ( d i j ) \delta_i = max_i(d_{ij}) δi​=maxi​(dij​)

Note that δ i \delta_i δi​ is much larger than the typical nearest neighbor distance only for points that are local or global maxima in the density.

翻译：注意，只有在密度达到局部最大值或全局最大值时，相对距离 δ i \delta_i δi​才比周围的样本（他的邻居）点大很多。

Thus, cluster centers are recognized as points for which the value of δ i \delta_i δi​ is anomalously large

翻译：因此，聚类中心通常最被认为相对距离较大的点

对于密度最高的点，因为上面的表述需要找比自己密度大的点，但已经是密度最高了，所以自然无法找到比自己密度还大的点。那么对于这个点距离怎么算？

该点计算与距离最远的局部密度最大点的距离。

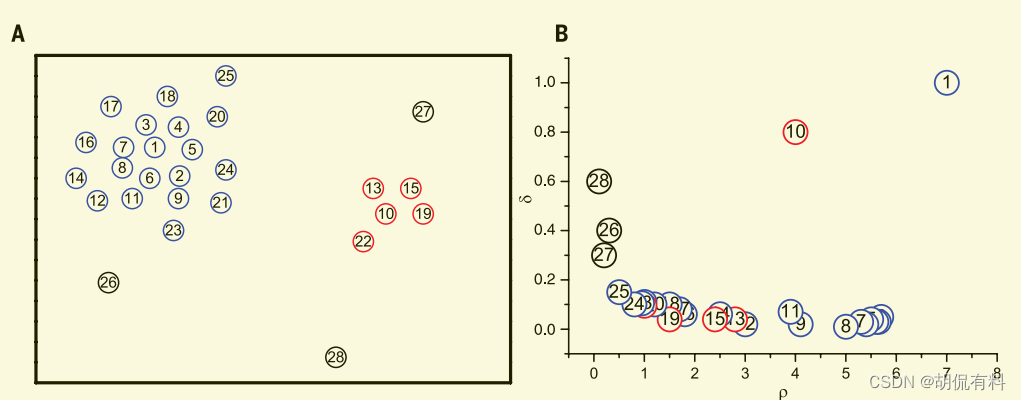
1.3.3 图例说明

右图，

  • 横轴：密度
  • 纵轴：距离

观察：

  • 1和10号点，密度和相对距离都比较大，所以是样本中心
  • 26和28号点密度较低，相对距离较大，所以是异常点
  • 其他点根据和聚类中心的距离，划分到不同的簇中

对于同一簇中的点，非簇中心点，他的相对距离计算时如何的？

他周围的邻居密度可能比大或者簇中心的密度肯定比他大，那么计算他到邻居或者簇中心的距离。因为在同一簇中，这个距离这比较小的。故存在下右图靠近横轴的一排点，密度不同，但相对距离都比较小。
这对应的上面的翻译2。

在这里插入图片描述

1.4 算法步骤

  1. 计算任意两点之间距离
  2. 根据截断距离，计算任意点的局部密度 ρ \rho ρ
  3. 计算任意点的相对距离 δ \delta δ
  4. 以 ρ \rho ρ为横轴， δ \delta δ为纵轴，画出决策树
  5. 利用决策树，将 ρ \rho ρ和 δ \delta δ都大的点标记为簇中心， δ \delta δ大 ρ \rho ρ小的点标记为噪声
  6. 将剩余点进行分配，将每个点分配到它的最近邻且密度比其大的点所在的簇

1.5 案例

import numpy as np
import matplotlib.pyplot as plt
import csv #可以导入csv文件
 
# 计算数据点两两之间的距离
def getDistanceMatrix(datas):
    N, D = np.shape(datas)
    dists = np.zeros([N, N])
 
    for i in range(N):
        for j in range(N):
            vi = datas[i, :]
            vj = datas[j, :]
            dists[i, j] = np.sqrt(np.dot((vi - vj), (vi - vj)))
    return dists
 
 
# 找到密度计算的阈值dc
# 要求平均每个点周围距离小于dc的点的数目占总点数的1%-2%
def select_dc(dists):
    '''算法1'''
    N = np.shape(dists)[0]
    tt = np.reshape(dists, N * N)
    percent = 2.0
    position = int(N * (N - 1) * percent / 100)
    dc = np.sort(tt)[position + N]
    return dc
 
 
# 计算每个点的局部密度
def get_density(dists, dc, method=None):
    N = np.shape(dists)[0]
    rho = np.zeros(N)
 
    for i in range(N):
        if method == None:
            rho[i] = np.where(dists[i, :] < dc)[0].shape[0] - 1
        else:
            rho[i] = np.sum(np.exp(-(dists[i, :] / dc) ** 2)) - 1
    return rho
 
 
# 计算每个数据点的密度距离
# 即对每个点，找到密度比它大的所有点
# 再在这些点中找到距离其最近的点的距离
def get_deltas(dists, rho):
    N = np.shape(dists)[0]
    deltas = np.zeros(N)
    nearest_neiber = np.zeros(N)
    # 将密度从大到小排序
    index_rho = np.argsort(-rho)
    for i, index in enumerate(index_rho):
        # 对于密度最大的点
        if i == 0:
            continue
 
        # 对于其他的点
        # 找到密度比其大的点的序号    
        index_higher_rho = index_rho[:i]
        # 获取这些点距离当前点的距离,并找最小值
        deltas[index] = np.min(dists[index, index_higher_rho])
 
        # 保存最近邻点的编号
        index_nn = np.argmin(dists[index, index_higher_rho])
        nearest_neiber[index] = index_higher_rho[index_nn].astype(int)
 
    deltas[index_rho[0]] = np.max(deltas)
    return deltas, nearest_neiber
 
 
# 通过阈值选取 rho与delta都大的点
# 作为聚类中心    
def find_centers_auto(rho, deltas):
    rho_threshold = (np.min(rho) + np.max(rho)) / 2
    delta_threshold = (np.min(deltas) + np.max(deltas)) / 2
    N = np.shape(rho)[0]
 
    centers = []
    for i in range(N):
        if rho[i] >= rho_threshold and deltas[i] > delta_threshold:
            centers.append(i)
    return np.array(centers)
 
 
# 选取 rho与delta乘积较大的点作为
# 聚类中心   
def find_centers_K(rho, deltas, K):
    rho_delta = rho * deltas
    centers = np.argsort(-rho_delta)
    return centers[:K]
 
 
def cluster_PD(rho, centers, nearest_neiber):
    K = np.shape(centers)[0]
    if K == 0:
        print("can not find centers")
        return
 
    N = np.shape(rho)[0]
    labs = -1 * np.ones(N).astype(int)
 
    # 首先对几个聚类中进行标号
    for i, center in enumerate(centers):
        labs[center] = i
 
    # 将密度从大到小排序
    index_rho = np.argsort(-rho)
    for i, index in enumerate(index_rho):
        # 从密度大的点进行标号
        if labs[index] == -1:
            # 如果没有被标记过
            # 那么聚类标号与距离其最近且密度比其大
            # 的点的标号相同
            labs[index] = labs[int(nearest_neiber[index])]
    return labs
 
 
def draw_decision(rho, deltas, name="0_decision.jpg"):
    plt.cla()
    for i in range(np.shape(datas)[0]):
        plt.scatter(rho[i], deltas[i], s=16., color=(0, 0, 0))
        plt.annotate(str(i), xy=(rho[i], deltas[i]), xytext=(rho[i], deltas[i]))
        plt.xlabel("rho")
        plt.ylabel("deltas")
    plt.savefig(name)
    plt.show()
 
def draw_cluster(datas, labs, centers, dic_colors, name="0_cluster.jpg"):
    plt.cla()
    K = np.shape(centers)[0]
 
    for k in range(K):
        sub_index = np.where(labs == k)
        sub_datas = datas[sub_index]
        # 画数据点
        plt.scatter(sub_datas[:, 0], sub_datas[:, 1], s=16., color=dic_colors[k])
        # 画聚类中心
        plt.scatter(datas[centers[k], 0], datas[centers[k], 1], color="k", marker="+", s=200.)
    plt.savefig(name)
    plt.show()
 
 
if __name__ == "__main__":
    dic_colors = {0: (.8, 0, 0), 1: (0, .8, 0),
                  2: (0, 0, .8), 3: (.8, .8, 0),
                  4: (.8, 0, .8), 5: (0, .8, .8),
                  6: (0, 0, 0)}
    # file_name='spiral'
    # with open('spiral.txt','r') as f:
    #     lines = f.read().splitlines()
    # lines = [line.split("\t")[:-1] for line in lines]
    # datas = np.array(lines).astype(np.float32)
    file_name='iris'
    with open('iris.csv','r') as fc:
        reader=csv.reader(fc)
        lines1=[]
        for line in reader:
            lines1.append(line)
    lines=lines1[1:]
    print("lines:\n", lines)
    datas = np.array(lines).astype(np.float32)
    print("datas:\n", datas)
    # 计算距离矩阵
    dists = getDistanceMatrix(datas)
    # 计算dc
    dc = select_dc(dists)
    print("dc", dc)
    # 计算局部密度 
    rho = get_density(dists, dc, method="Gaussion")
    # 计算密度距离
    deltas, nearest_neiber = get_deltas(dists, rho)
 
    # 绘制密度/距离分布图
    draw_decision(rho, deltas, name=file_name + "_decision.jpg")
 
    # 获取聚类中心点
    centers = find_centers_K(rho, deltas, 3)
    # centers = find_centers_auto(rho,deltas)
    print("centers", centers)
 
    labs = cluster_PD(rho, centers, nearest_neiber)
    draw_cluster(datas, labs, centers, dic_colors, name=file_name + "_cluster.jpg")

1.6 存在的问题

该部分参考：https://www.cnblogs.com/eisenji/p/16417340.html

1.6.1 多密度峰问题

如果可以在一个簇中找到两个具有较高局部密度和相对距离较大的数据点，这两个点就会被识别成两个簇心。比如下左图被聚成了下右图。优化是，改进该算法中“一个簇只有一个密度峰”的假设。比如，很多改进算法是先以各种算法进行预聚类，再通过各种方法拆分聚类结果，再通过各种方法合并拆分的结果；或者是先拆分后合并。

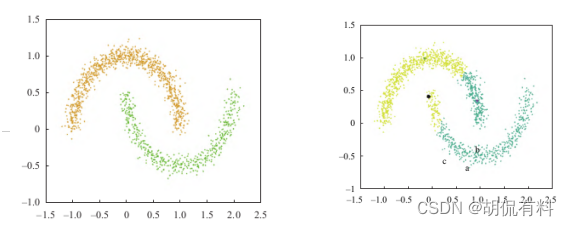
请添加图片描述

1.6.2 分配策略问题

完成簇心的识别后，其余每个点分配到与其最近的高密度点的同一个簇。于是可能会出现下图的错误：a点周围的点的密度都不超过a点。距离a点最近的高密度点是b点，但是a点实际上不应该与b归为一簇，而应该与c点归为同一簇。而分配错了这个点，将导致更多与之相连的点被错误聚类。优化是，边分配边调错；将一步完成分配改为两步或多步；DPC算法只计算了通过点之间关系计算距离和密度，可加入更多的量来协助点的分配。

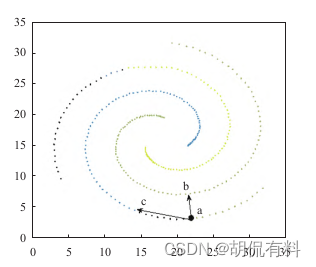
请添加图片描述

1.6.3 复杂度问题

时间空间都是n²复杂度，需要很高计算成本，限制了该算法在大规模数据集上的应用。优化是，比如，用网格对象代替数据对象，减少距离计算。或者，对数据进行预划分，同时除去一些小密度的数据对象；或者通过某些方法判定除去更多的不需要参与计算的数据对象，不过需要保证损失聚类精度在可控的范围内。

参考

[1] https://blog.csdn.net/lijunyan5/article/details/116161915
[2] https://blog.csdn.net/m0_74086448/article/details/131635573
[3] https://zhuanlan.zhihu.com/p/406113860
[4] https://www.cnblogs.com/kailugaji/articles/11379198.html#:~:text=%E5%9F%BA%E4%BA%8E%E5%AF%86%E5%BA%A6%E5%B3%B0%E5%80%BC%E7%9A%84%E8%81%9A%E7%B1%BB%E7%AE%97%E6%B3%95%E5%85%A8%E7%A7%B0%E4%B8%BA%E5%9F%BA%E4%BA%8E%E5%BF%AB%E9%80%9F%E6%90%9C%E7%B4%A2%E5%92%8C%E5%8F%91%E7%8E%B0%E5%AF%86%E5%BA%A6%E5%B3%B0%E5%80%BC%E7%9A%84%E8%81%9A%E7%B1%BB%E7%AE%97%E6%B3%95%20%28clustering%20by%20fast%20search%20and,find%20of%20density%20peaks%2C%20DPC%29%E3%80%82%20%E5%AE%83%E6%98%AF2014%E5%B9%B4%E5%9C%A8Science%E4%B8%8A%E6%8F%90%E5%87%BA%E7%9A%84%E8%81%9A%E7%B1%BB%E7%AE%97%E6%B3%95%EF%BC%8C%E8%AF%A5%E7%AE%97%E6%B3%95%E8%83%BD%E5%A4%9F%E8%87%AA%E5%8A%A8%E5%9C%B0%E5%8F%91%E7%8E%B0%E7%B0%87%E4%B8%AD%E5%BF%83%EF%BC%8C%E5%AE%9E%E7%8E%B0%E4%BB%BB%E6%84%8F%E5%BD%A2%E7%8A%B6%E6%95%B0%E6%8D%AE%E7%9A%84%E9%AB%98%E6%95%88%E8%81%9A%E7%B1%BB%E3%80%82
[5] https://blog.csdn.net/qq_37055672/article/details/130000567
[6] https://sci-hub.hkvisa.net/10.1126/science.1242072
[7] https://blog.csdn.net/weixin_45317919/article/details/121472851
[8] https://www.cnblogs.com/eisenji/p/16417340.html

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/746011.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java：创建文件夹并输出内容到文件中

Java：创建文件夹并输出内容到文件中

前言 在实际开发当中我们往往会遇到需要用 Java 代码来进行在我们项目的部署的服务器上创建一个文件并向里面写入想要的数据&#xff0c;下面就是具体的实现方式&#xff0c;希望对小伙伴们有用。 代码 这里我把这个操作封装成了一个工具类&#xff0c;方便根据不同业务场景…
阅读更多...
中国品牌在海外做独立站有什么优势？

中国品牌在海外做独立站有什么优势？

从人口红利驱动转向消费升级驱动——品牌出海行业的变局正在上演&#xff0c;低价不再是适用于所有出海企业的策略。从产品出海走向真正意义上的品牌出海&#xff0c;正在成为一部分中国商家的选择。 无论是做品牌还是做全球化&#xff0c;都不容易。消费者购买的不止产品&…
阅读更多...
从零开始 verilog 以太网交换机（六）帧处理单元设计与实现

从零开始 verilog 以太网交换机（六）帧处理单元设计与实现

从零开始 verilog 以太网交换机&#xff08;六&#xff09;帧处理单元设计与实现 &#x1f508;声明&#xff1a; &#x1f603;博主主页&#xff1a;王_嘻嘻的CSDN主页 &#x1f9e8; 从零开始 verilog 以太网交换机系列专栏&#xff1a;点击这里 &#x1f511;未经作者允许&a…
阅读更多...
Android Java代码与JNI交互 JNI访问Java构造方法(九)

Android Java代码与JNI交互 JNI访问Java构造方法(九)

🔥 Android Studio 版本 🔥 🔥 创建包含JNI的类 JNIConstructorClass.java 🔥 package com.cmake.ndk1.jni;import com.cmake.ndk1.model.Animal;public class JNIConstructorClass {static {System.loadLibrary("constructor-class-lib");}public native…
阅读更多...
深度学习——CNN卷积神经网络

深度学习——CNN卷积神经网络

基本概念 概述 卷积神经网络&#xff08;Convolutional Neural Network&#xff0c;CNN&#xff09;是一种深度学习中常用于处理具有网格结构数据的神经网络模型。它在计算机视觉领域广泛应用于图像分类、目标检测、图像生成等任务。 核心思想 CNN 的核心思想是通过利用局部…
阅读更多...
环形链表(快慢指针)

环形链表(快慢指针)

给你一个链表的头节点 head &#xff0c;判断链表中是否有环。如果链表中有某个节点&#xff0c;可以通过连续跟踪 next 指针再次到达&#xff0c;则链表中存在环。 为了表示给定链表中的环&#xff0c;评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置&#xff08;索…
阅读更多...
C++ | 继承

C++ | 继承

目录 前言 一、继承的基本概念与使用 1、继承的概念 2、继承的定义 3、继承的访问限定符与继承方式 二、基类与派生类之间的赋值转换&#xff08;切片&#xff09; 三、继承中的作用域 1、继承中的作用域 2、隐藏&#xff08;重定义&#xff09; 四、派生类的默认构…
阅读更多...
知识付费小程序怎么做

知识付费小程序怎么做

知识付费小程序是一种通过在线平台提供知识和教育内容的应用程序。下面将详细介绍其功能&#xff1a; 1. 音频视频课程&#xff1a; 知识付费小程序提供了丰富的音频和视频课程&#xff0c;在这些课程中&#xff0c;用户可以通过观看或听取专业讲师的讲解来学习各种知识领域。…
阅读更多...
【文章系列解读】Nerf

【文章系列解读】Nerf

1. Nerf NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis 2020年8月3日 &#xff08;0&#xff09;总结 NeRF工作的过程可以分成两部分&#xff1a;三维重建和渲染。&#xff08;1&#xff09;三维重建部分本质上是一个2D到3D的建模过程&#xff…
阅读更多...
Java习题之实现平方根(sqrt)函数

Java习题之实现平方根(sqrt)函数

目录 前言 二分查找 牛顿迭代法 总结 &#x1f381;博主介绍&#xff1a;博客名为tq02&#xff0c;已学C语言、JavaSE&#xff0c;目前学了MySQL和JavaWed &#x1f3a5;学习专栏&#xff1a; C语言 JavaSE MySQL基础 &#x1f384;博主链接&#xff1a;tq02的…
阅读更多...
【第四章 flutter-初识flutter】

【第四章 flutter-初识flutter】

文章目录 一、目录结构二、创建一个flutter项目三、创建自定义组件四、Container组件 就是divalignment 内容对齐方式decoration 类似border 为BoxDecoration的类 五、Text属性六、image组件总结、 一、目录结构 android、ios各自平台的资源文件 lib 项目目录 linux macos PC平…
阅读更多...
Linux宝塔Mysql读写分离配置，两台服务器，服务器存在多个库

Linux宝塔Mysql读写分离配置，两台服务器，服务器存在多个库

Linux宝塔Mysql读写分离配置&#xff0c;两台服务器&#xff0c;服务器存在多个库 一、主库操作 #登录数据库&#xff0c;用root登录方便&#xff0c;用其他账号会提示权限不足&#xff0c;需要登录root给予权限 mysql -u root -p 密码#创建一个账号&#xff0c;供从库用该账…
阅读更多...
电商企业需要部署WMS仓储管理系统吗

电商企业需要部署WMS仓储管理系统吗

随着电子商务行业的迅速发展&#xff0c;电商企业面临着日益增长的订单量和复杂的物流流程。为了提高仓储管理的效率和准确性&#xff0c;许多电商企业开始考虑部署WMS仓储管理系统。然而&#xff0c;是否真的需要部署WMS仓储管理系统&#xff0c;仍然是一个值得探讨的问题。本…
阅读更多...
vLLM大模型推理加速方案原理（PagedAttention）

vLLM大模型推理加速方案原理（PagedAttention）

一、vLLM 简介 vLLM 用于大模型并行推理加速&#xff0c;核心是 PagedAttention 算法&#xff0c;官网为&#xff1a;https://vllm.ai/。 vLLM 主要特性&#xff1a; 先进的服务吞吐量通过 PagedAttention 对注意力 key 和 value 进行内存管理对传入请求的批处理针对 CUDA 内…
阅读更多...
纯代码和低代码的本质区别

纯代码和低代码的本质区别

一、前言 纯代码和低代码是现代软件开发中两种不同的方法。 纯代码需要专业的编程技能&#xff0c;掌握编程语言、算法和数据结构等专业知识。而低代码则是一种新兴的开发方法&#xff0c;它大大降低了对编程技能的要求&#xff0c;让非技术人员也能够创建应用程序。随着低代码…
阅读更多...
【SpringBoot】--03.数据访问、基础特性(外部化和内部外配置、整合JUnit)

【SpringBoot】--03.数据访问、基础特性(外部化和内部外配置、整合JUnit)

文章目录 SpringBoot3-数据访问1.整合SSM场景1.1创建SSM整合项目1.2配置数据源1.3配置MyBatis1.4CRUD编写 2.自动配置原理3.扩展&#xff1a;整合其他数据源3.1 Druid 数据源 SpringBoot3-基础特性1. SpringApplication1.1 自定义 banner1.2.自定义 SpringApplication1.3Fluent…
阅读更多...
nvm 管理node 环境配置

nvm 管理node 环境配置

nvm安装&#xff1a; nvm&#xff08;Node Version Manager&#xff09;是一个用来管理node版本的工具。我们之所以需要使用node&#xff0c;是因为我们需要使用node中的npm(Node Package Manager)&#xff0c;使用npm的目的是为了能够方便的管理一些前端开发的包&#xff01;…
阅读更多...
ColorOS凭什么夺冠？

ColorOS凭什么夺冠？

摘要&#xff1a;五大主流安卓系统流畅度PK&#xff0c;谁的体验最好&#xff1f; 评价一款手机&#xff0c;你最先看的是什么&#xff1f; 是处理器平台&#xff1f;CPU核心频率&#xff1f;还是内存配置&#xff1f; 虽然这些硬件参数能够清晰地反映几款不同配置手机之间的性…
阅读更多...
20230712-----阻塞IO驱动按键控制LED灯的亮灭

20230712-----阻塞IO驱动按键控制LED灯的亮灭

驱动程序 #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/device.h> #include <linux/cdev.h> #include <linux/slab.h> #include <linux/uaccess.h> #include <linux/of.h> #in…
阅读更多...
TeeChart for.NET Crack

TeeChart for.NET Crack

TeeChart for.NET Crack TeeChart for.NET为各种图表需求提供了图表控件&#xff0c;包括金融、科学和统计等重要的垂直领域。它可以处理您的数据&#xff0c;在各种平台上无缝创建信息丰富、引人入胜的图表&#xff0c;包括Windows窗体、WPF、带有HTML5/Javascript渲染的ASP.N…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023