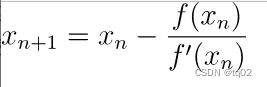Java习题之实现平方根(sqrt)函数

news2024/12/23 20:31:53

前言

二分查找

牛顿迭代法

总结

🎁博主介绍：博客名为tq02，已学C语言、JavaSE，目前学了MySQL和JavaWed

🎥学习专栏： C语言 JavaSE MySQL基础

🎄博主链接：tq02的博客_CSDN博客-C语言,Java,MySQL领域博主

前言

可使用java.lang.Math类的sqrt(double)方法求平方根。Math是java.lang包中的类，而Double为对象中的基本类型。但是如果不使用库函数呢？有什么办法实现平方根函数呢？

方法：二分查找、牛顿迭代法、利用平方数的性质

利用平方数的性质

平方数的性质：n²=1+1+2+2+....+n-1+n-1+n。例如4²=1+1+2+2+3+3+4=16。

1+3为2的平方，1+3+5为3的平方，

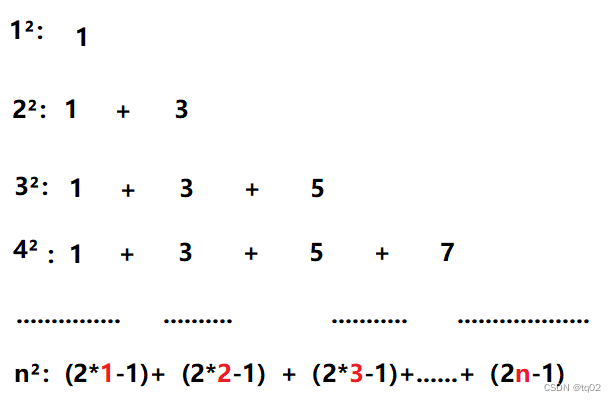
也就是说每一次加一个奇数，再设置一个变量记录加了多少个奇数。

复杂度分析：
时间复杂度：O(N)，每次+2的循环，为(1/2)N的时间复杂度,去掉系数，为O(N)
空间复杂度: O(1),只使用了有限常数个变量；

int sqrt(int x) {
     if(x<=0) return 0;  //小于等于0 返回0
     int ans = 1; 
     int num = 1;
     int  i = 3;
     while(num+i<=x){
         num+=i;  
          ans ++; // 每加一个奇数，ans+1
          i += 2;
        }
        return ans;
    }

二分查找

如果求解一个数的平方根，这个结果肯定是在1到这个数的范围，因此我们可以使用二分查找的方法。例如求解x的平方根，思路：

初始范围：1 ~ x，使用left标记1，right标记x ，取left~right的中间值，为 middle；
当middle*middle <= x && (middle+1)*(middle+1) > x时，返回结果
当 middle*middle < x时，到右半部分继续寻找，范围改成 middle+1 ~ right
当middle*middle > x时，到左半部分继续寻找，范围改成 left ~ middle+1

注：这种方法只能使用于整数的开跟

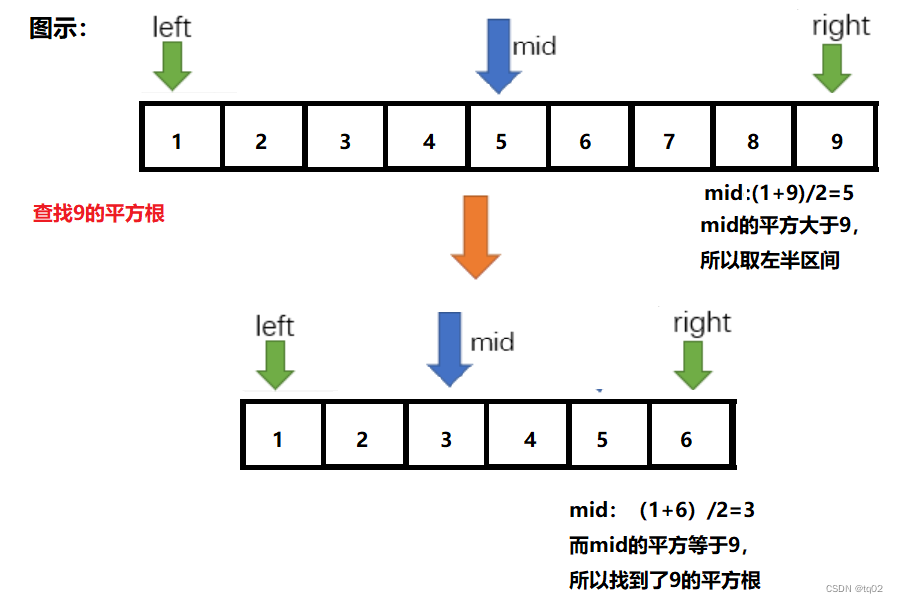
复杂度分析：
时间复杂度:O(logn),二分查找的复杂度，每次循环减少一半
空间复杂度;O(1)，只使用了有限常数个变量；

代码实现：

public int mySqrt(int x) {
    if (x <= 0) {
        return 0;
    }
    int left = 1, right = x;
    while (true) {
        int middle = (left + right) >> 1;
        if (middle <= x / middle && (middle+1) > x / (middle+1)) {
            return (int) middle;
        } else if (middle < x / middle) {
            left = middle + 1;
        } else {
            right = middle - 1;
        }
    }
}

牛顿迭代法

牛顿迭代法简介

假设方程 F(x)=0 在 x 附近有一个根，那么用以下迭代式子：

依次计算X1、X2、X3、...........那么序列将无限逼近方程的根。

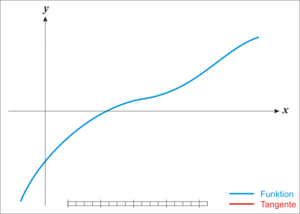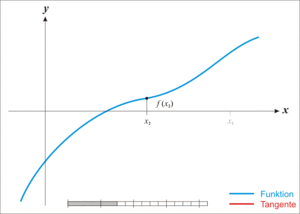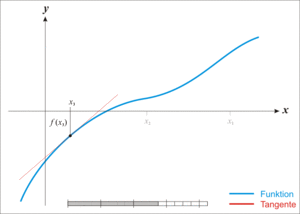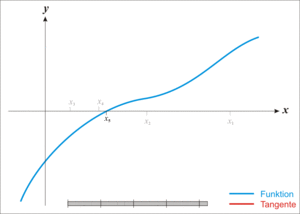
牛顿迭代法的原理很简单，其实是根据f(x)在x0附近的值和斜率，估计f(x)和x轴的交点，看下面的动态图：

代码示例：

public class Solution {
	public int sqrt (int x) {//牛顿迭代法
        if(x==0||x==1) return x;//题中告诉我们x的范围： 0 <= x < 2^31-1
		long X0 = x;//使用int进行加法运算可能溢出，所以采用long型
		long X1 = 0;//下一个迭代变量，为了方便理解，也可只使用X0
		while(X0 > x/X0 ) {    // X0^2>x循环
			X1=(X0+x/X0) >> 1;//由迭代公式得，采用右移1位操作代替除以2，运算更快
			X0=X1;//把下一个迭代变量赋给X0,统一操作，方便继续处理
		}
		return (int)X0;//返回值类型为int,因此需要做强制类型转换
    }
}