卷积神经网络(CNN)

PS： 卷积神经网络 主要包括：输入层、卷积层、池化层、全连接层

1. 卷积神经网络结构介绍

如果用全连接神经网络处理大尺寸图像具有三个明显的缺点：

（1）首先将图像展开为向量会丢失空间信息；

（2）其次参数过多效率低下，训练困难；

（3）同时大量的参数也很快会导致网络过拟合。

而使用卷积神经网络可以很好地解决上面的三个问题。

​ 与常规神经网络不同，卷积神经网络的各层中的神经元是3维排列的：宽度、高度和深度。其中的宽度和高度是很好理解的，因为本身卷积就是一个二维模板。深度：比如 32x32x3（宽度，高度和深度）中 *3 就是（RGB）图片形式 分为三层（代表了红、绿、蓝3种颜色通道）三层颜色拼在一起

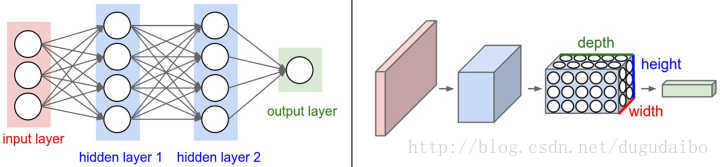
​ 图 1. **全连接神经网络（左） ** 与 **卷积神经网络（右）**的对比

• 全连接神经网络（左）：

​ 输入的是一维的， 32 * 32 *3 = 3072 个一维的像素点

• 卷积神经网络（右）：

​ 输入的是一个三维的 :32 * 32 * 3 直接输入

2、CNN解决了什么问题

在 CNN 出现之前，图像对于人工智能来说是一个难题，有2个原因：

1. 图像需要处理的数据量太大，导致成本很高，效率很低
2. 图像在数字化的过程中很难保留原有的特征，导致图像处理的准确率不高

下面就详细说明一下这2个问题：

2.1、需要处理的数据量太大

图像是由像素构成的，每个像素又是由颜色构成的。

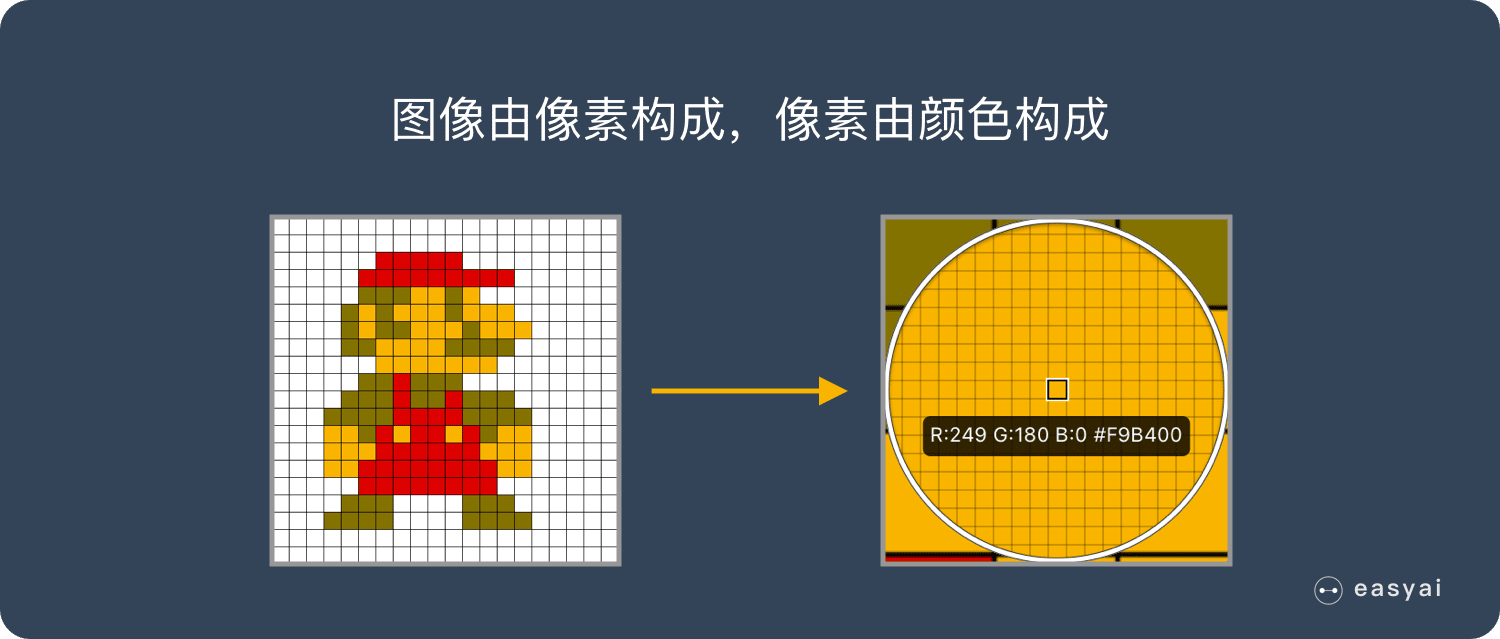
现在随随便便一张图片都是 1000×1000 像素以上的， 每个像素都有RGB 3个参数来表示颜色信息。

假如我们处理一张 1000×1000 像素的图片，我们就需要处理3百万个参数！

1000×1000×3=3,000,000

这么大量的数据处理起来是非常消耗资源的，而且这只是一张不算太大的图片！

卷积神经网络 – CNN 解决的第一个问题就是“将复杂问题简化”，把大量参数降维成少量参数，再做处理。

更重要的是：我们在大部分场景下，降维并不会影响结果。比如1000像素的图片缩小成200像素，并不影响肉眼认出来图片中是一只猫还是一只狗，机器也是如此。

2.2、保留图像特征

图片数字化的传统方式我们简化一下，就类似下图的过程：

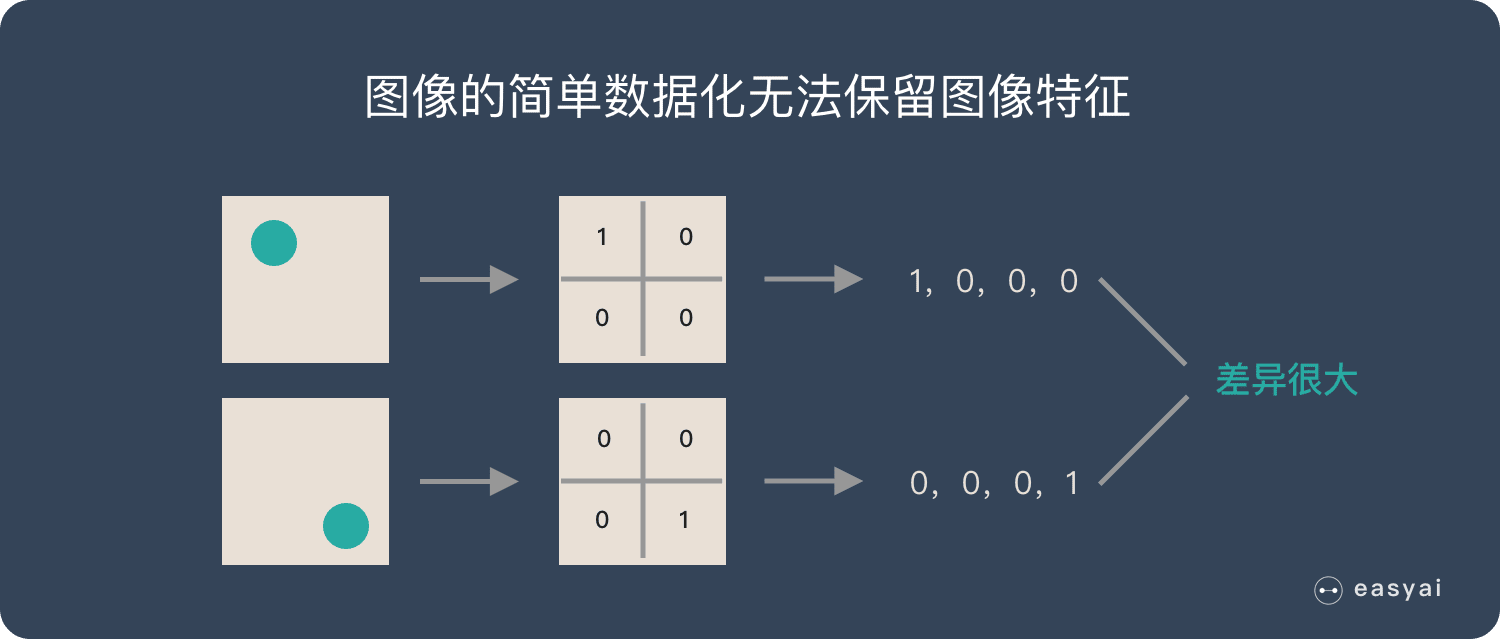
假如有圆形是1，没有圆形是0，那么圆形的位置不同就会产生完全不同的数据表达。但是从视觉的角度来看，图像的内容（本质）并没有发生变化，只是位置发生了变化。

所以当我们移动图像中的物体，用传统的方式的得出来的参数会差异很大！这是不符合图像处理的要求的。

而 CNN 解决了这个问题，他用类似视觉的方式保留了图像的特征，当图像做翻转，旋转或者变换位置时，它也能有效的识别出来是类似的图像。

那么卷积神经网络是如何实现的呢？在我们了解 CNN 原理之前，先来看看人类的视觉原理是什么？

3、人类的视觉原理

深度学习的许多研究成果，离不开对大脑认知原理的研究，尤其是视觉原理的研究。

1981 年的诺贝尔医学奖，颁发给了 David Hubel（出生于加拿大的美国神经生物学家） 和TorstenWiesel，以及 Roger Sperry。前两位的主要贡献，是“发现了视觉系统的信息处理”，可视皮层是分级的。

人类的视觉原理如下：从原始信号摄入开始（瞳孔摄入像素 Pixels），接着做初步处理（大脑皮层某些细胞发现边缘和方向），然后抽象（大脑判定，眼前的物体的形状，是圆形的），然后进一步抽象（大脑进一步判定该物体是只气球）。下面是人脑进行人脸识别的一个示例：

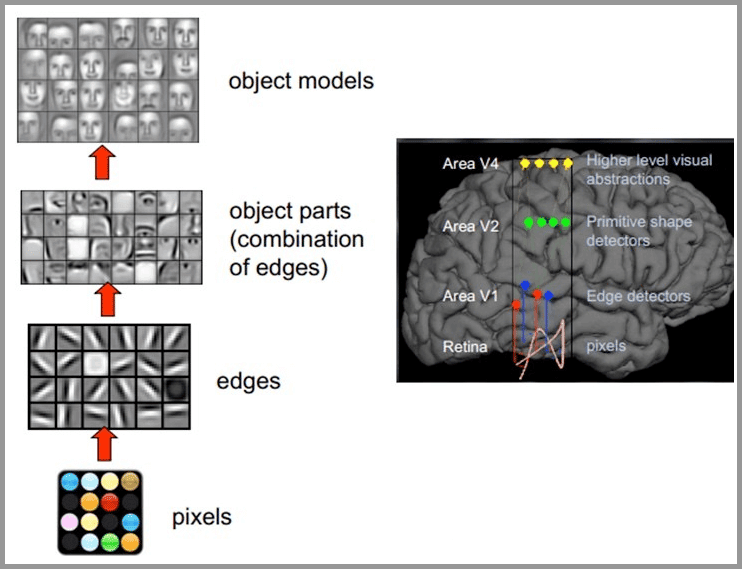
对于不同的物体，人类视觉也是通过这样逐层分级，来进行认知的：

我们可以看到，在最底层特征基本上是类似的，就是各种边缘，越往上，越能提取出此类物体的一些特征（轮子、眼睛、躯干等），到最上层，不同的高级特征最终组合成相应的图像，从而能够让人类准确的区分不同的物体。

那么我们可以很自然的想到：可以不可以模仿人类大脑的这个特点，构造多层的神经网络，较低层的识别初级的图像特征，若干底层特征组成更上一层特征，最终通过多个层级的组合，最终在顶层做出分类呢？

答案是肯定的，这也是许多深度学习算法（包括CNN）的灵感来源。

4、卷积神经网络-CNN 的基本原理

典型的 CNN 由3个部分构成：

1. 卷积层
2. 池化层
3. 全连接层

如果简单来描述的话：

卷积层负责提取图像中的局部特征；池化层用来大幅降低参数量级(降维)；全连接层类似传统神经网络的部分，用来输出想要的结果。

4.1 卷积层——提取特征

卷积层涉及到参数：

• 滑动窗口的步长
• 卷积核尺寸
• 边缘填充
• 卷积核个数

4.4.1 得到的特征图的表示

卷积层的运算过程如下图，用一个卷积核扫完整张图片：

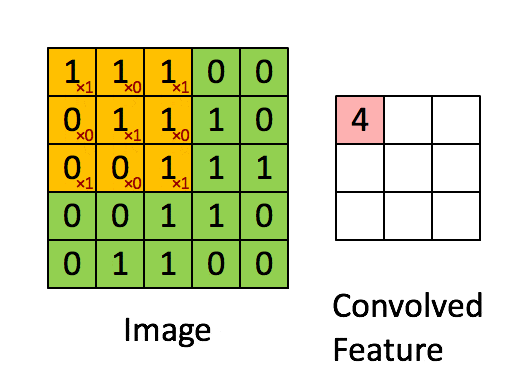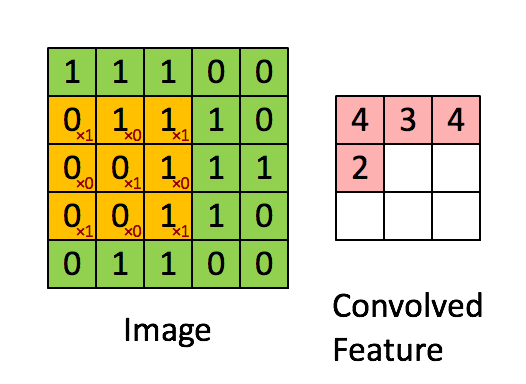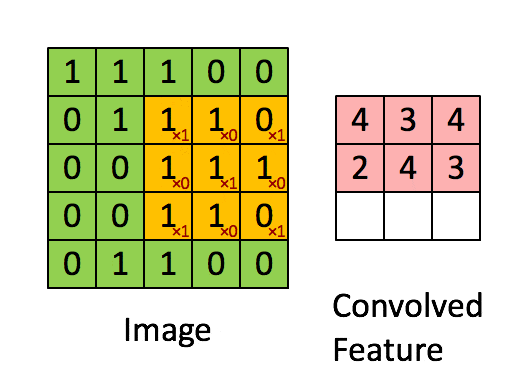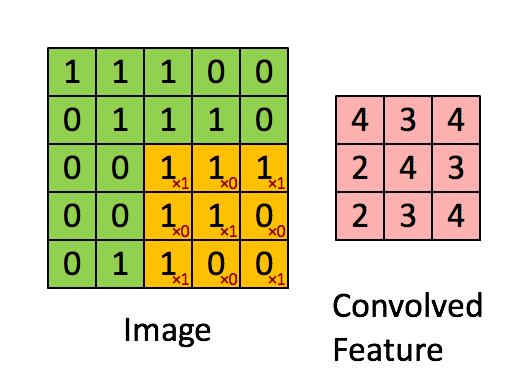
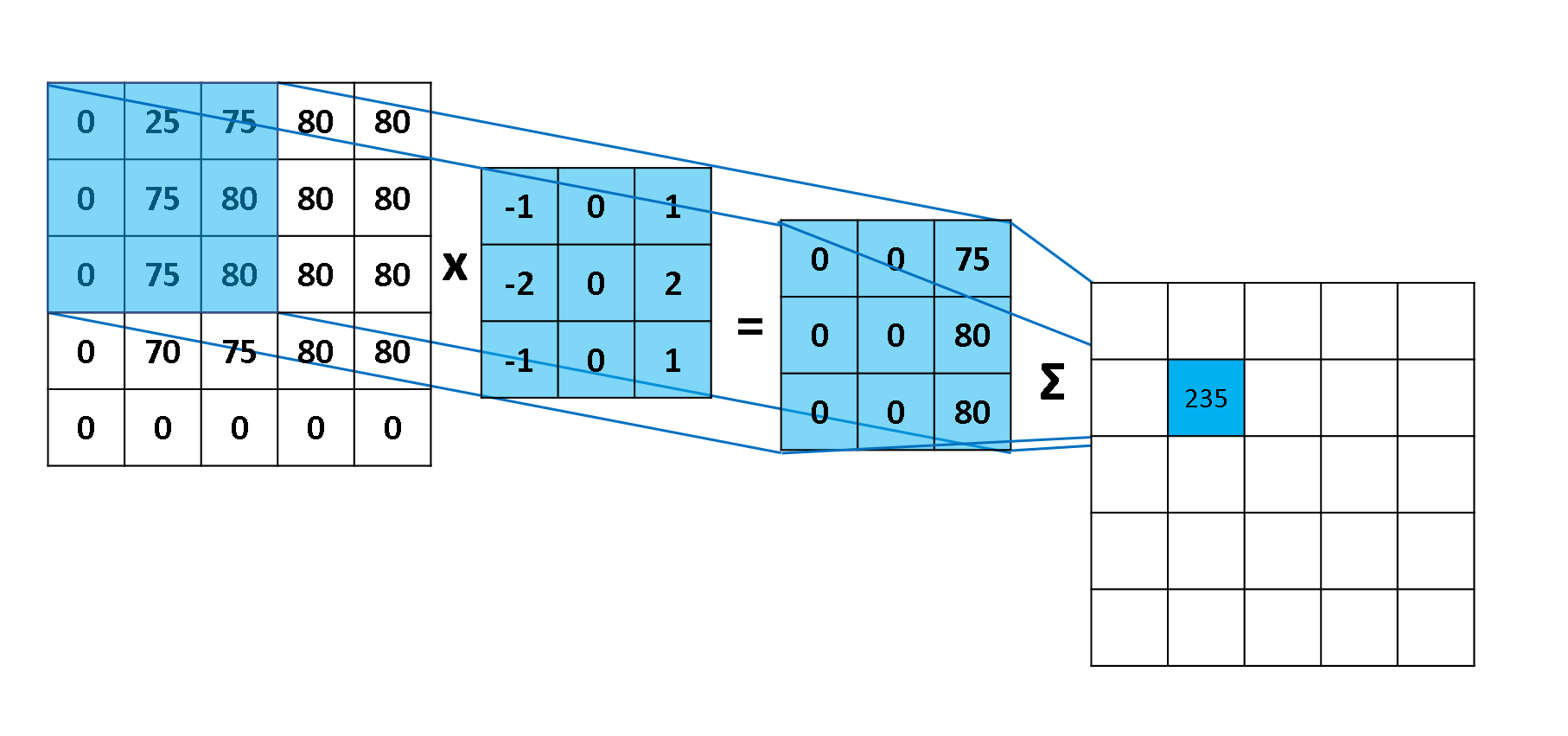
下图 15 形象的刻画了利用一个 3x3 大小的卷积核的整个卷积计算过程：

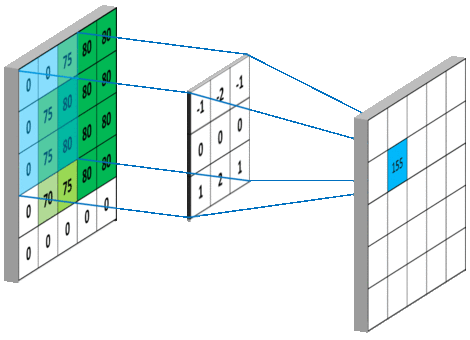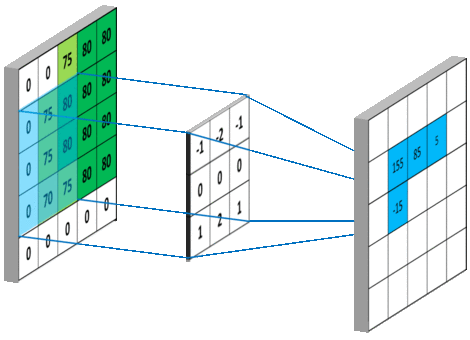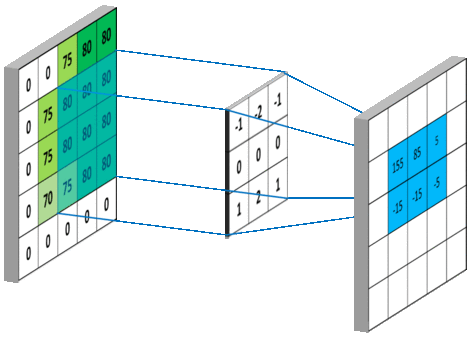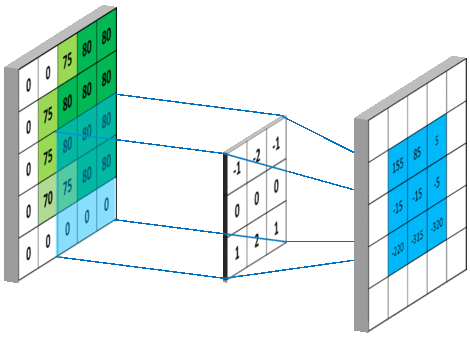
这个过程我们可以理解为我们使用**一个过滤器（卷积核）**来过滤图像的各个小区域，从而得到这些小区域的特征值。

在具体应用中，往往有多个卷积核，如：彩色图像由三原色构成，二维图像在任意一个点像素为立体三层结构，分别是红色、绿色、蓝色值，该值的范围在0∽255之间，在计算机里用一个无符号的8位数表示，有三层结构彩色图像通常也称为通道数为三层，当输入图为一张3通道彩图时，也可以理解为输入3张二维图，每个二维图通道数是1，所以在CNN里‘通道数’与输入、输出时单通道图片的个数等效。下面展示是对一个三层通道彩色图像卷积过程，这个卷积过程使用了2个卷积核，用于提取图像特定的2个特征，由于图像通道数是3所以每个卷积核也是3层结构。

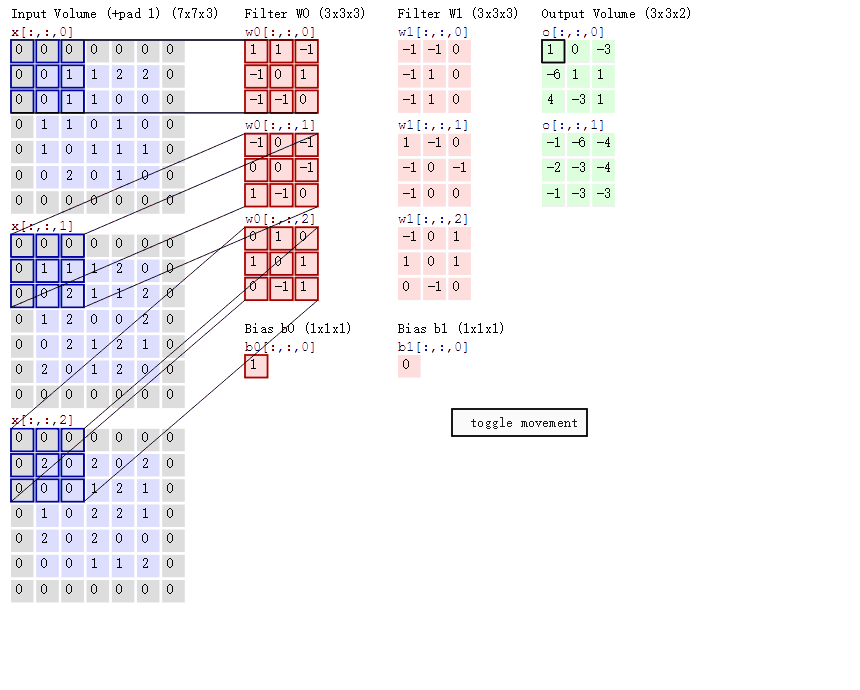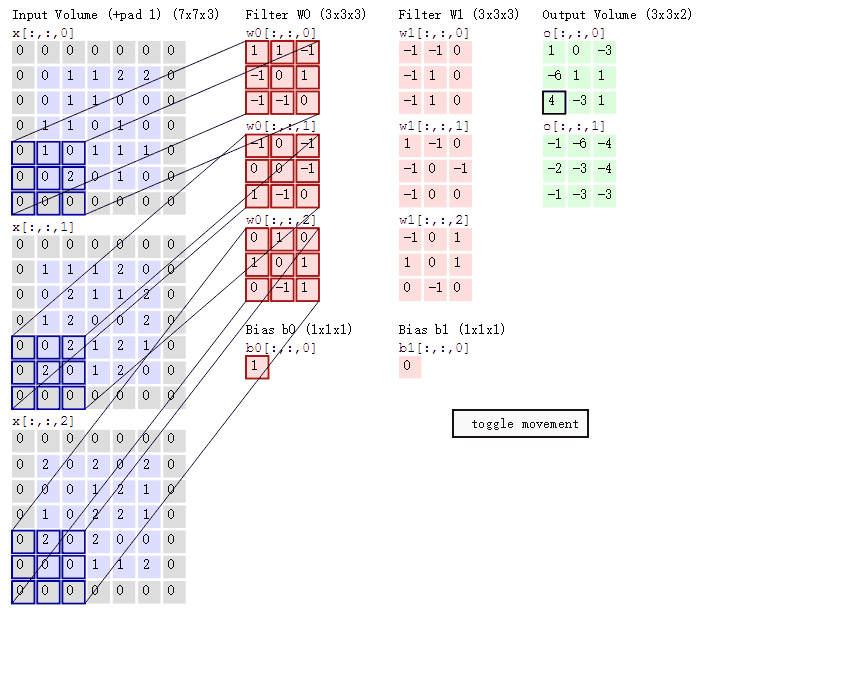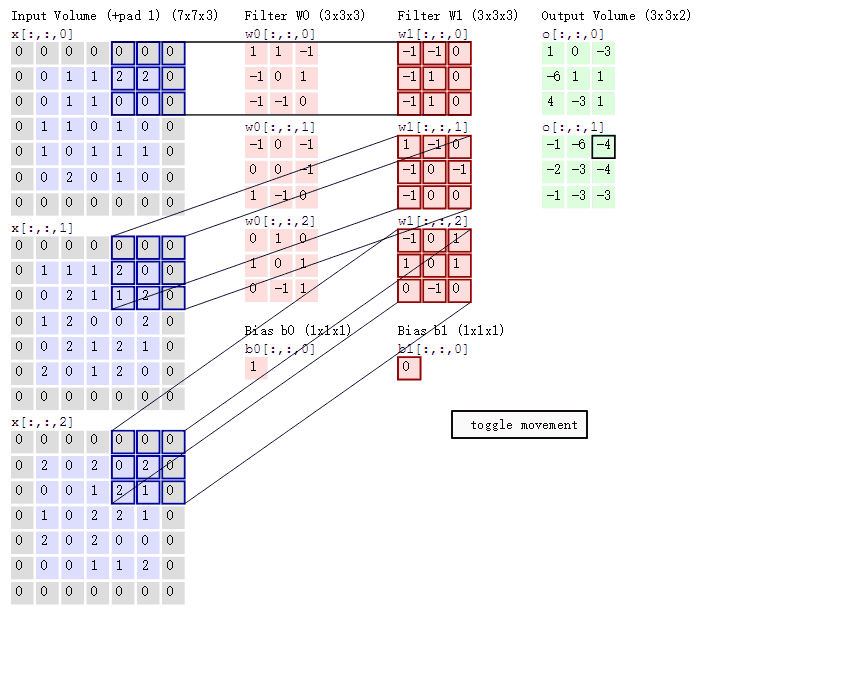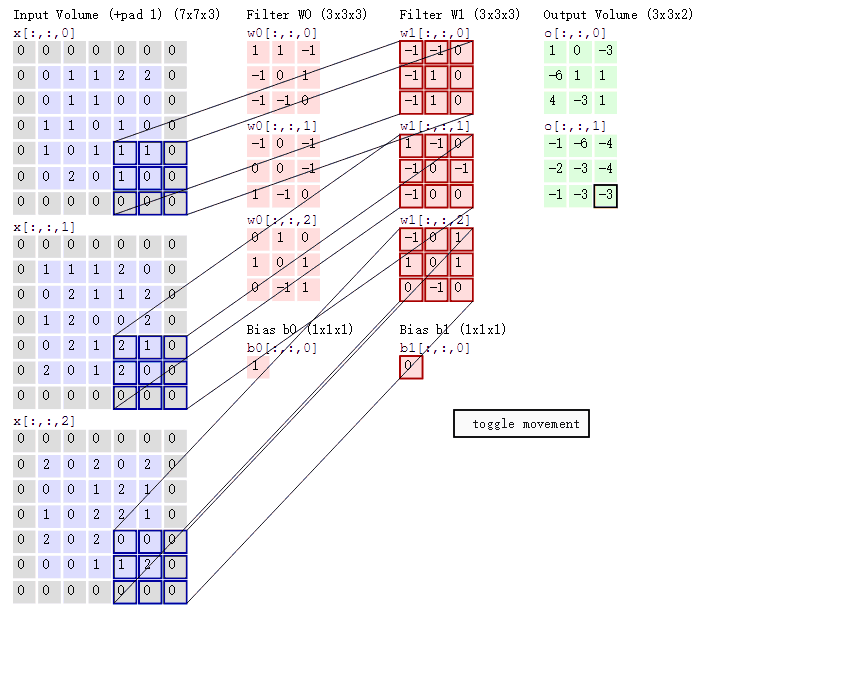
4.1.2 卷积特征值计算方法

讲一下计算过程吧：

• Input Volume中三个二维的 7 * 7分别代表 R G B三个图像层
• Filter W0中三个 卷积核 内容不同，分别对应着R G B进行运算
• 如何运算？以Input Volume中 R 与 Filter 中 R对于的W0（卷积核）来计算示例：

（0 * 1）+ （0 * 1）+ （0 * -1）+ （0 * -1） + … + （1 * 0）是每个相对应的cell去相乘，input Volume中的左上角第一个格中的值0，乘 Fiter W0中左上角第一个格中的值1，以此类推。最后得出的9个最终结果相加

​ 这只是一个颜色通道的结果，最后得出 Output Volume O_0的结果是三个颜色通道的所以结果相加===>然后别忘了加一个偏移变量b ====>最后得到Output Volume O_0最后的左上角的结果1

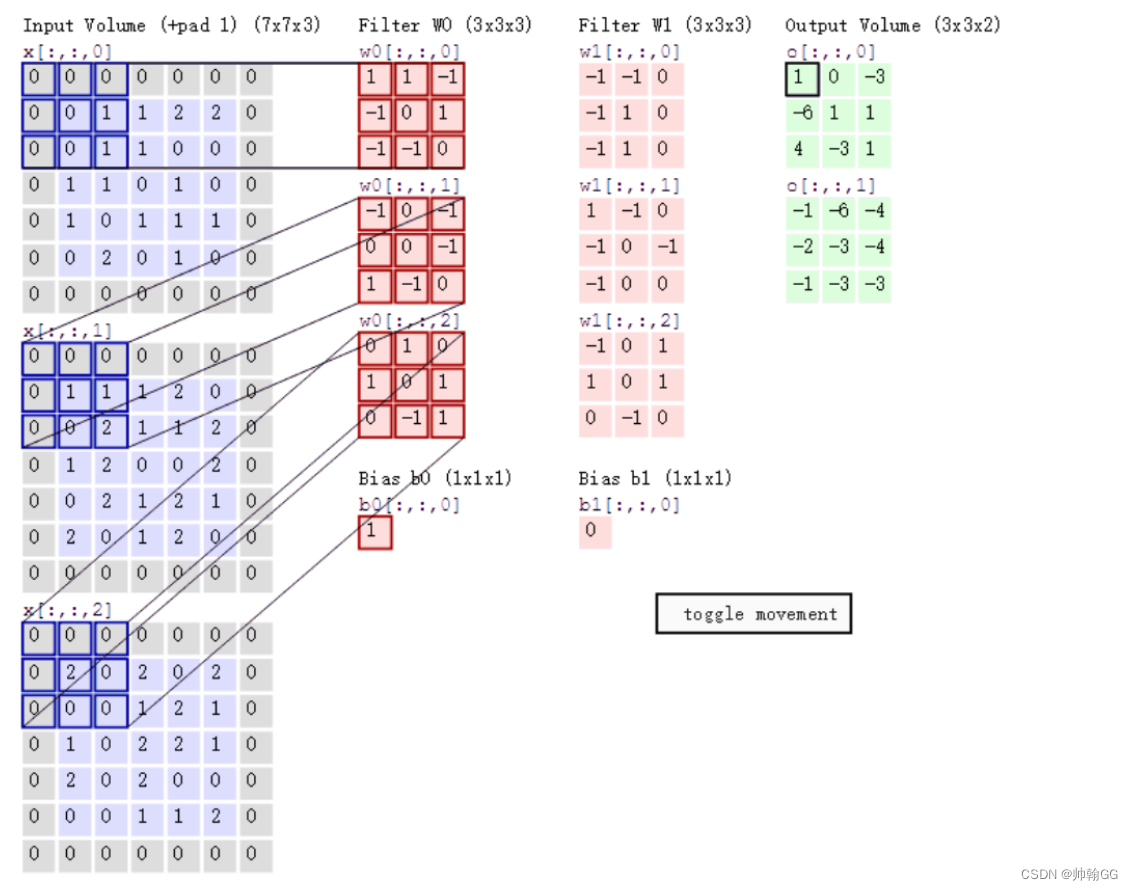
总结：卷积层的通过卷积核的过滤提取出图片中局部的特征，跟上面提到的人类视觉的特征提取类似。

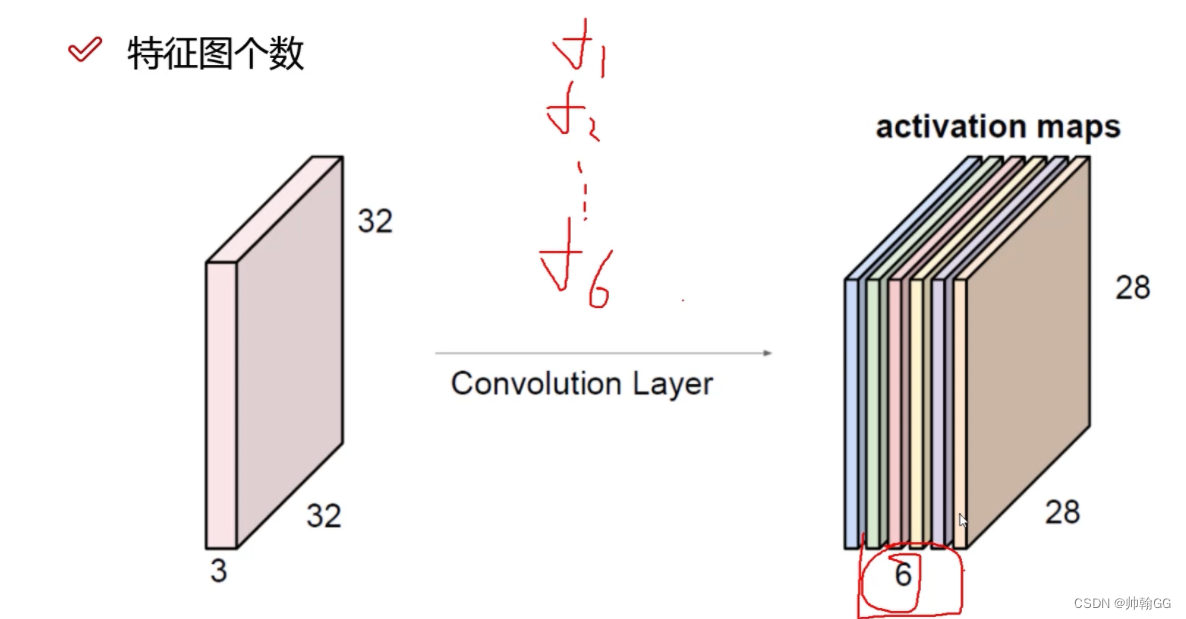
4.1.3 步长 与 卷积核 大小对结果的影响

• 卷积核

​ 类似人类的视觉原理。这里，我们先原始输入 --> 粗粒度的提取特征 --> 中粒度提取特征 --> 高粒度提取特征 -->根据最后提取出来的特征进行分类。

​ 这就说明了，我们做一次卷积是不够的，要多次迭代的做卷积。
CONV 是卷积的意思，通过一次一次的迭代卷积，得出最后的结果。
其中e.g.6 和 e.g.10分别代表 6个卷积核 10个卷积核

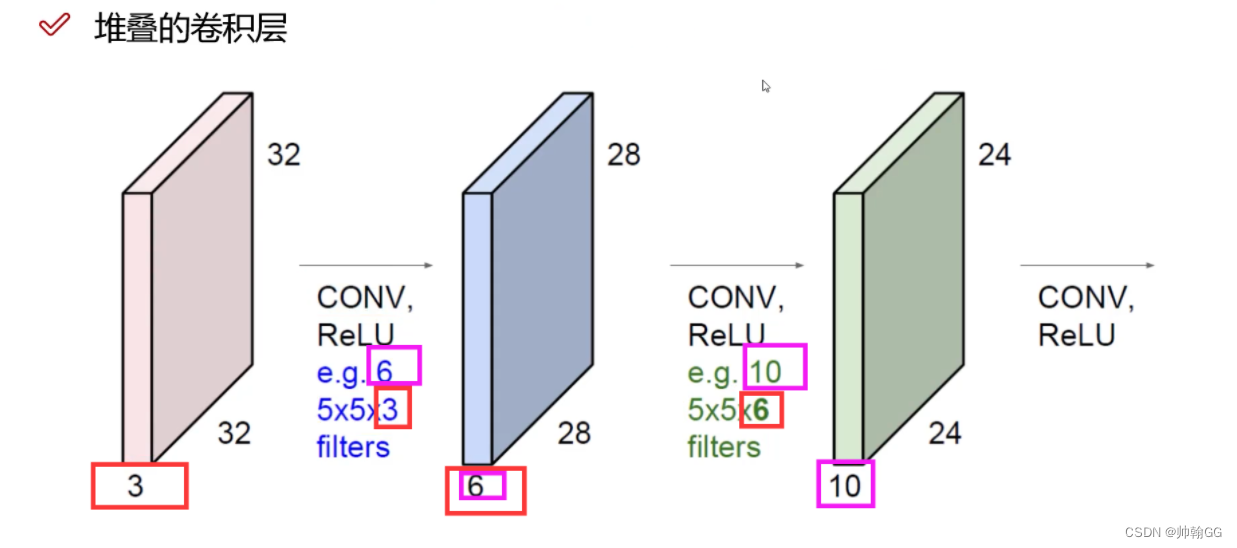
• 步长：

也适用于NLP自然语言处理

步长越大，提取的特征越少。

4.2 池化层————数据降维，避免过拟合

4.2.1 池化层的作用

​ 池化(pooling)层是将卷积后的特征图进一步降维、缩小特征图尺寸，池化后对信息是虽然有损失的，但也保证了模型有较好的拟合能力。

​ 之所以这么做的原因，是因为即使做完了卷积，图像仍然很大（因为卷积核比较小），所以为了降低数据维度，就进行下采样。

常见池化示意图如下：

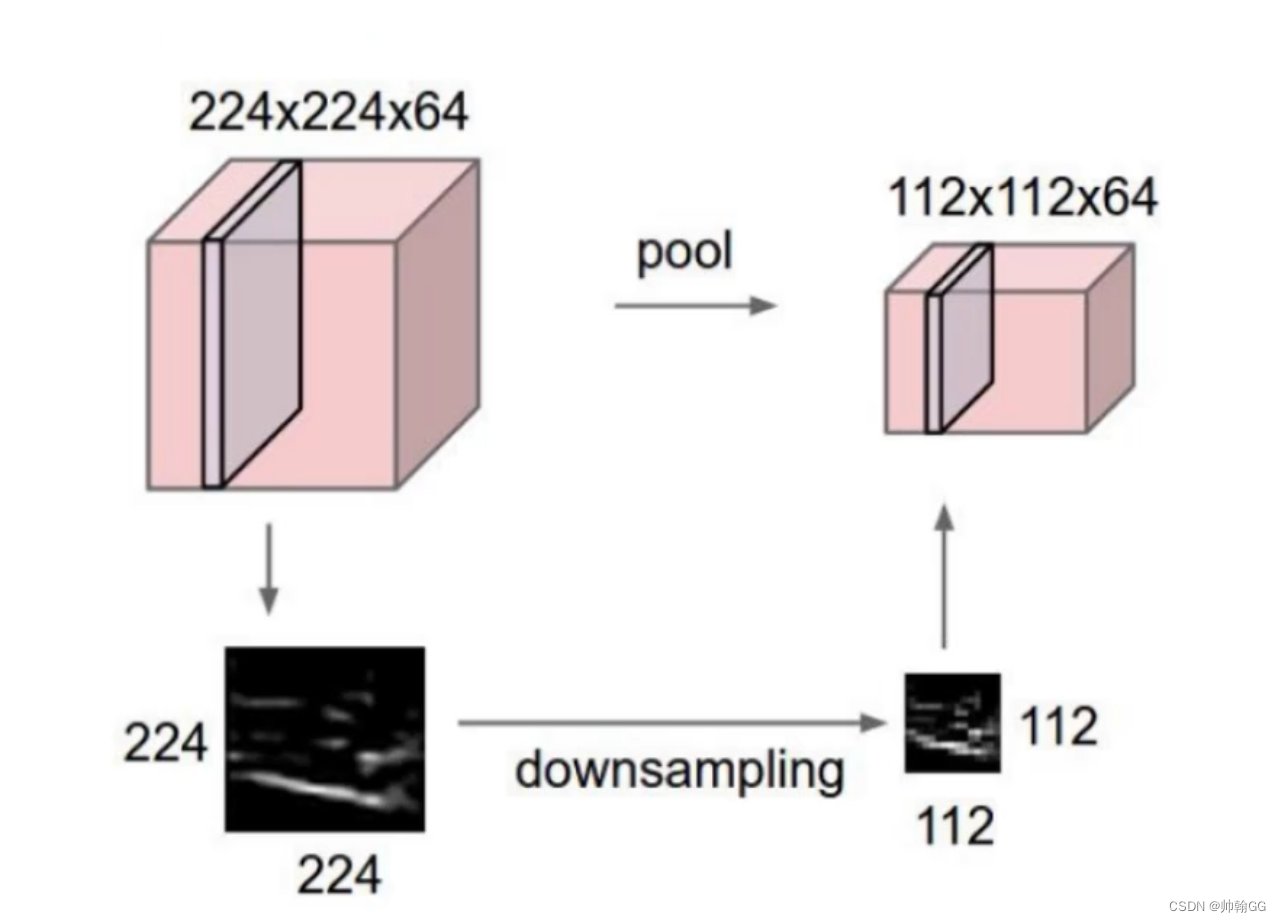
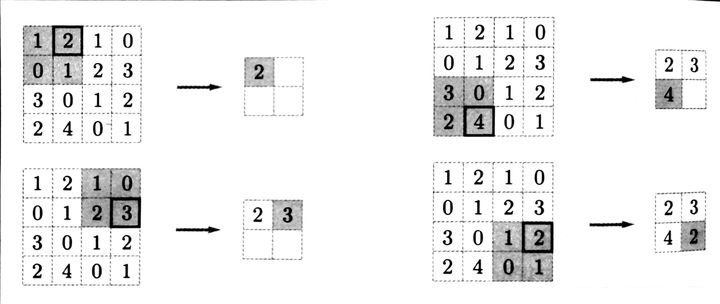
常用池化手段有最大池化法(Max pooling)、平均池化法(Average pooling),最大池化法取池化窗口内最大值作为输出，过程如下图所示：

• MAX POLLING ：选择权重大的，即：重要的点

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-on1wwAnS-1689147739700)(C:\Users\ASUS\AppData\Roaming\Typora\typora-user-images\image-20230712130244327.png)]

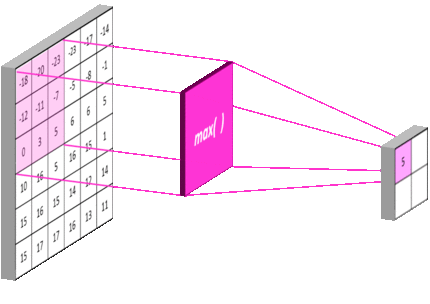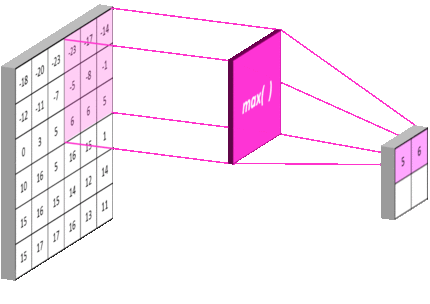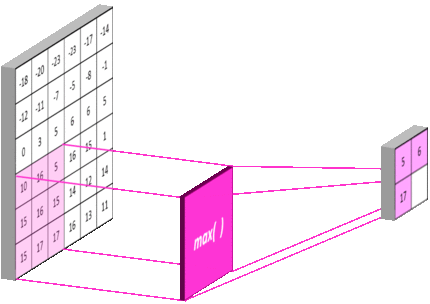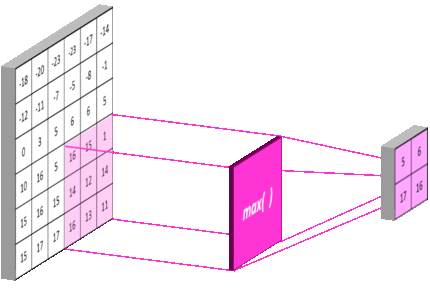
总结：池化层相比卷积层可以更有效的降低数据维度，这么做不但可以大大减少运算量，还可以有效的避免过拟合。

4.2.2 整体网络架构

CONV：卷积

RELU ：一个函数

POOL：池化

FC：全连接

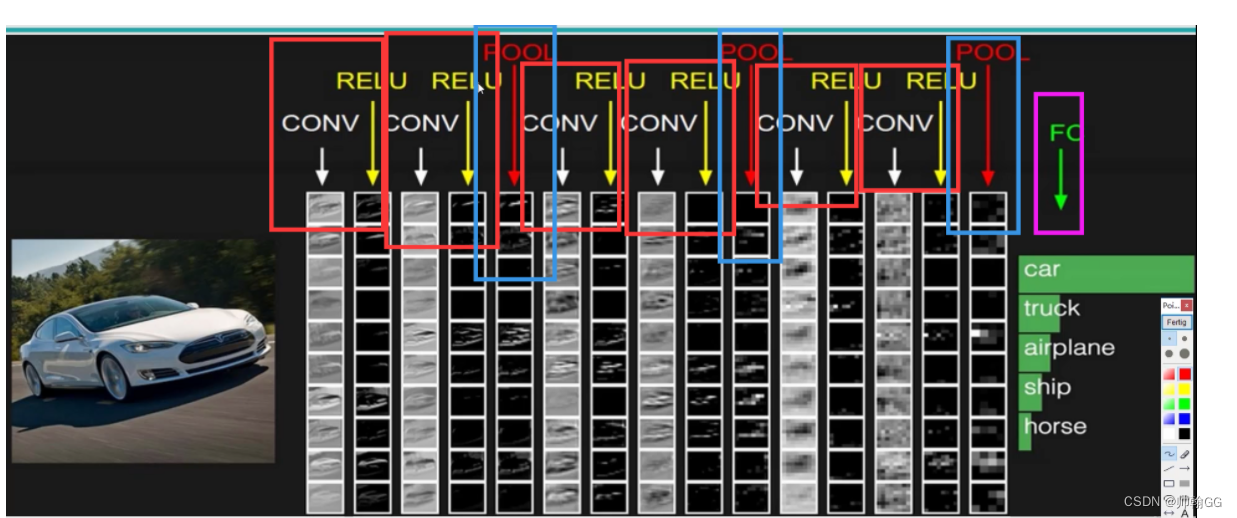
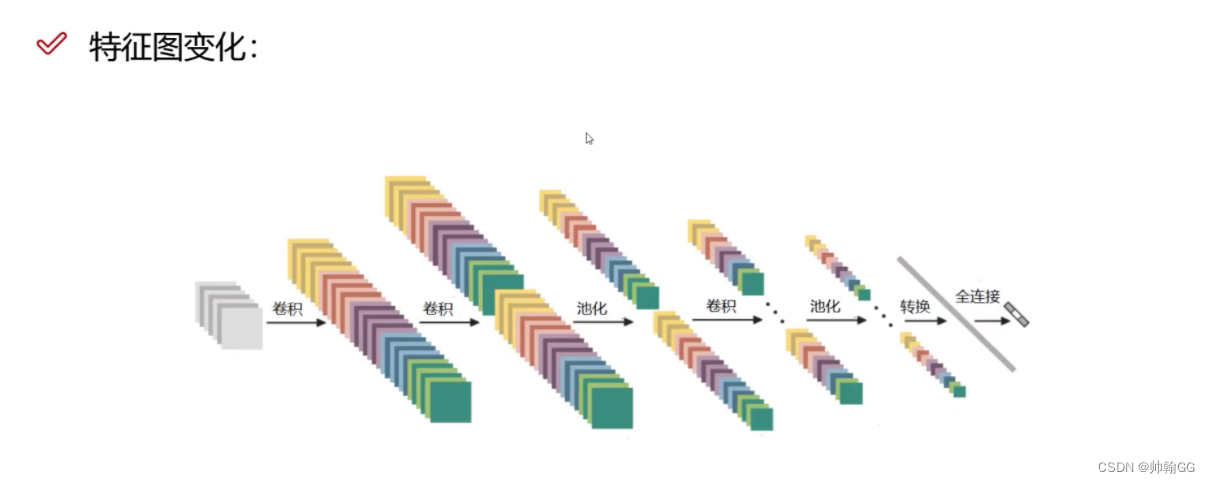
特征图的变化：

​ 卷积层 – 池化层- 卷积层 – 池化层 – 卷积层 – 全连接层

4.3 全连接层——输出结果

​ 这个部分就是最后一步了，经过卷积层和池化层处理过的数据输入到全连接层，得到最终想要的结果。

经过卷积层和池化层降维过的数据，全连接层才能”跑得动”，不然数据量太大，计算成本高，效率低下。

参考链接：
1、https://www.dohkoai.com/usr/show?id=32&catalogsortby=3
2、https://leovan.me/cn/2018/08/cnn/
3、https://easyai.tech/ai-definition/cnn/