为什么用布隆过滤器

这个是基于位图的一个超级牛皮的一个数据结构。举个例子，假设我们创建Steam账号，我们的账户名字是不允许重复的，所以我们需要找到一个没有人使用过的名字，但是我们得知道现在这个名字是否有人用过，就得去访问服务器数据库查询名字是否被使用，由于服务器的交互远程的方式，所以我们“名字”这个数据需要去服务器中查询是否重复。

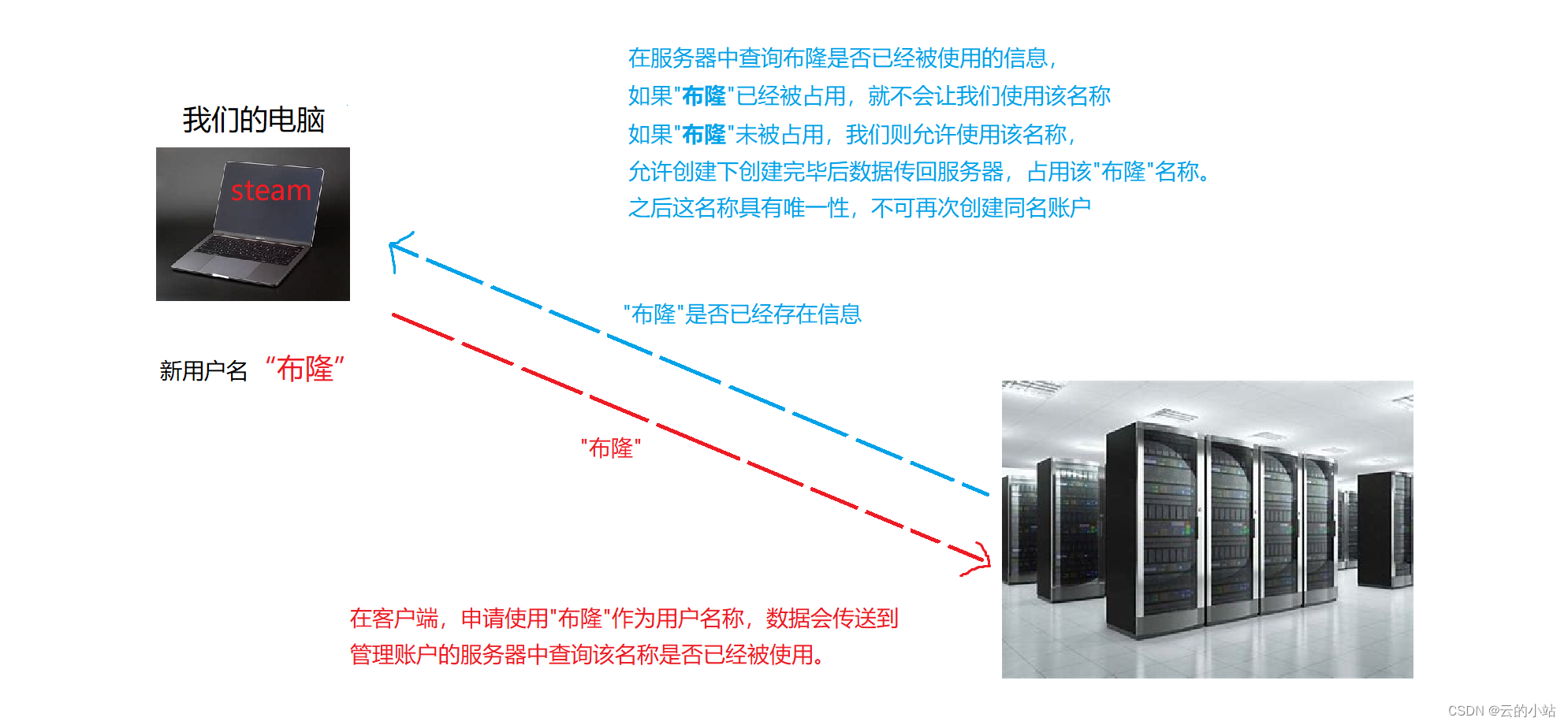
但是如果一个名字就要直接访问服务器存储空间，效率是底下的，数据在服务器是以磁盘方式存储，在远端又是磁盘存储，访问速度大大降低，你也不想一个名字访问这么久吧？

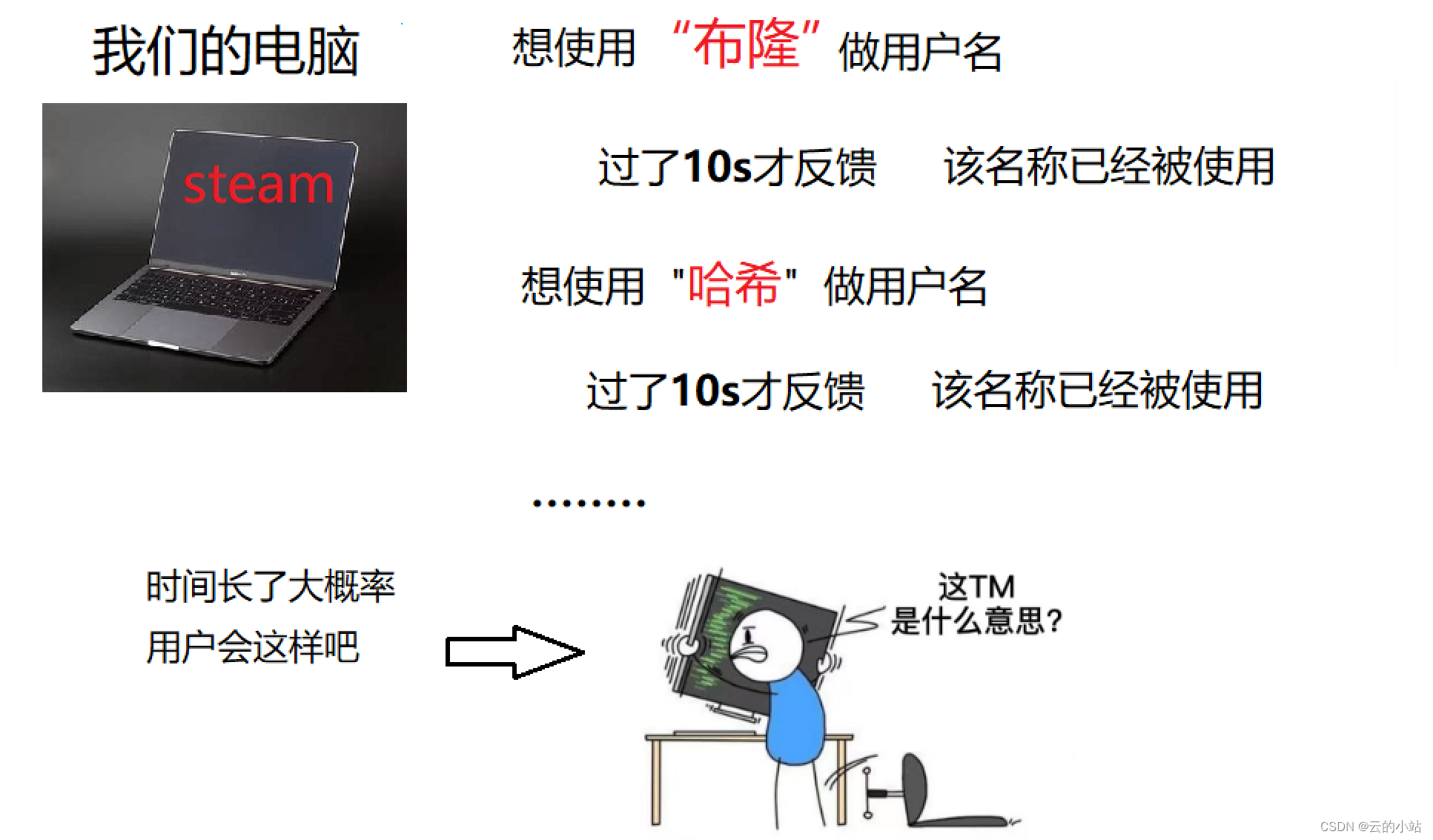
如果不想在门槛上就流失客户，我们应该加一层数据层，用来快速访问用户名是否存在的数据

记住，计算机世界问题解决不了就加一层，如果还是解决不了再加一层。

所以我们需要在服务器与客户端交互中做一个中间层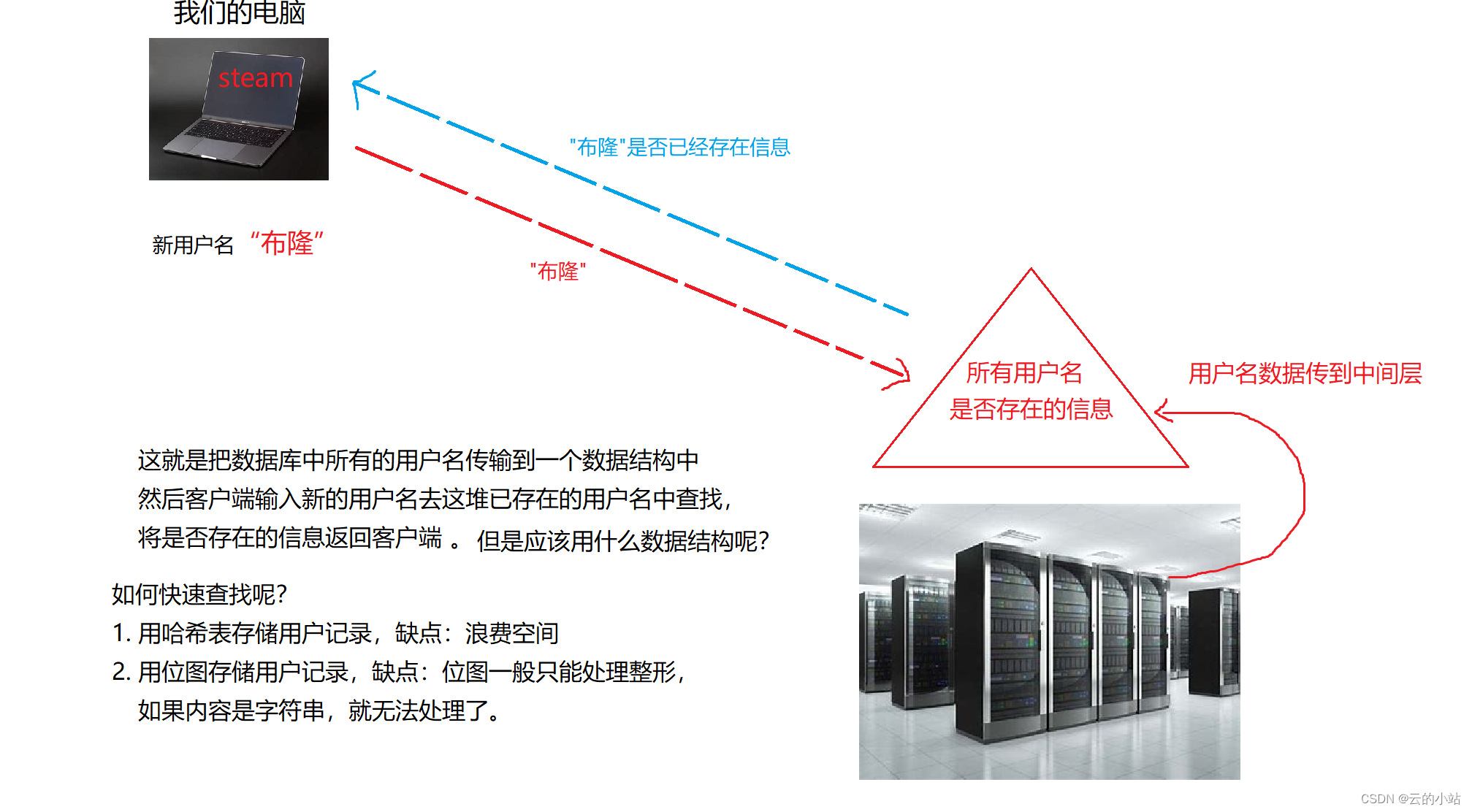

布隆过滤器原理

这时候我们的布隆过滤器运势而生！！他结合哈希算法与位图，大大提升查询速度而且节省空间，毕竟我们只是想知道这个数据是否存在于集合中，所以可以使用位图比特位来确定。

而且这也保护了数据的安全性，只有比特位数据，没有哈希算法的情况下，不会造成用户名数据外流的情况。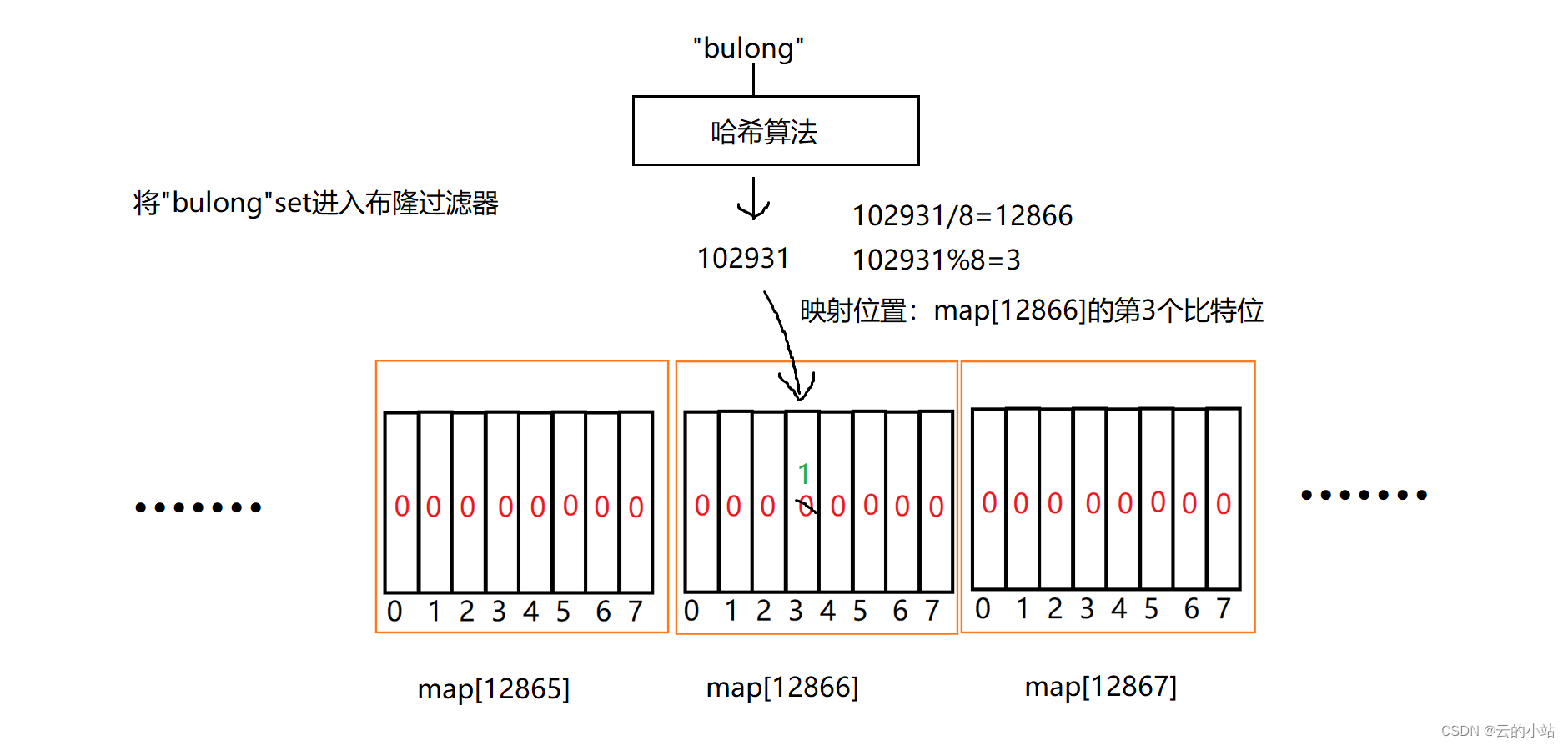

但是有一个问题有摆在我们的面前，就是可能出现误判数据的情况。如果这时候来了一个新的字符串需要映射但是在哈希算法后的到的数字也是102931呢？

这个时候我们就不能只以一个比特位为一个标识位，根据大佬数学推算出开---开数据范围5倍的空间时，既节省空间有大大降低了误判率（为什么不是准确呢？应为哈希算法是将字符串转换为下标数字，既然是字符串转换数字，就一定有可能存在两个字符串转换相同的数字情况），我们需要增加不同的哈希算法数量，保证了多位映射（多位映射也无法避免误判）。

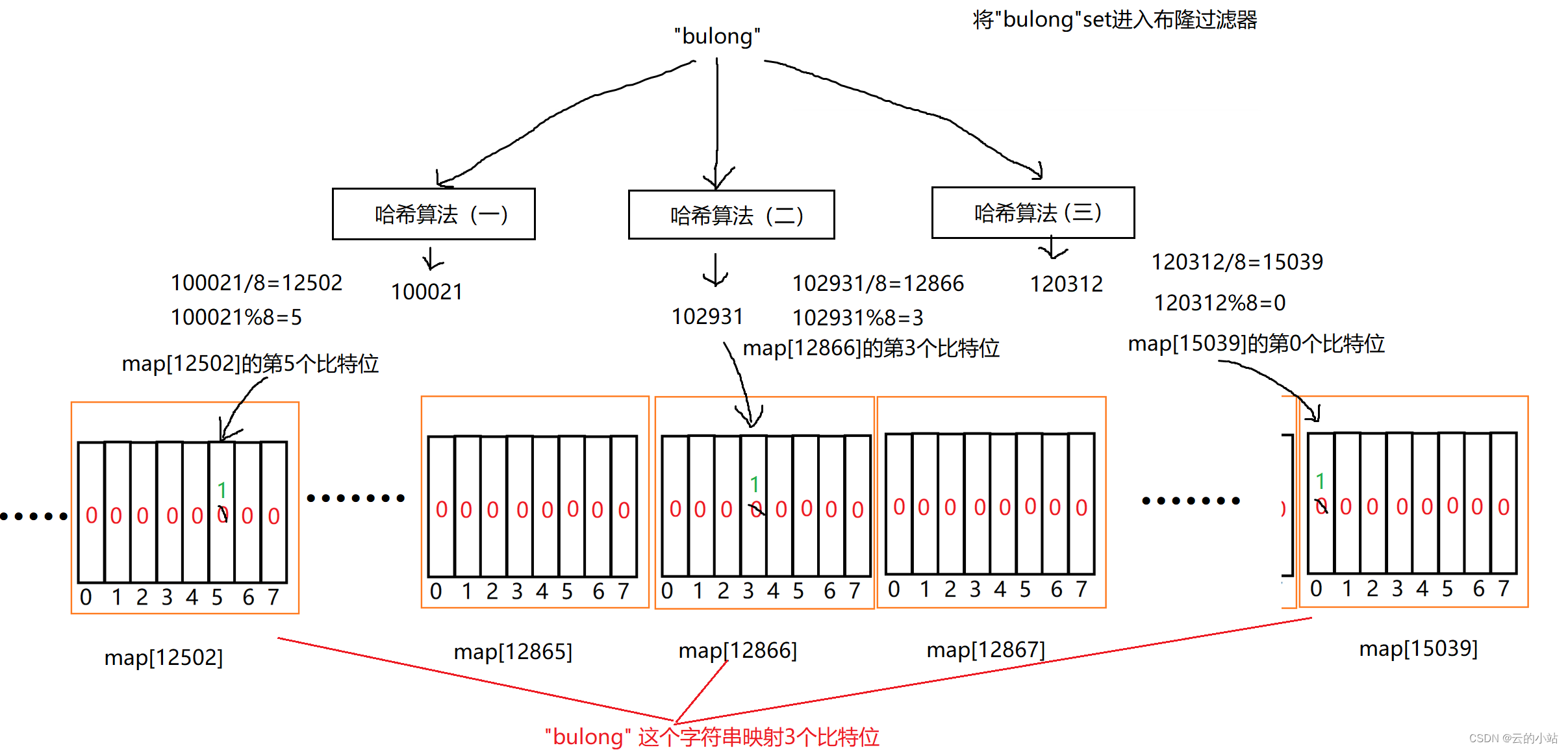
这样尽管不同的字符串映射后有一位比特位，和其他字符串映射比特位相同，那么依旧有其他位的映射，只有所有位都映射了才说明，该字符串已被标记在布隆过滤器中。

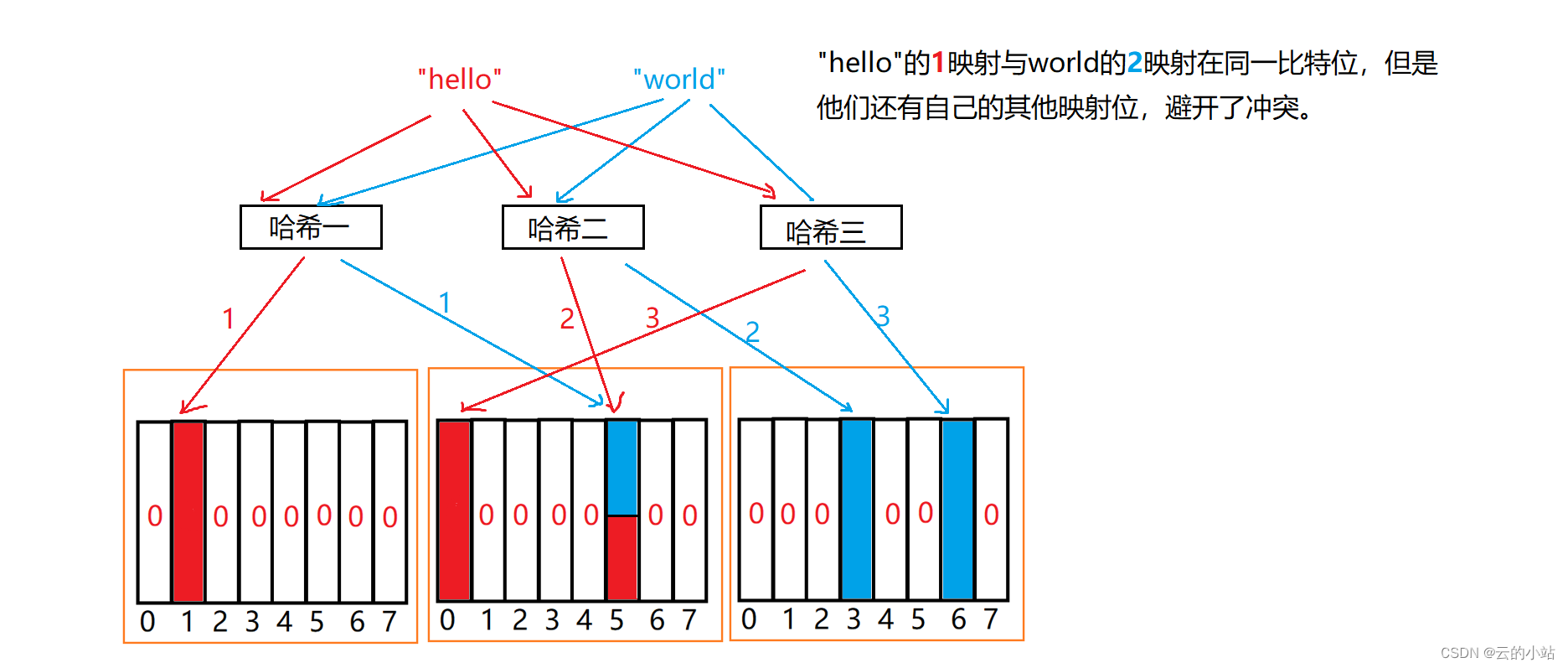
但是有一个误判情况是避免不了的。假设我们的布隆表已创建完毕，现在需要查询一个字符串“Finish”是否在集合中存在，原本该字符串是不存在的，但是通过3个哈希算法得出的整型映射的位都被其他映射的占用了，会出现存在的假象-->误判。

所以误判行为是无法避免的，字符串可能性是无穷无尽的，我们的映射位有可能被多个数据所映射着，所以布隆过滤器也有所不足，当时作为数据库的辅助工具足以。

举个例子：信用黑名单毕竟是少数人，将失信名单从数据库放入布隆过滤器中，如果来了个人查询，

如果布隆中不存在，就不用再去访问数据库，直接返回不在黑名单

如果布隆中是存在，再去数据库核实是否真实存在，再将结果返回，毕竟这可是大事，不能误判。

再举了个例子：

游戏名字不可重复，数据库会将所有游戏名都放入布隆过滤器中，玩家创建名字的时候，会拿着名字取布隆过滤器中查看，这个名字不存在就允许创建，名字存在就直接返回不让创建，但是误判也没啥，直接返回告诉玩家换个昵称就好。

代码：

template<class K,size_t N,class Hash1, class Hash2, class Hash3>
//三个哈希算法帮我们映射位
class BloomFilter
{
public:
	void set(const K&key)
	{
		size_t hash1 = Hash1(key) % (_ratio * N);
		_bits.set(hash1);
		size_t hash2 = Hash2(key) % (_ratio * N);
		_bits.set(hash2);
		size_t hash3 = (Hash3(key) % (_ratio * N);
		_bits.set(hash3);
        //映射3个比特位
	}
	bool test(const K& key)
	{
		size_t hash1 = Hash1(key) % (_ratio * N);
		if (!_bits.test(hash1))
			return false;
		size_t hash2 = Hash2(key) % (_ratio * N);
		if (!_bits.test(hash2))
			return false;
		size_t hash3 = Hash3(key) % (_ratio * N);
		if (!_bits.test(hash3))
			return false;
        //查询数据的时候，3个位都得查看，但凡一个不存在就直接返回false
		return true;
        //存在或者误判存在
	}

private:
	const static size_t _ratio = 5;//开5倍的空间
	bitset<ratio*N> _bits; //位图当底层结构
};