源码解析Collections.sort ——从一个逃过单测的 bug 说起

本文从一个小明写的bug 开始，讲bug的发现、排查定位，并由此展开对涉及的算法进行图解分析和源码分析。

事情挺曲折的，因为小明的代码是有单测的，让小明更加笃定自己写的没问题。所以在排查的时候，也经历了前世的500年，去排查排序后的list改动（主要是小明和同事互相怀疑对方的代码，不多说了）。

本文从问题定位之后开始讲：

前言

小明写了一个自定义排序的代码，简化后如下。聪明的你快来帮小明review一下吧。

代码

背景：有一组商品，status是状态，其中2表示有货，9表示区域无货，5表示已抢光。需要按照 2 有货< 9 区域无货< 5 已抢光的顺序进行排序。

例如：输入：[2, 9, 5, 5, 9, 2, 9]，期望输出：[2, 2, 9, 9, 9, 5, 5]。list不为空，数量小于100。

环境：JDK 8

小明的代码如下：

/**
* 排序
*/
private static int compare(Integer status1, Integer status2) {
        // 5大于9 大于2 ，按照这样的规则排序
        if (status2 != null && status1 != null) {
            // 5-已抢光, 已抢光排到最后面
            if (status2.equals(5)) {
                return -1;
            } else {
                // 9-区域无货, 区域无货排在倒数第二，仅在已抢光之前
                if (status2.equals(9) && !status1.equals(5)) {
                    return -1;
                }
            }
        }
        return 0;
    }

  //Test 
  public static void main(String[] args) {
       List<Integer> list = Lists.newArrayList(2, 9, 5, 5, 9, 2, 9);
        System.out.println("排序前:"+list);
        list.sort(Test::compare);
        System.out.println("排序后:"+list);
    }

看上面的代码有问题么？别急，咱们先给个入参试一下。

测试

[ 2, 9, 5, 5, 9, 2, 9 ]

 public static void main(String[] args) {
       List<Integer> list = Lists.newArrayList(2, 9, 5, 5, 9, 2, 9);
        System.out.println("排序前:"+list);
        list.sort(Test::compare);
        System.out.println("排序后:"+list);
    }

输出：

排序前:[2, 9, 5, 5, 9, 2, 9]
排序后:[2, 2, 9, 9, 9, 5, 5]

结论：结果是对的，符合预期 。 （ 按照 2 有货< 9 区域无货< 5 已抢光的顺序进行排序） 。

---

嗯，看起来排序是对的。但确实是有问题呢？

（小明OS ：哪里有问题？不可能有问题！我本地是好的！）

那我们看看情景复现👉🏻

---

情景复现

那有什么问题呢？我们再给几个入参试一下 。

case1 : 随机入参

[5, 9, 2, 5, 9, 9, 9, 5, 2]
输出：

排序前:[5, 9, 2, 5, 9, 9, 9, 5, 2]
排序后:[2, 2, 9, 9, 9, 9, 5, 5, 5]
期望是:[2, 2, 9, 9, 9, 9, 5, 5, 5]

结论：结果对，符合预期 ✅。

case2 : 多增加一些数

[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 5, 5, 5, 5, 5, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 9, 5, 5]

输出：

结论：结果不对了，不符合预期 ❌。

case3 : 换几个数

[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 9, 9, 9, 9, 9, 5, 5, 5, 5, 5, 9, 9, 9, 9, 5, 5]

输出：

结论：结果又对了？？

这是什么情况？!

小明有些慌了，越想越觉得奇怪，目前看起来有这样几个看起来些许离谱的结论：

1、可能是和数据量有关系（因为用32位以下的数据，多次Test 也没发现问题），

2、一定和数据数值有关系。（32位以上，有的数据样本没问题，有的有问题）。

3、有问题都在中间部分，而两边是有序的，猜测像排序归并导致的问题。

定位

想查这个问题，小明有三个思路。

一是：代码的逻辑比较，是有一些不完整的。那可以先试着改改代码，通过这几个失败用例，然后在找深层原因。

二是：查查用的排序类，有没有坑。用法有没有特殊注意的，有没有类似的案例。

三是：从源码上，理清排序底层的逻辑，找到哪一个环节排序出了问题。

顺着这三个思路，小明发现写的代码里缺少返回为1的场景。虽然小明不知道有没有影响，但是试了试，发现好使。。但为啥呢？

private static int compare(Integer status1, Integer status2) {
        // 5大于9 大于2 ，按照这样的规则排序
        if (status2 != null && status1 != null) {
            // 5-已抢光, 已抢光排到最后面
            if (status2.equals(5)) {
                return -1;
            } else {
                // 9-区域无货, 区域无货排在倒数第二，仅在已抢光之前
                if (status2.equals(9) && !status1.equals(5)) {
                    return -1;
                }**else{
										return 1;
								}**
            }
        }
        return 0;
    }

然后小明看 Collections.sort 的坑，没有看到和这个相关的。

接下来，还是要来调试代码。最终定位是因为原来的compare 自定义代码里，对 compaer(5,2) 这种应该返回1的情况 ，默认返回了0。导致在底层两组数据归并排序过程，误以为5和2相等了。

即导致了这样错误的结果:

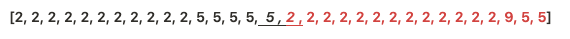
见Debug部分：（具体分析内容在后边源码部分）

解决方案

发现问题，就好解决了。方案是，要么补充完善逻辑，要么换用一种权重映射的排序方式。

1 优化代码

private static int compare(Integer status1, Integer status2) {
        // 5大于9 大于2 ，按照这样的规则排序
        if (status2 != null && status1 != null) {
            // 5-已抢光, 已抢光排到最后面
            if (status2.equals(5)) {
                return -1;
            } else {
                // 9-区域无货, 区域无货排在倒数第二，仅在已抢光之前
                if (status2.equals(9) && !status1.equals(5)) {
                    return -1;
                }else{
										return 1;
								}
            }
        }
        return 0;
    }

2 改为权重等方式排序

当然，还有对于一些容易理解出错的排序，也可以通过设置权重映射的方式进行排序。

小明忽然想起来，无论底层排序算法是什么， 排序逻辑还是要完整。这一点也开发规约也是有的呀。 👉🏻

【注意】在JDK7版本及以上，为了让Arrays.sort、Collections.sort正常工作，Comparator必须满足以下三个条件，否则会抛出IllegalArgumentException异常。

1）比较x和y的结果应该与比较y和x的结果相反。
2）如果x>y，y>z，则x>z。
3）如果x=y，则比较x和z的结果应该与比较y和z的结果相同。

好了问题解决了，那我们接下来慢慢聊聊这里Collections.sort 底层用的TimSort排序原理。以及为什么32位及以上才有问题，为什么正好是归并过程有问题 ？

---

源码解读

---

JAVA 7 中集合类中的sort 开始，默认用TimSort排序方法 。Tim Sort，里的Tim 也没什么特别的含义。Tim是这个算法的创始人Tim Peters 的名字。该算法首先在Python中应用，之后在 java 中应用。

TimSort ：一种稳定的、自适应的、迭代的归并排序，在部分排序数组上运行时需要的比较远远少于nlg (n)次，而在随机数组上运行时提供与传统归并排序相当的性能。像所有合适的归并排序一样，这种排序是稳定的，运行时间为O(n log n)(最坏情况)。在最坏的情况下，这种排序需要n/2个对象引用的临时存储空间;在最好的情况下，它只需要少量的常量空间。这个实现改编自Tim Peters的Python列表排序

图解 TimSort 排序原理

如果数组的长度小于32，直接采用二分法插入排序。（略）

如果数组的长度大于32，找到 单调上升段（或下降段，进行反转），然后基于这个单调片段，通过插入排序的方式进行合并。如此反复归并相邻片段。

到这一步的时候，小明恍然大悟，怪不得32位数以下，没有出现过问题呢。

这个算法里有一个重要的概念，也可以理解为分段( 算法里 run )。每个分段都是连续上升或下降的子串

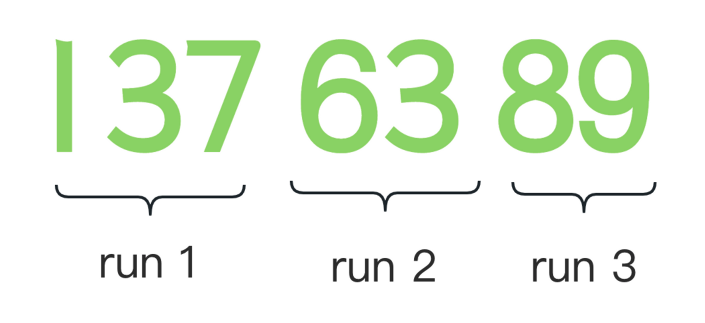
然后对下降的分段进行反转，使其变为一个递增的子串。这样就可以得到若干的分段，使得每个分段都单调递增，后续就可以对这些分段进行合并。

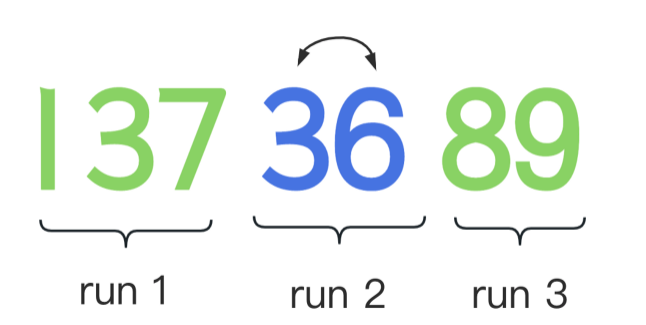
👉🏻 当然算法里会计算出一个最小的分段长度（Java里16-32之间），来控制分段的数量以保证效率。对那些不满足最小长度的分区，会采用二分插入的方法，使其满足最的长度。比如我们假设最小的长度是3，那此时由于第二段36 不符合最小长度3，会利用二分插入法，将8插入到第二段。即 368 就是第二段了。

分段划分之后，下一步就是如何进行合并。

合并时，会将分区进行压栈，并判断是否需要和之前的分段做合并。当然还有一些更详细的优化点，具体可看下文源码部分。重点说一下，两个分段如何进行合并。

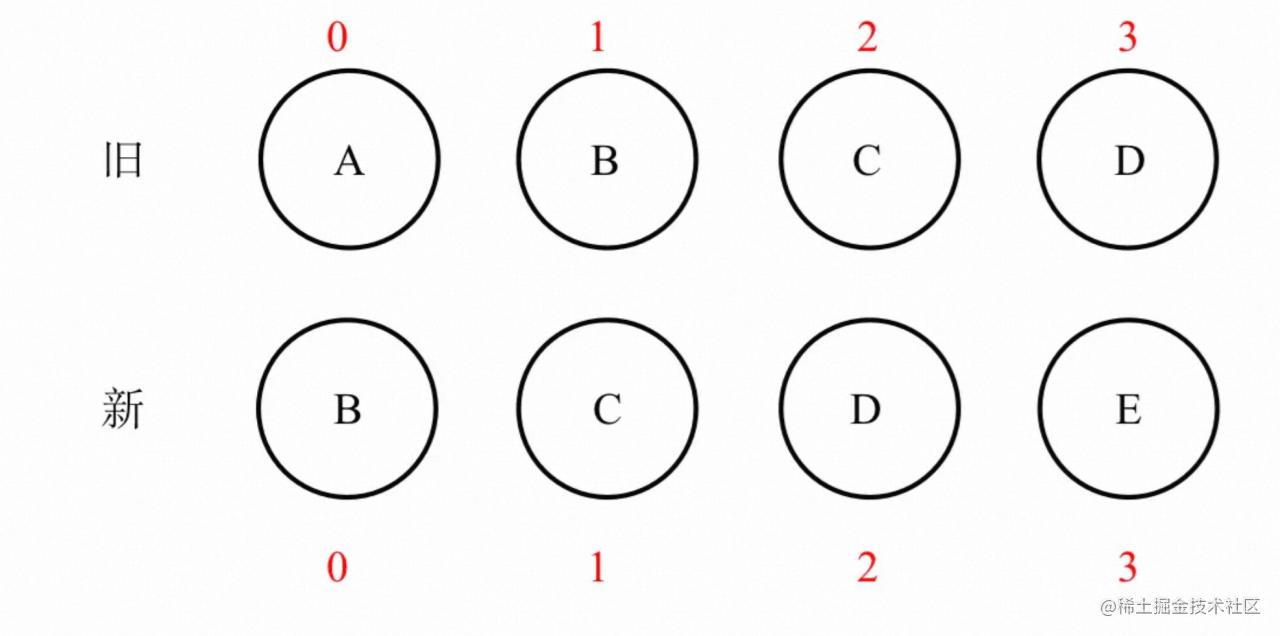
假设以下内容：

第一个段包含元素：[1,2,3,5,6,8,9]

第二个段包含元素：[4,6,7,8,10,11,12]

第一个段在数组中出现在第二个段之前。请注意，实际段落长度不会这么短。如前所述，段落长度应介于16到32之间。此处只是提供示例以说明问题。

gallopRight()：查找第二个段的第一个元素在第一个段中的位置。例如，在此示例中，位置为2。这意味着前两个元素不需要参与合并，它们的位置不需要改变。

gallopLeft()：查找第一个段的最后一个元素在第二个段中的位置。在此处，发现第二个段中的第四个元素为10。因此，第二个段中的10、11、12不需要参与合并，它们的位置也不需要改变。

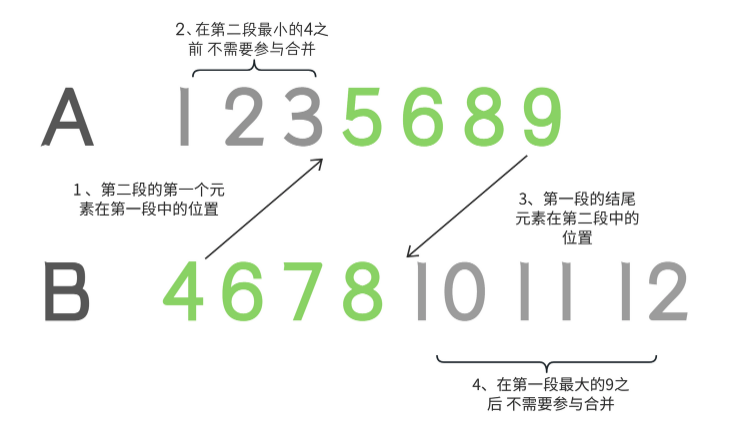
最终参与合并的段为：

第一段：[5，6，8，9]

第二段：[4, 6, 7, 8]

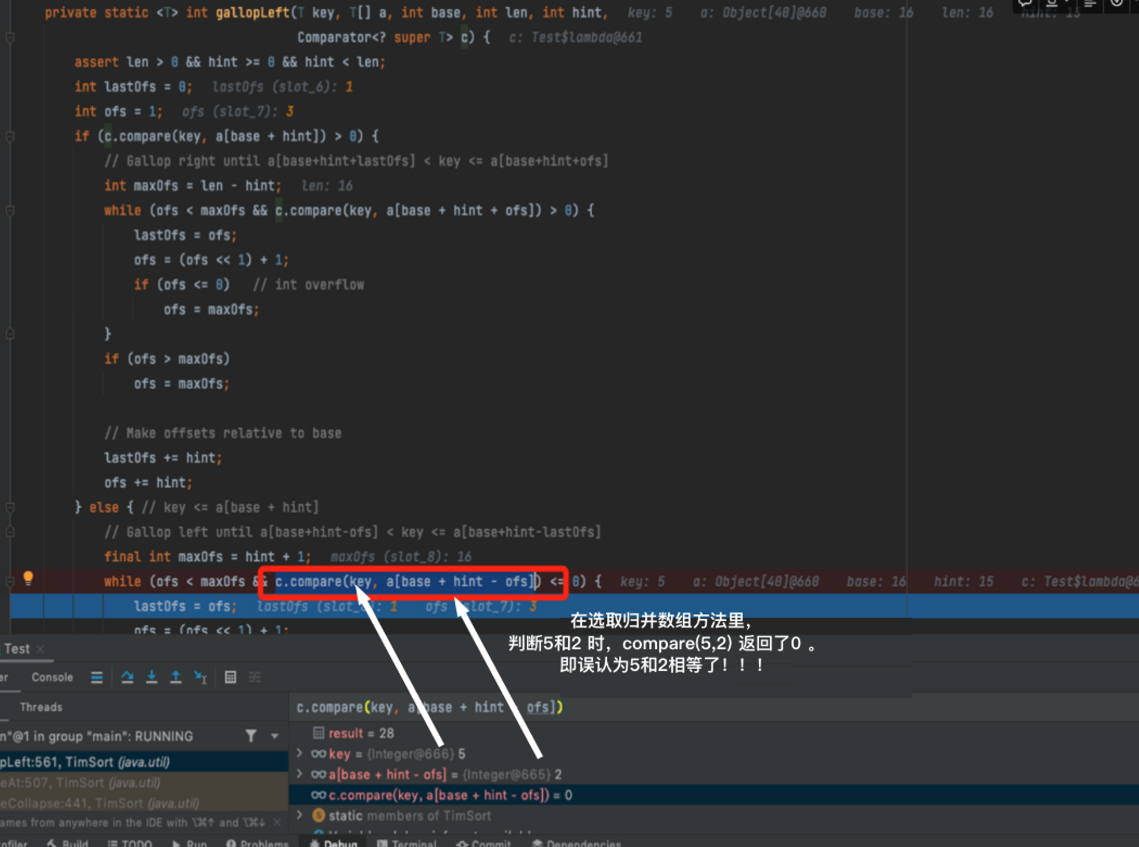
这样参与合并的段的长度就大大减小了。 这里就是我们上边问题出现的地方。在gallopLeft 方法里，

查找第一个段的最后一个元素【5】在第二个段中的位置时，比较【5】和【2】时，得出了相等的结果。这有什么影响呢？因为数组分段是单调递增的，也就是说第一组里最后一个（最大的）数据5，和第二组里第一个（最小的）数据2 相等。那也就是说，第一个数组直接在第二个数组之前。即：

---

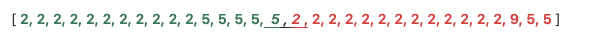
源码解读：Collections.sort 排序原理

入口

list.sort(Test::compare);

进入list sort

public void sort(Comparator<? super E> c) {
    final int expectedModCount = modCount;  // 当前 modCount 的值
    Arrays.sort((E[]) elementData, 0, size, c);  // 使用 Arrays.sort 对 elementData 数组进行排序
    if (modCount != expectedModCount) {  // 检查排序过程中是否发生了并发修改
        throw new ConcurrentModificationException();
    }
    modCount++;  // 增加 modCount 的值，表示进行了一次修改
}

Arrays.sort()

进入Arrays.sort()方法

public static <T> void sort(T[] a, int fromIndex, int toIndex, Comparator<? super T> c) {
    if (c == null) {
        sort(a, fromIndex, toIndex);  // 如果比较器为 null，调用默认的排序方法
    } else {
        rangeCheck(a.length, fromIndex, toIndex);  // 检查 fromIndex 和 toIndex 的范围是否合法
        if (LegacyMergeSort.userRequested)
            legacyMergeSort(a, fromIndex, toIndex, c);  // 如果指定使用传统的归并排序，则调用该方法
        else
            TimSort.sort(a, fromIndex, toIndex, c, null, 0, 0);  // 否则，调用 TimSort 进行排序
    }
}

TimSort.sort

我们重点看 TimSort.sort

/**
     * Sorts the given range, using the given workspace array slice
     * for temp storage when possible. This method is designed to be
     * invoked from public methods (in class Arrays) after performing
     * any necessary array bounds checks and expanding parameters into
     * the required forms.
     *
     * @param a the array to be sorted
     * @param lo the index of the first element, inclusive, to be sorted
     * @param hi the index of the last element, exclusive, to be sorted
     * @param c the comparator to use
     * @param work a workspace array (slice)
     * @param workBase origin of usable space in work array
     * @param workLen usable size of work array
     * @since 1.8
     */
    static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
                     T[] work, int workBase, int workLen) {
    assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;

    int nRemaining  = hi - lo;
    if (nRemaining < 2)
        return;  // 数组长度为 0 或 1 时，无需排序

    // 如果数组长度较小，执行“迷你的 TimSort”而不进行合并操作
    if (nRemaining < MIN_MERGE) {
        int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
        binarySort(a, lo, hi, lo + initRunLen, c);
        return;
    }

    /**
     * 从左到右遍历数组一次，找到自然的 run，
     * 将短的自然 run 扩展到 minRun 的长度，并合并 run 以保持栈的不变性。
     */
    TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
    int minRun = minRunLength(nRemaining);
    do {
        // 确定下一个 run
        int runLen = countRunAndMakeAscending(a, lo, hi, c);

        // 如果 run 很短，则扩展到 min(minRun, nRemaining) 的长度
        if (runLen < minRun) {
            int force = nRemaining <= minRun ? nRemaining : minRun;
            binarySort(a, lo, lo + force, lo + runLen, c);
            runLen = force;
        }

        // 将 run 推入待处理 run 栈，并可能进行合并
        ts.pushRun(lo, runLen);
        ts.mergeCollapse();

        // 前进以找到下一个 run
        lo += runLen;
        nRemaining -= runLen;
    } while (nRemaining != 0);

    // 合并所有剩余的 run 以完成排序
    assert lo == hi;
    ts.mergeForceCollapse();
    assert ts.stackSize == 1;
}

countRunAndMakeAscending : 找到数组中的一段有序数字

countRunAndMakeAscending：方法的主要作用就是找到数组中的一段有序数字，并告诉我们它们的长度。如果这段数字是倒序的，它还会将它们反转成正序。

private static <T> int countRunAndMakeAscending(T[] a, int lo, int hi, Comparator<? super T> c) {
    assert lo < hi;
    int runHi = lo + 1;
    if (runHi == hi)
        return 1;

    // 找到 run 的结束位置，并在降序情况下反转范围
    if (c.compare(a[runHi++], a[lo]) < 0) {  // 降序
        while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) < 0)
            runHi++;
        reverseRange(a, lo, runHi);
    } else {  // 升序
        while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) >= 0)
            runHi++;
    }

    return runHi - lo;
}

mergeCollapse : 将连续的有序小段合并成更大的有序段

mergeCollapse 的主要作用就是在排序过程中，将连续的有序小段合并成更大的有序段，以便更高效地进行排序。

/**
     * Examines the stack of runs waiting to be merged and merges adjacent runs
     * until the stack invariants are reestablished:
     * 检查等待合并的运行堆栈，并合并相邻的运行，直到满足堆栈条件：
     *     1. runLen[i - 3] > runLen[i - 2] + runLen[i - 1]
     *     2. runLen[i - 2] > runLen[i - 1]
     *
     * This method is called each time a new run is pushed onto the stack,
     * so the invariants are guaranteed to hold for i < stackSize upon
     * entry to the method.
     * 每次将新的运行推入堆栈时，都会调用此方法，因此在进入方法时，对于 i < stackSize，满足堆栈条件。
     */
 private void mergeCollapse() {
    while (stackSize > 1) {
        int n = stackSize - 2;
        if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) {
            if (runLen[n - 1] < runLen[n + 1])
                n--;
            // 在位置 n 处合并相邻的运行
            mergeAt(n);
        } else if (runLen[n] <= runLen[n + 1]) {
            // 在位置 n 处合并相邻的运行
            mergeAt(n);
        } else {
            // 堆栈条件已满足，退出循环
            break;
        }
    }
}

mergeAt(n) : 把两个有序的小段合并成一个更大的有序段

mergeAt(n) ：它帮助我们把两个有序的小段合并成一个更大的有序段，以便在排序过程中保持正确的顺序。

/**
 * Merges the two runs at stack indices i and i+1. Run i must be
 * the penultimate or antepenultimate run on the stack. In other words,
 * i must be equal to stackSize-2 or stackSize-3.
 *
 * @param i stack index of the first of the two runs to merge
 */
private void mergeAt(int i) {
    assert stackSize >= 2;
    assert i >= 0;
    assert i == stackSize - 2 || i == stackSize - 3;

    int base1 = runBase[i];
    int len1 = runLen[i];
    int base2 = runBase[i + 1];
    int len2 = runLen[i + 1];
    assert len1 > 0 && len2 > 0;
    assert base1 + len1 == base2;

    // 记录合并后的 run 长度；如果 i 是倒数第三个 run，也要滑动最后一个 run（不参与本次合并）
    runLen[i] = len1 + len2;
    if (i == stackSize - 3) {
        runBase[i + 1] = runBase[i + 2];
        runLen[i + 1] = runLen[i + 2];
    }
    stackSize--;

    // 找到 run2 中第一个元素在 run1 中的插入位置
    int k = gallopRight(a[base2], a, base1, len1, 0, c);
    assert k >= 0;
    base1 += k;
    len1 -= k;
    if (len1 == 0)
        return;

    // 找到 run1 中最后一个元素在 run2 中的插入位置
    len2 = gallopLeft(a[base1 + len1 - 1], a, base2, len2, len2 - 1, c);
    assert len2 >= 0;
    if (len2 == 0)
        return;

    // 使用临时数组（长度为 min(len1, len2)）合并剩余的 run
    if (len1 <= len2)
        mergeLo(base1, len1, base2, len2);
    else
        mergeHi(base1, len1, base2, len2);
}

gallopRigth && gallopLeft :在有序数组中快速查找目标元素的可能位置,便于合并

其中两个主要的方法就是gallopRigth()和gallopLeft() 。这里就是上面所说的 找元素的部分。

主要作用就是在有序数组中快速查找目标元素的可能位置，它采用一种跳跃式的查找策略，通过快速定位可能的位置，提高查找速度。
也就是上文中这一部分：

假设以下内容：
第一个段包含元素：[1,2,3,5,6,8,9]
第二个段包含元素：[4,6,7,8,10,11,12]

第一个段在数组中出现在第二个段之前。请注意，实际段落长度不会这么短。如前所述，段落长度应介于16到32之间。此处只是提供示例以说明问题。
gallopRight()：查找第二个段的第一个元素在第一个段中的位置。例如，在此示例中，位置为2。这意味着前两个元素不需要参与合并，它们的位置不需要改变。

gallopLeft()：查找第一个段的最后一个元素在第二个段中的位置。在此处，发现第二个段中的第四个元素为10。因此，第二个段中的10、11、12不需要参与合并，它们的位置也不需要改变。

这样参与合并的段的长度就大大减小，时间相应的就变短了（算法的优化点之一）。gallopLeft 代码如下：

gallopLeft 方法用于在有序数组的指定范围内进行快速查找，定位将指定键插入的位置或最左边相等元素的索引。它使用跳跃式的查找策略，根据键与范围内元素的比较结果，通过不断调整步长进行左跳或右跳，直到找到合适的插入位置。最后，使用二分查找在找到的范围内确定确切的插入位置，并返回结果。这个方法的目标是提高查找效率。

/**
 * Locates the position at which to insert the specified key into the
 * specified sorted range; if the range contains an element equal to key,
 * returns the index of the leftmost equal element.
 *
 * @param key 要搜索插入位置的键
 * @param a 要搜索的数组
 * @param base 范围内第一个元素的索引
 * @param len 范围的长度；必须大于 0
 * @param hint 开始搜索的索引，0 <= hint < n。hint 越接近结果，该方法的执行速度越快。
 * @param c 用于对范围进行排序和搜索的比较器
 * @return 整数 k，0 <= k <= n，满足 a[b + k - 1] < key <= a[b + k]，
 *    假设 a[b - 1] 是负无穷大，a[b + n] 是正无穷大。
 *    换句话说，键属于索引 b + k 处；或者换句话说，
 *    数组 a 的前 k 个元素应该在键之前，后面的 n - k 个元素应该在键之后。
 */
private static <T> int gallopLeft(T key, T[] a, int base, int len, int hint,
                                  Comparator<? super T> c) {
    assert len > 0 && hint >= 0 && hint < len;
    int lastOfs = 0;
    int ofs = 1;
    if (c.compare(key, a[base + hint]) > 0) {
        // 向右跳跃，直到 a[base+hint+lastOfs] < key <= a[base+hint+ofs]
        int maxOfs = len - hint;
        while (ofs < maxOfs && c.compare(key, a[base + hint + ofs]) > 0) {
            lastOfs = ofs;
            ofs = (ofs << 1) + 1;
            if (ofs <= 0)   // 检查 int 溢出
                ofs = maxOfs;
        }
        if (ofs > maxOfs)
            ofs = maxOfs;

        // 将偏移量相对于基准位置进行调整
        lastOfs += hint;
        ofs += hint;
    } else { // key <= a[base + hint]
        // 向左跳跃，直到 a[base+hint-ofs] < key <= a[base+hint-lastOfs]
        final int maxOfs = hint + 1;
        while (ofs < maxOfs && c.compare(key, a[base + hint - ofs]) <= 0) {
            lastOfs = ofs;
            ofs = (ofs << 1) + 1;
            if (ofs <= 0)   // 检查 int 溢出
                ofs = maxOfs;
        }
        if (ofs > maxOfs)
            ofs = maxOfs;

        // 将偏移量相对于基准位置进行调整
        int tmp = lastOfs;
        lastOfs = hint - ofs;
        ofs = hint - tmp;
    }
    assert -1 <= lastOfs && lastOfs < ofs && ofs <= len;

    /*
     * 现在 a[base+lastOfs] < key <= a[base+ofs]，
     * 因此键位于 lastOfs 的右侧，但不超过 ofs 的位置。
     * 使用二分查找，在不变式 a[base + lastOfs - 1] < key <= a[base + ofs] 的条件下进行。
     */
    lastOfs++;
    while (lastOfs < ofs) {
        int m = lastOfs + ((ofs - lastOfs) >>> 1);

        if (c.compare(key, a[base + m]) > 0)
            lastOfs = m + 1;  // a[base + m] < key
        else
            ofs = m;          // key <= a[base + m]
    }
    assert lastOfs == ofs;    // 所以 a[base + ofs - 1] < key <= a[base + ofs]
    return ofs;
}

TimSort 算法的优缺点

优点

1. 稳定性：TimSort 是一种稳定的排序算法，即相等元素的相对顺序在排序后保持不变。
2. 高效的处理小规模或部分有序数组：TimSort 在处理小规模数组时具有良好的性能，可以利用插入排序的优势。此外，对于部分有序的数组，TimSort 也能快速识别并进行优化处理。
3. 最坏情况下的时间复杂度是 O(n log n)：在最坏情况下，TimSort 的时间复杂度与其他基于比较的排序算法（如快速排序和归并排序）相同，都是 O(n log n)。
4. 适用于大多数实际数据：TimSort 是一种自适应的排序算法，它能够根据输入数据的特性进行优化，适应不同的数据分布和大小。

缺点

1. 需要额外的空间：TimSort 在合并阶段需要额外的辅助空间，用于暂存部分数组。这可能导致空间复杂度较高，特别是对于大规模数据排序时。
2. 对于某些特殊情况效率较低：在处理某些特殊情况下，例如完全逆序的数组。

最后：

通过查看 TimSort 的源码，可以深入了解该算法的工作原理、核心步骤和关键逻辑。这有助于我们对排查问题时快速丁文问题，也有助于对算法的理解和知识的扩展。

另外 TimSort 是一种经过优化的排序算法，它采用了多种技巧来提高性能和效率。通过研究源码，我们可以学习到一些优化技巧，例如插入、二分查找的优化、自适应调整等。这些技巧或许可以用在我们日后的开发场景中。当然，最重要的还是去逐渐体会、借鉴其实现方式和设计优化思想。

---

最后的最后，谢谢小明。
小明：

参考：

排序算法——Timsort

java8中List中sort方法解析