文章目录
- 欧拉函数
- 线性筛求欧拉函数
- 欧拉定理
- 快速幂
- 逆元
- 扩展欧几里得
- 中国剩余定理
- 扩展中国剩余定理
- 欧拉函数练习题
- 873. 欧拉函数
- 874. 筛法求欧拉函数
- 快速幂练习题
- 875. 快速幂
- 876. 快速幂求逆元
- 扩展欧练习题
- 877. 扩展欧几里得算法
- 878. 线性同余方程
- 中国剩余定理练习题
- 204. 表达整数的奇怪方式
脑阔疼
欧拉函数
互质:若N个整数的最大公约数是1,那么称这N个数互质
公式:

思路是容斥原理:
如何求1~N中和N互质的数的个数?现有质数
p
1
p_1
p1,
p
2
p_2
p2, … ,
p
k
p_k
pk < N
- 从1~N中删除 p 1 p_1 p1, p 2 p_2 p2, … , p k p_k pk 的所有倍数(不包括质数本身)
- 加上两个质数相乘的倍数
- 删除三个质数相乘的倍数
- 加上四个质数相乘的倍数
- …不断重复
为什么会不断重复?因为删除
p
1
p_1
p1,
p
2
p_2
p2, … ,
p
k
p_k
pk 的所有倍数时,可能有的数(
p
i
p_i
pi与
p
j
p_j
pj的倍数)被二次删除,导致最终得到的结果变小,所以需要加上被二次删除的数
加上被二次删除的数后,又有些数(
p
i
p_i
pi,
p
j
p_j
pj与
p
k
p_k
pk的倍数)被二次加上,需要删除这些数
删除被二次加上的时后,又有些数(
p
i
p_i
pi,
p
j
p_j
pj,
p
k
p_k
pk与
p
l
p_l
pl的倍数)被二次删除,需要加上这些数
…不断重复,重复加减k次就能求得欧拉数
N
−
N
p
1
−
N
p
2
.
.
.
−
N
p
k
+
N
p
1
p
2
+
.
.
.
+
(
−
1
n
−
1
)
N
p
1
p
2
.
.
.
p
k
N-\frac{N}{p_1}-\frac{N}{p_2}...-\frac{N}{p_k}+\frac{N}{p_1p_2}+...+(-1^{n-1})\frac{N}{p_1p_2...p_k}
N−p1N−p2N...−pkN+p1p2N+...+(−1n−1)p1p2...pkN
公式类似这样,不断的加减直到分母由k个质数相乘为止
同时公式能够整理成y总板书中的那种格式:
ϕ
(
N
)
=
N
(
1
−
1
p
1
)
(
1
−
1
p
2
)
(
1
−
1
p
3
)
.
.
.
(
1
−
1
p
k
)
ϕ(N)=N(1-\frac{1}{p_1})(1-\frac{1}{p_2})(1-\frac{1}{p_3})...(1-\frac{1}{p_k})
ϕ(N)=N(1−p11)(1−p21)(1−p31)...(1−pk1)
或者是这种格式:
ϕ
(
N
)
=
N
(
p
1
−
1
p
1
)
(
p
2
−
1
p
2
)
(
p
3
−
1
p
3
)
.
.
.
(
p
k
−
1
p
k
)
ϕ(N)=N(\frac{p_1-1}{p_1})(\frac{p_2-1}{p_2})(\frac{p_3-1}{p_3})...(\frac{p_k-1}{p_k})
ϕ(N)=N(p1p1−1)(p2p2−1)(p3p3−1)...(pkpk−1)
模板:分解质因数的板子,找到质因数后根据公式进行运算即可
int phi(int n)
{
int res = n;
for (int i = 2; i <= n / i; ++ i )
{
if (n % i == 0)
{
res = res / i * (i - 1);
while (n % i == 0) n /= i;
}
}
if (n > 1) res = res / n * (n - 1);
return res;
}
线性筛求欧拉函数
定义ϕ为欧拉函数,若n是质数,那么ϕ(n) = n - 1,因为2~n-1中没有数能整除n,同时1和n互质,所以1~n-1的所有数都与n互质,即ϕ(n) = n - 1
若要求某个范围内所有数的欧拉数,可以套用线性筛的板子,若当前数是质数,那么ϕ(n) = n - 1
若当前数是合数,在线性筛中分两种情况:用i遍历1~n的所有数,用j遍历当前已经找出的质数
i % primes[j] == 0,说明此时枚举的质数是该合数的最小质因子,而i * primes[j]的最小质因子也是primes[j]。此时的ϕ(i * primes[j])比ϕ(i)多乘了primes[j],所以ϕ(i * primes[j]) = ϕ(i) * primes[j]i % primes[j] != 0,说明此时枚举的质数小于该合数的最小质因子,i * primes[j]的最小质因子为primes[j],此时的ϕ(i * primes[j])比ϕ(i)多乘了primes[j]与(1 - 1/primes[j])。所以此时的ϕ(i * primes[j]) = primes[j] * ϕ(i) * (1 - 1/primes[j]),化简后就是ϕ(i * primes[j]) = ϕ(i) * (primes[j] - 1)
模板:
int eulers[N], primes[N], cnt;
bool st[N];
void get_eulers(int n)
{
eulers[1] = 1;
for (int i = 1; i <= n; ++ i )
{
if (!st[i]) primes[cnt ++ ] = i, eulers[i] = i - 1;
for (int j = 0; primes[j] < n / i; ++ j )
{
int t = i * primes[j];
st[t] = true;
if (i % primes[j] == 0)
{
eulers[t] = primes[j] * eulers[i];
break;
}
eulers[t] = eulers[i] * (eulers[i] - 1);
}
}
}
欧拉定理
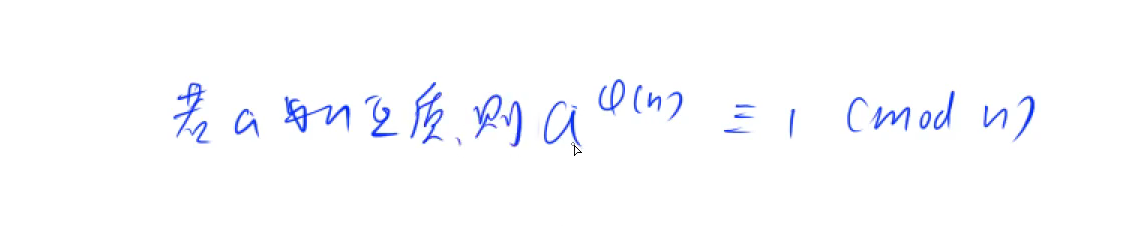
先说明一个简单的性质:如果ac≡bc(mod m),并且c和m互质,则a≡b(mod m)
证明:
首先,当a = b或者c = 1时,a≡b(mod m)成立
当a > b并且c ≠ 1时,ac ≡bc(mod m)等价于ac = bc + km
整理得:c(a - b) = km,a - b = km / c
因为a - b是正整数,并且c和m互质,即m / c一定不为整数
所以k / c一定为整数,即a = b + k’m,等价于a ≡ b (mod m)
证明完毕,举个反例,当a = 2, b = 4, c = 2, m = 4时,c和m不互质
此时2 * 2 ≡ 2 * 4 (mod 4),两边同除2
2 ≡ 4 (mod 4)显然不成立
总之:记住这个结论,很常用。c和m互质的情况下,不论是两边同乘c还是同除c都是成立的
证明欧拉定理:
a
a
a与
n
n
n互斥,1~n中,与
n
n
n互质的数有
a
1
a_1
a1,
a
2
a_2
a2, … ,
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)
a
a
a与
n
n
n互斥并且
a
i
a_i
ai与
n
n
n互质
所以
a
a
a *
a
1
a_1
a1,
a
a
a *
a
2
a_2
a2, … ,
a
a
a *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)也是与n互质的
现证明
a
a
a *
a
i
a_i
ai与
a
a
a *
a
j
a_j
aj不相同,即
a
a
a *
a
1
a_1
a1,
a
a
a *
a
2
a_2
a2, … ,
a
a
a *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)两两不同
用反证法:假设
a
a
a *
a
i
a_i
ai与
a
a
a *
a
j
a_j
aj相同,那么有
a
a
a *
a
i
a_i
ai ≡
a
a
a *
a
j
a_j
aj (mod n)
因为
a
a
a与
n
n
n互质,所以
a
i
a_i
ai ≡
a
j
a_j
aj (mod n),与前提
a
1
a_1
a1,
a
2
a_2
a2, … ,
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)是1~n中与n互质的数矛盾
所以
a
a
a *
a
1
a_1
a1,
a
a
a *
a
2
a_2
a2, … ,
a
a
a *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)中,不存在相同的两个数
即
a
a
a *
a
1
a_1
a1,
a
a
a *
a
2
a_2
a2, … ,
a
a
a *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)是互不相同且与n互质的数
因为
a
1
a_1
a1,
a
2
a_2
a2, … ,
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)也是互不相同且与n互质的数
所以
a
1
a_1
a1 *
a
2
a_2
a2 * … *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n) ≡
a
a
a *
a
1
a_1
a1,
a
a
a *
a
2
a_2
a2, … ,
a
a
a *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n) (mod n)
整理得
a
1
a_1
a1 *
a
2
a_2
a2 * … *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n) ≡
a
ϕ
(
n
)
a^ {ϕ(n)}
aϕ(n) *
a
1
a_1
a1, *
a
2
a_2
a2 * … *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n) (mod n)
由于
a
i
a_i
ai与n互质,所以两边同除
a
1
a_1
a1 *
a
2
a_2
a2 * … *
a
ϕ
(
n
)
a_{ϕ(n)}
aϕ(n)
得到
a
ϕ
(
n
)
a^ {ϕ(n)}
aϕ(n) ≡ 1 (mod n)
证明完毕
注意欧拉定理的前提是a与n互质
特别的当n为质数时,有结论:
a
n
−
1
a^ {n-1}
an−1 ≡ 1 (mod n)
这是费马小定理
快速幂
在O(logk) 的时间复杂度下,快速地求出 a k a^k ak % p的结果
计算n每个因子%p的结果,然后将这些结果相乘再%p,得到的结果和n % p相同
预处理:将
a
k
a^k
ak分解成
a
2
i
a^{2^i}
a2i,也就是将k拆分成多个
2
i
2^i
2i,其中i范围为:0~logk
当i等于logk时,
2
i
2^i
2i = k。我们需要选择一些
2
i
2^i
2i,使它们相加等于k
也就是k的二进制表示中,1在哪一位上,i就是几
比如k = 5,5的二进制表示101,那么5就可以拆分成:
2
0
2^0
20 +
2
2
2^2
22
k
k
k作为
a
a
a的指数,那么
a
a
a的
k
k
k次方就可以根据k的拆分,被拆分成多个式子相乘(最多32或64个式子)
比如
a
5
a^5
a5 被拆分成
a
2
0
a^{2^0}
a20 *
a
2
2
a^{2^2}
a22,要求
a
k
a^k
ak %
p
p
p,可以将
a
k
a^k
ak进行拆分,将拆分后每个式子%
p
p
p的结果相乘,最后再%
p
p
p即可
如何用代码实现?
k的二进制表示中,有几个1,
a
k
a^k
ak就能被拆分成几个式子相乘
当k的第i位为1,表示式子
a
2
i
a^{2^i}
a2i需要累乘
我们不断右移k,同时让a不断自乘(
a
1
a^1
a1,
a
2
a^2
a2,
a
4
a^4
a4,
a
8
a^8
a8…)。当k的第i位为1,直接* a % p
模板:
int qmi(int a, int k, int p)
{
lont lont res = 1;
while (k)
{
if (k & 1) res = res * a % p;
a = (long long)a * a % p;
k >>= 1;
}
return res;
}
逆元
在数论问题中,我们不希望进行除法运算,因为除法可能得到小数,处理小数很麻烦
我们希望进行乘法运算,乘法运算只会得到整数,处理整数是很方便的
所以当一个数作为除数参数运算时,我们希望它能作为一个乘数参与运算
对于一个除数b,若存在一个整数x,使得用x做乘法运算的结果,与原除法运算结果相同,那么x就是b的乘法逆元。可以用以下式子表示:
a / b ≡ a * x (mod m)
注意:这里运算的结果需要取模m,结果相同也意味着运算并取模m后的结果相同,乘法逆元更准确的叫法是模m乘法逆元
b
b
b的模m乘法逆元用
b
−
1
b^{-1}
b−1表示,需要与
b
b
b的逆做区分
整理式子:
a
/
b
≡
a
∗
x
(
m
o
d
m
)
a / b ≡ a * x (mod\ m)
a/b≡a∗x(mod m)
两边同乘
b
b
b得到
a
≡
b
∗
a
∗
b
−
1
(
m
o
d
m
)
a ≡ b * a * b^{-1} (mod\ m)
a≡b∗a∗b−1(mod m)
式子两边同除
a
a
a得到:
b
∗
b
−
1
≡
1
(
m
o
d
m
)
b * b^{-1} ≡ 1(mod\ m)
b∗b−1≡1(mod m)
当m是质数时,根据费马定理:
b
m
−
1
≡
1
(
m
o
d
m
)
b^{m - 1} ≡ 1 (mod\ m)
bm−1≡1(mod m)
整理得:
b
∗
b
m
−
2
≡
1
(
m
o
d
m
)
b * b^{m - 2} ≡ 1 (mod\ m)
b∗bm−2≡1(mod m)
经过对比,在m质数的情况下,我们要求的
b
−
1
b^{-1}
b−1等价于
b
m
−
2
b^{m -2}
bm−2
综上,
b
b
b的模m乘法逆元为
b
m
−
2
b^{m -2}
bm−2,已知
b
b
b和
m
m
m即可直接求出逆元
所以求逆元的本质就是快速幂,板子和快速幂一样,参数为qmi(b, m - 2, m)
扩展欧几里得
裴蜀定理:对于任意整数(a, b)一定存在非零整数(x, y)使得
ax + by = d,其中d是(a, b)的最大公约数
裴蜀定理证明:(a, b)的最大公约数d能够整除a与b,可知d | ax + by。假设ax + by = D,那么D就能被d整除,将式子乘以d/D,就能得到a'x + b'y = d
即存在非零整数a’与b’使得a'x + b'y = d,证明完毕
扩展欧几里得:求解系数
(x, y)使得式子ax + by = d成立,其中d是(a, b)的最大公约数
用(a, b)表示a与b的最大公约数,在欧几里得算法中,我们证明过(a, b) = (b, a % b)
若等式ax + by = d (1)成立,那么等式(a % b)x' + by' = d也会成立,整理等式使两式格式相同:
(
a
−
[
a
/
b
]
b
)
x
′
+
b
y
′
=
d
(a - [a/b]b) x' + by' = d
(a−[a/b]b)x′+by′=d
整理a与b的系数:
a
x
′
+
b
(
y
′
−
[
a
/
b
]
x
′
)
=
d
(
2
)
ax'+b(y'-[a/b]x')=d\ (2)
ax′+b(y′−[a/b]x′)=d (2)
对比(1)式与(2)式,要使两式相同,那么(2)式中a的系数x' = x,b的系数y' - [a/b]x' = y
也就是说,若我们知道系数(x', y')使式子(a % b)x' + by' = d成立,那么我们就能求得系数(x, y)使得式子ax + by = d成立
在欧几里得算法中,我们通过递归使得(a, b)中的b不断地接近0,当b为0时,向下递归结束,程序将向上递归
若b = 0,此时使式子ax + by = d成立的(x, y)的值为(1, 0)
带入递归过程,每一次向下递归都是将(a. b)转换成(b, a % b)
在裴蜀定理中,a和b的转换导致了其系数(x, y)向(x', y')的转换,现已知最终的系数(1, 0)
它是一次递归过程中的(x', y'),我们可以推导出该递归过程中的(x, y)
然后将其作为上一个递归过程的(x', y'),不断地向上递归,直到推导出首个递归过程的(x, y),此时求解完成
模板:
// 函数返回最大公约数,扩展欧的系数(x, y)通过输出型参数返回
int exgcd(int a, int b, int& x, int& y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
中国剩余定理
给定一组互质的数
m
i
m_i
mi,和数量相同的另一组数
a
i
a_i
ai,可以构造出x,使x与
m
i
m_i
mi互质并且满足以下线性方程组

x在模
m
i
m_i
mi的情况下是唯一的
首先M表示所有
m
i
m_i
mi的乘积,
M
i
M_i
Mi表示M /
m
i
m_i
mi
那么有通解:
x
=
a
1
M
1
M
1
−
1
+
a
2
M
2
M
2
−
1
+
.
.
.
+
a
k
M
k
M
k
−
1
x = a_1M_1M_1^{-1}+a_2M_2M_2^{-1}+...+a_kM_kM_k^{-1}
x=a1M1M1−1+a2M2M2−1+...+akMkMk−1
来看为什么这个通解成立,在mod
m
1
m_1
m1的情况下,只有
M
1
M_1
M1
M
1
−
1
M_1^{-1}
M1−1 = 1,
M
i
M_i
Mi
M
i
−
1
M_i^{-1}
Mi−1 = 0
因为
M
i
M_i
Mi中含有因子
m
1
m_1
m1,所以
m
1
m_1
m1能够整除
M
i
M_i
Mi
扩展中国剩余定理

中国剩余定理用于解决一组互质模同余方程问题
而扩展中国剩余定理用于解决一组不互质模同余方程问题,即
m
i
m_i
mi之间不互质
同余方程的形式是:
x
≡
a
i
(
m
o
d
m
i
)
x ≡ a_i (mod\ m_i)
x≡ai(mod mi)
变形一下有:
x
=
a
i
+
k
m
i
x = a_i+ k m_i
x=ai+kmi
同时x要满足另一同余方程:x =
a
j
a_j
aj + k *
m
j
m_j
mj,联立两式可以得到:
a
i
+
k
i
m
i
=
a
j
+
k
j
m
j
a_i + k_im_i = a_j + k_jm_j
ai+kimi=aj+kjmj
整理得:
k
i
m
i
−
k
j
m
j
=
a
j
−
a
i
k_im_i - k_jm_j= a_j - a_i
kimi−kjmj=aj−ai
这个式子可以用扩展欧求解,假设(a, b)的最大公约数为d
(
m
i
m_i
mi,
m
j
m_j
mj)对应(a, b),(
k
i
k_i
ki,
k
j
k_j
kj)对应(a, b)的系数(x, y),若(
a
j
a_j
aj -
a
i
a_i
ai )是d的倍数,那么(
k
i
k_i
ki,
k
j
k_j
kj)有解
否则无解
求出一对特解后,令
k
i
=
k
i
+
m
j
d
k
,
k
j
=
k
j
+
m
i
d
k
(
k
=
.
.
.
,
−
2
,
−
1
,
0
,
1
,
2
,
.
.
.
)
k_i = k_i+\frac{m_j}{d}k,\ k_j = k_j+\frac{m_i}{d}k\ (k = ...,-2,-1,0, 1, 2,...)
ki=ki+dmjk, kj=kj+dmik (k=...,−2,−1,0,1,2,...)
通过特解就能求出通解(将通解带入等式
a
i
a_i
ai +
k
i
k_i
ki *
m
i
m_i
mi =
a
j
a_j
aj +
k
j
k_j
kj *
m
j
m_j
mj,等式依然成立)
为什么
m
i
m_i
mi与
m
j
m_j
mj要除以d?为了保证此时计算出的特解互质,以提高求出完整特解的速度
回到一开始的式子:x =
a
i
a_i
ai +
k
i
k_i
ki *
m
i
m_i
mi,计算出通解后将通解带入式子
x
=
a
i
+
(
k
i
+
m
j
d
k
)
m
i
x=a_i + (k_i+\frac{m_j}{d}k)m_i
x=ai+(ki+dmjk)mi
展开得到:
x
=
a
i
+
k
i
m
i
+
m
i
m
j
d
k
x=a_i + k_im_i+\frac{m_im_j}{d}k
x=ai+kimi+dmimjk
再证明一个常用的性质:gcd(a, b) * lcm(a, b) = a * b
a与b的最大公约数与最小公倍数的乘积等于a与b的乘积
使用分解质因数法证明:
假设最大公约数为d,最小公倍数为m
将a和b质因数分解:a = d * p1* p2 * ... * pr, b = d * q1 * q2 * ... * qs
其中d是a和b中相同的质因数,也就是最小公约数
那么m就是所有质因数的乘积m = d * p1* p2 * ... * pr * q1 * q2 * ... * qs
那么ab = dm
证明完毕
所以
m
i
m_i
mi
m
j
m_j
mj/d = m,m为
m
i
m_i
mi和
m
j
m_j
mj最小公倍数,等式为:
x
=
a
i
+
k
i
m
i
+
k
m
(
k
=
.
.
.
,
−
2
,
−
1
,
0
,
1
,
2...
)
x=a_i + k_im_i+km\ (k = ...,-2,-1,0, 1, 2...)
x=ai+kimi+km (k=...,−2,−1,0,1,2...)
其中
a
i
a_i
ai和
k
i
k_i
ki
m
i
m_i
mi是已知的数,可以将整个式子看成
x
=
c
+
k
m
x = c + km
x=c+km
也就是x ≡ c (mod m)
最终要求的是最小非负整数x,转换这个式子:
x
=
k
1
m
+
c
′
x = k_1m + c'
x=k1m+c′
对于c,有:
c
=
k
2
m
+
c
′
c=k_2m+c'
c=k2m+c′
两式的c’在m的剩余系中,并且c’相同,只有
k
1
k_1
k1和
k
2
k_2
k2不同,根据c’合并两式
c
=
k
2
m
+
(
x
−
k
1
m
)
c=k_2m+(x-k_1m)
c=k2m+(x−k1m)
整理得:
c
=
(
k
2
−
k
1
)
m
+
x
c=(k_2-k_1)m+x
c=(k2−k1)m+x
可以看成c ≡ x (mod m),要求最小非负整数,x就要在m的剩余系中,所以x = c mod m
而c =
k
i
k_i
ki
m
i
m_i
mi +
a
i
a_i
ai,
a
i
a_i
ai和
m
i
m_i
mi已知,
k
i
k_i
ki根据扩展欧求得,所以c是已知的,m是(
m
i
m_i
mi,
m
j
m_j
mj)的最小公倍数,根据扩展欧也能求得。所以x = c mod m中,只有x未知,其他参数已知,那么x就能被求出,最终求x的式子是:
x
=
c
m
o
d
m
x = c\ mod\ m
x=c mod m
但是这个x只是满足两个线性同余方程的通解,要让x满足所有线性同余方程,就要重复上面的步骤(n - 1)次(假设方程有n个)。重复操作如何进行?对某两个线性同余方程求出通解后,有式子:
x
=
a
i
+
k
i
m
i
+
k
m
(
k
=
.
.
.
,
−
2
,
−
1
,
0
,
1
,
2...
)
x=a_i + k_im_i+km\ (k = ...,-2,-1,0, 1, 2...)
x=ai+kimi+km (k=...,−2,−1,0,1,2...)
而第i个线性同余方程是:
x
=
k
i
m
i
+
a
i
x=k_im_i+a_i
x=kimi+ai
将通解中的
a
i
a_i
ai+
k
i
k_i
ki
m
i
m_i
mi作为新的
a
i
a_i
ai,
m
m
m作为新的
m
i
m_i
mi,得到一个新的线性同余方程,将其与第k个线性同余方程联立,重复以上所有操作,求出满足两式的非负最小x
用于每次联立两式求出的x满足非负最小,重复n - 1求出的x也满足非负最小,局部最优推出全局最优,所以一定能保证对于所有的方程来说,x是非负最小的
总结下:通过扩展欧求特解,通过特解求通解,通过通解求x,重复n - 1次
模板:
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
LL ai, aj, mi, mj, ki, kj;
LL x = 0;
int n;
scanf("%d", &n);
scanf("%ld%ld", &mi, &ai);
for (int i = 0; i < n - 1; ++ i )
{
scanf("%ld%ld", &mj, &aj);
LL d = exgcd(mi, mj, ki, kj);
if ((aj - ai) % d)
{
x = -1;
break;
}
ki = (aj - ai) / d * ki;
LL t = mj / d;
ki = (ki % t + t) % t;
// 用通解更新ai和mi,使两式合并
ai = ai + ki * mi;
mi = mi / d * mj;
}
if (x != -1) x = (ai % mi + mi) % mi;
printf("%ld\n", x);
欧拉函数练习题
873. 欧拉函数
873. 欧拉函数 - AcWing题库
#include <iostream>
using namespace std;
int n;
int phi(int x)
{
int res = x;
for (int i = 2; i <= x / i; ++ i )
{
if (x % i == 0)
{
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
}
if (x > 1) res = res / x * (x - 1);
return res;
}
int main()
{
scanf("%d", &n);
int x;
while (n -- )
{
scanf("%d", &x);
printf("%d\n", phi(x));
}
return 0;
}
874. 筛法求欧拉函数
874. 筛法求欧拉函数 - AcWing题库

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int cnt, primes[N], eulers[N];
bool st[N];
int n;
void get_eulers(int n)
{
eulers[1] = 1;
for (int i = 2; i <= n; ++ i )
{
if (!st[i]) primes[cnt ++ ] = i, eulers[i] = i - 1;
for (int j = 0; primes[j] <= n / i; ++ j )
{
int t = i * primes[j];
st[t] = true;
if (i % primes[j] == 0)
{
eulers[t] = eulers[i] * primes[j];
break;
}
eulers[t] = eulers[i] * (primes[j] - 1);
}
}
}
int main()
{
scanf("%d", &n);
get_eulers(n);
long long res = 0;
for (int i = 1; i <= n; ++ i) res += eulers[i];
printf("%ld\n", res);
return 0;
}
快速幂练习题
875. 快速幂
875. 快速幂 - AcWing题库
#include <iostream>
using namespace std;
typedef long long LL;
int n;
int qmi(int a, int k, int p)
{
LL res = 1;
while (k)
{
if (k & 1) res = res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
scanf("%d", &n);
int a, k ,p;
while (n -- )
{
scanf("%d%d%d", &a, &k, &p);
printf("%d\n", qmi(a, k, p));
}
return 0;
}
876. 快速幂求逆元
876. 快速幂求逆元 - AcWing题库

需要注意的是:题目保证p是一个质数,所以当a为p的倍数时,无法使用费马定理,逆元也就不存在
#include <iostream>
using namespace std;
typedef long long LL;
int n;
int qmi(int a, int k, int p)
{
LL res = 1;
while (k)
{
if (k & 1) res = res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
scanf("%d", &n);
int a, p;
while (n -- )
{
scanf("%d%d", &a, &p);
if (a % p == 0) puts("impossible");
else printf("%d\n", qmi(a, p - 2, p));
}
return 0;
}
扩展欧练习题
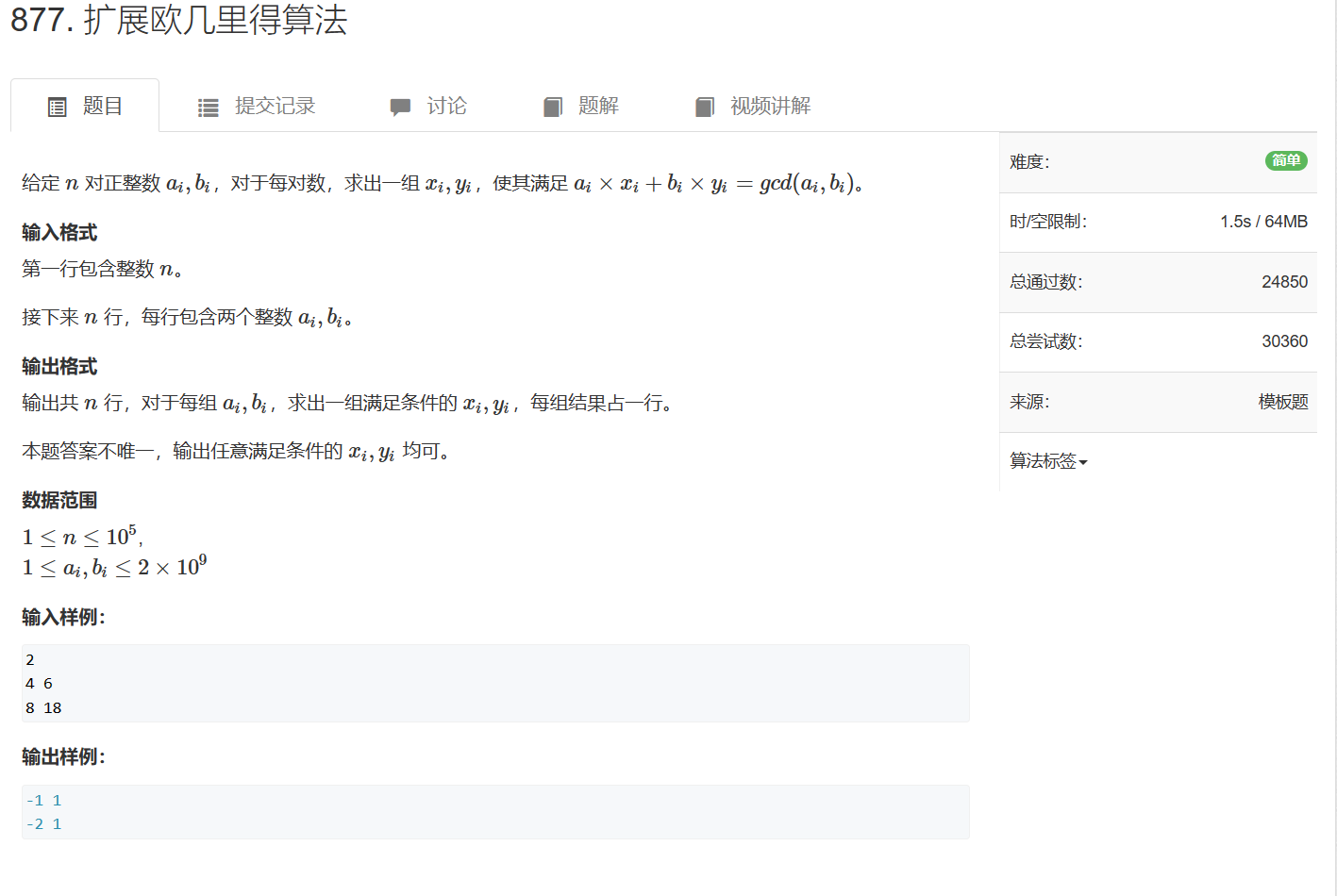
877. 扩展欧几里得算法
877. 扩展欧几里得算法 - AcWing题库
#include <iostream>
using namespace std;
int n;
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
scanf("%d", &n);
int a, b, x, y;
while (n -- )
{
scanf("%d%d", &a, &b);
exgcd(a, b, x, y);
printf("%d %d\n", x, y);
}
return 0;
}
878. 线性同余方程
878. 线性同余方程 - AcWing题库

等式ax ≡ b (mod m),当b <= m时,等式可以变形成ax = b + my,令y' = y,整理得ax + my' = b,题目给定a, m b,要求a的系数x
利用扩展欧可以求解两个系数x, y',不过使用扩展欧的前提是ax + my' = b,其中的b需要是(a, m)的最大公约数的倍数
也就是扩展欧需要先满足裴蜀定理,当b % (a, m) != 0时,扩展欧无法使用,等式无解
#include <iostream>
using namespace std;
typedef long long LL;
int n;
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
scanf("%d", &n);
int a, m, b, x, y, d;
while (n -- )
{
scanf("%d%d%d", &a, &b, &m);
d = exgcd(a, m, x, y);
if (b % d) puts("impossible");
else printf("%d\n", (LL)b / d * x % m);
}
return 0;
}
debug:在b % d != 0的情况下,ax + my = b与ax' + my' = d也是倍数关系,题目要返回的是x,而我们只求得x’,所以需要进行转换,输出b / d * x
不能输出x / d * b,因为x与d可能不是倍数关系,这样计算的结果将出现偏差
或者输出x * b / d也行,不过要注意long long的强转,防止爆int
最后需要保证答案在mod m剩余系中,所以要mod m
中国剩余定理练习题
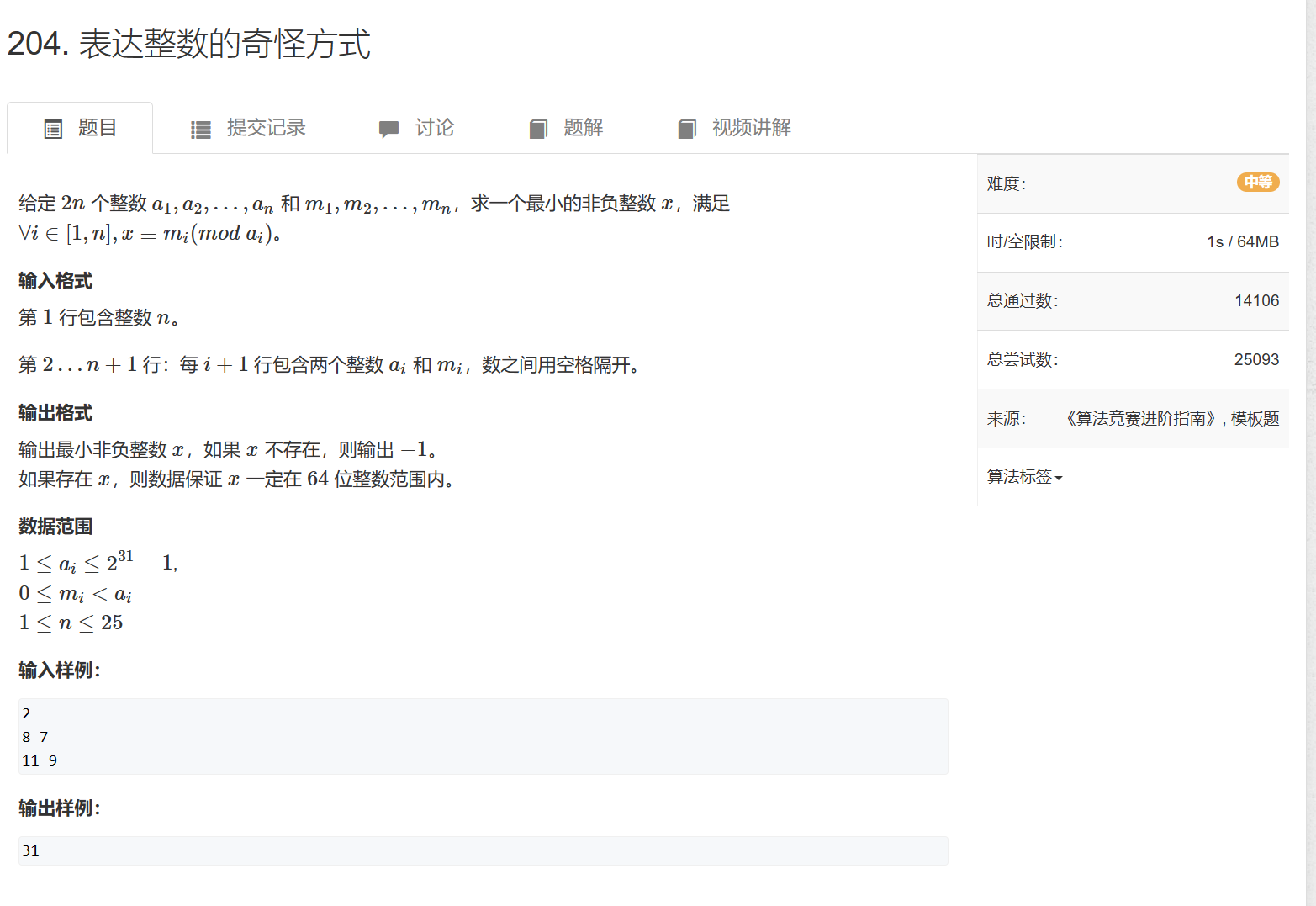
204. 表达整数的奇怪方式
204. 表达整数的奇怪方式 - AcWing题库
#include <iostream>
using namespace std;
typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
int main()
{
LL ai, aj, mi, mj, ki, kj;
LL x = 0;
int n;
scanf("%d", &n);
scanf("%ld%ld", &mi, &ai);
for (int i = 0; i < n - 1; ++ i )
{
scanf("%ld%ld", &mj, &aj);
LL d = exgcd(mi, mj, ki, kj);
if ((aj - ai) % d)
{
x = -1;
break;
}
ki = (aj - ai) / d * ki;
LL t = mj / d;
ki = (ki % t + t) % t;
// 用通解更新ai和mi,使两式合并
ai = ai + ki * mi;
mi = mi / d * mj;
}
if (x != -1) x = (ai % mi + mi) % mi;
printf("%ld\n", x);
return 0;
}