【题目来源】
https://www.luogu.com.cn/problem/P5018
https://www.acwing.com/problem/content/478/

【题目描述】
一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：
1.二叉树；
2.将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。
下图中节点内的数字为权值，节点外的 id 表示节点编号。

备注：图片来源于洛谷 https://www.luogu.com.cn/problem/P5018

现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数最多。请输出这棵子树的节点数。
注意：只有树根的树也是对称二叉树。本题中约定，以节点 T 为子树根的一棵“子树”指的是：节点T和它的全部后代节点构成的二叉树。

【输入格式】
第一行一个正整数 n，表示给定的树的节点的数目，规定节点编号1∼n，其中节点 1 是树根。
第二行 n 个正整数，用一个空格分隔，第 i 个正整数 vi 代表节点 i 的权值。
接下来 n 行，每行两个正整数 li,ri，分别表示节点 i 的左右孩子的编号。如果不存在左/右孩子，则以 −1 表示。两个数之间用一个空格隔开。

【输出格式】
输出文件共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

【数据范围】
vi≤1000,n≤10^6

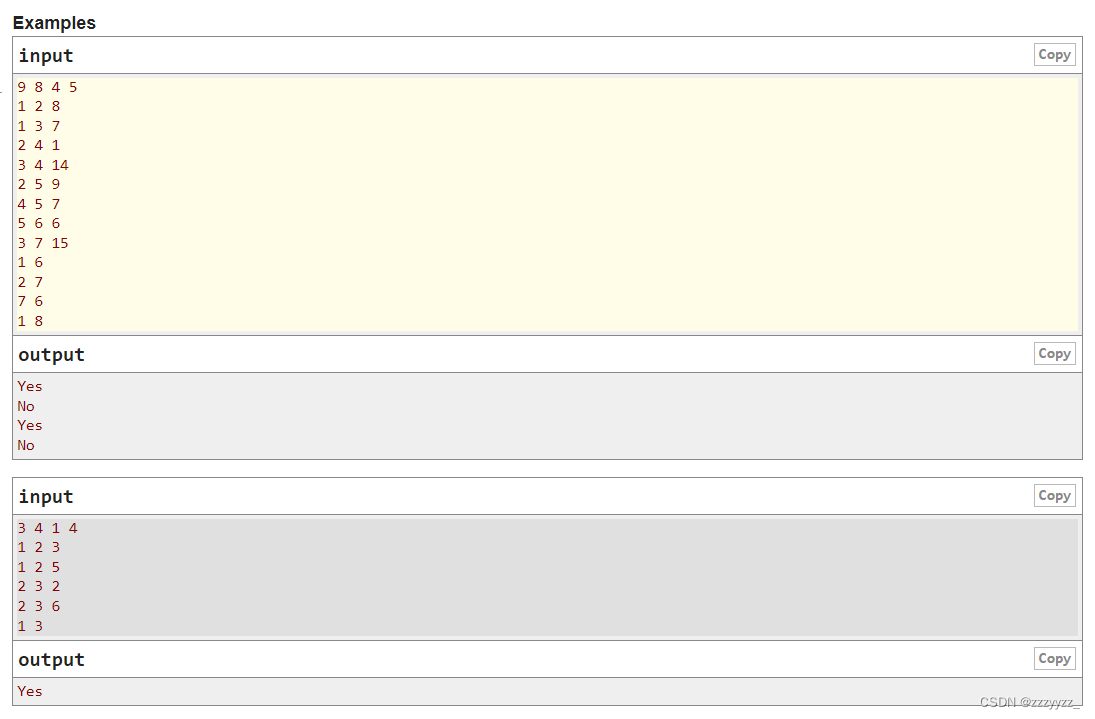
【输入输出样例】

input:
10 
2 2 5 5 5 5 4 4 2 3 
9 10 
-1 -1 
-1 -1 
-1 -1 
-1 -1 
-1 2 
3 4 
5 6 
-1 -1 
7 8

output:
3

【样例解析】
根据上述样例所得的二叉树如下所示。可知最大的对称二叉子树为以节点 7 为树根的子树，节点数为 3。

 备注：图片来源于洛谷 https://www.luogu.com.cn/problem/P5018

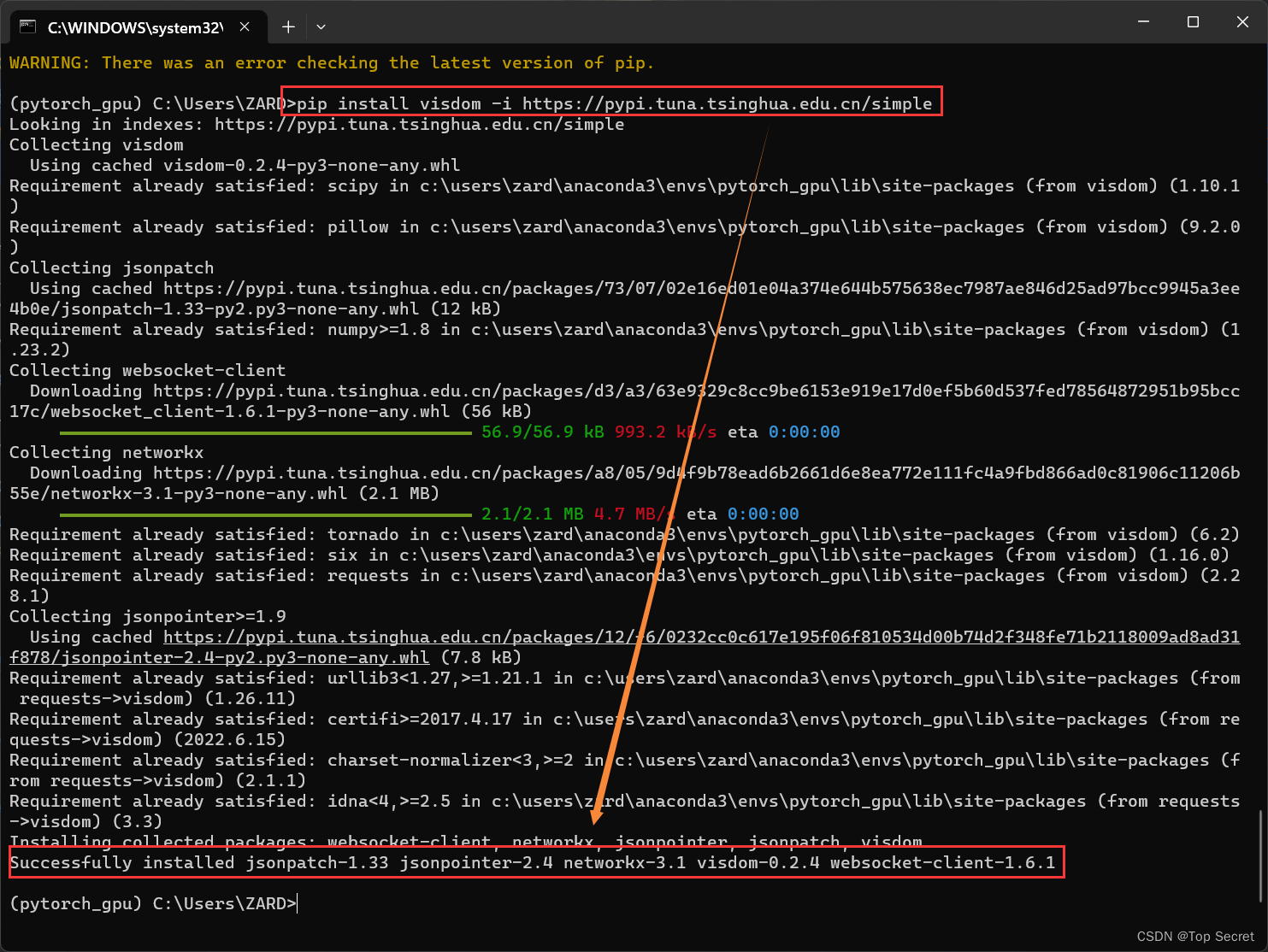
【算法代码】

#include<bits/stdc++.h>
using namespace std;

const int maxn=1e6+5;
int v[maxn],lid[maxn],rid[maxn];
int ans;

bool flag=0;
int getN(int x,int y) {
    if(x==-1 && y==-1) return 0;
    if(x==-1 || y==-1 || v[x]!=v[y]) {
        flag=1;
        return 0;
    }
    return getN(lid[x],rid[y])+getN(rid[x],lid[y])+2;
}

int main() {
    int n;
    cin>>n;
    for(int i=1; i<=n; i++) cin>>v[i];
    for(int i=1; i<=n; i++) cin>>lid[i]>>rid[i];
    for(int i=1; i<=n; i++) {
        flag=false;
        int sum=getN(lid[i],rid[i])+1;
        if(!flag) ans=max(ans,sum);
    }
    cout<<ans;
    return 0;
}


/*
in:
10
2 2 5 5 5 5 4 4 2 3
9 10
-1 -1
-1 -1
-1 -1
-1 -1
-1 2
3 4
5 6
-1 -1
7 8

out:
3
*/

【参考文献】
https://blog.csdn.net/qq_41431457/article/details/89339153
https://www.acwing.com/solution/content/133039/
https://www.acwing.com/solution/content/20417/