文章目录
- 数位DP
- 前置知识——位运算与集合论
- 例题——2376. 统计特殊整数
- 思路
- 代码模板(重要!⭐⭐⭐⭐⭐)
- 针对这道题,可以去掉 isNum 参数
- 相关题目练习
- 233. 数字 1 的个数⭐⭐⭐⭐⭐
- 代码模板修改——记录cnt(前面已经选了几个1)
- 代码优化——不需要isNum
- 面试题 17.06. 2出现的次数
- 600. 不含连续1的非负整数⭐⭐⭐
- 902. 最大为 N 的数字组合
- 1067. 范围内的数字计数
- 1397. 找到所有好字符串⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
- 数位dp + kmp
- 代码1——kmp风格1
- 代码2——kmp风格2(j从-1开始)👍👍👍👍👍
- kmp应用的相关题目——1392. 最长快乐前缀
- 解法1——kmp
- 解法2——Rabin-Karp 字符串编码
- 1012. 至少有 1 位重复的数字
- 解法——转换(统计特殊整数)
- 2719. 统计整数数目⭐⭐⭐
数位DP
https://www.bilibili.com/video/BV1rS4y1s721/
可以看完视频讲解之后直接写例题,学模板。
当前位填的数字会受到前面填的数字的约束。
前置知识——位运算与集合论

两个关键的式子:
x >> d & 1。
x | (1 << d)。
>> 和 & 的运算优先级是一样的,所以从左往右进行计算。
例题——2376. 统计特殊整数
https://leetcode.cn/problems/count-special-integers/

思路
https://leetcode.cn/problems/count-special-integers/solutions/1746956/shu-wei-dp-mo-ban-by-endlesscheng-xtgx/

代码模板(重要!⭐⭐⭐⭐⭐)
用 mask 记录已经选了哪些数字
用 isNum 记录是否前面都是前导零
class Solution {
char[] s;
int[][] memo;
public int countSpecialNumbers(int n) {
s = String.valueOf(n).toCharArray();
int m = s.length;
memo = new int[m][1 << 10];
for (int i = 0; i < m; ++i) {
Arrays.fill(memo[i], -1); // -1表示没有被计算过
}
// 从下标0开始填,初始mask=0,isLimit=true,isNum=false
return f(0, 0, true, false);
}
// 返回从i开始填数字,i前面填的数字的集合是mask,能构造出的特殊正数的数目
// isLimit表示前面填的数字是否都是n对应位上的,如果为true,那么当前位至多为s[i],否则至多为'9'
// isNum表示前面是否填了数字(是否跳过),如果为true,那么当前位可以从0开始,如果为false,那么我们可以跳过或者从1开始填数字 这个是为了处理无效的前导零(isNum=true表示前面都是前导零被跳过了)
int f(int i, int mask, boolean isLimit, boolean isNum) {
if (i == s.length) return isNum? 1: 0;
if (!isLimit && isNum && memo[i][mask] != -1) return memo[i][mask];
int res = 0;
// 可以跳过当前位
if (!isNum) res = f(i + 1, mask, false, false);
// 如果前面填的数字都和n一样,那么这一位至多填数字s[i](否则就超过n了)
int up = isLimit? s[i] - '0': 9;
for (int d = isNum? 0: 1; d <= up; ++d) {
if ((mask >> d & 1) == 0) {
res += f(i + 1, mask | (1 << d), isLimit && d == up, true);
}
}
if (!isLimit && isNum) memo[i][mask] = res;
return res;
}
}
一定要注意!
memo[i][mask] 记录的是当 !isLimit && isNum 时 对应 i 和 mask 的结果。(即不受约束且是数字)
因为真正 isLimit = true 到最后只有一次计算;(因为 true 就表示前面选择的数字的各位和 n 的各位是一样的。)
同理 isNum = false 时也是。(因为 false 就表示前面选择的数字都是前导零。)
这些情况在递归的过程中都只会遇到一次。

这里的状态个数为
l
e
n
(
s
)
∗
2
1
0
len(s) * 2^10
len(s)∗210,即
m
∗
2
D
m * 2^D
m∗2D ,这里的 D = 10,
2
D
2 ^ D
2D即为 mask 的数量。
针对这道题,可以去掉 isNum 参数
由于 mask 中记录了数字,可以通过判断 mask 是否为 0 来判断前面是否填了数字,所以 isNum 可以省略。
代码如下:
class Solution {
char[] s;
int[][] memo;
public int countSpecialNumbers(int n) {
s = String.valueOf(n).toCharArray();
int m = s.length;
memo = new int[m][1 << 10];
for (int i = 0; i < m; ++i) {
Arrays.fill(memo[i], -1); // -1表示没有被计算过
}
// 从下标0开始填,初始mask=0,isLimit=true
return f(0, 0, true);
}
// 返回从i开始填数字,i前面填的数字的集合是mask,能构造出的特殊正数的数目
// isLimit表示前面填的数字是否都是n对应位上的,如果为true,那么当前位至多为s[i],否则至多为'9'
int f(int i, int mask, boolean isLimit) {
if (i == s.length) return mask != 0? 1: 0;
if (!isLimit && mask != 0 && memo[i][mask] != -1) return memo[i][mask];
int res = 0;
// 可以跳过当前位
if (mask == 0) res = f(i + 1, mask, false);
// 如果前面填的数字都和n一样,那么这一位至多填数字s[i](否则就超过n了)
int up = isLimit? s[i] - '0': 9;
for (int d = mask != 0? 0: 1; d <= up; ++d) {
if ((mask >> d & 1) == 0) {
res += f(i + 1, mask | (1 << d), isLimit && d == up);
}
}
if (!isLimit && mask != 0) memo[i][mask] = res;
return res;
}
}
相关题目练习
233. 数字 1 的个数⭐⭐⭐⭐⭐
https://leetcode.cn/problems/number-of-digit-one/
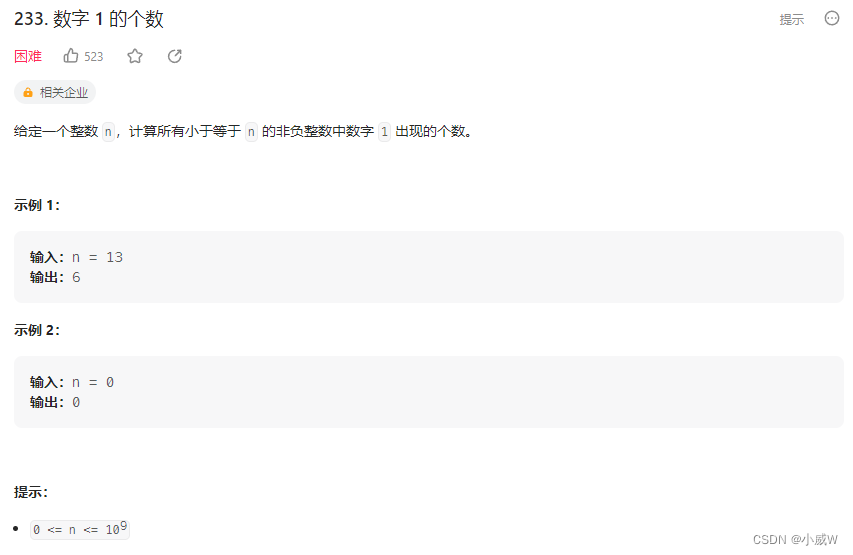
代码模板修改——记录cnt(前面已经选了几个1)
memo[i][j] 表示枚举到第 i 个下标时前面已经选择了 j 个1。
即 memo 数组的第二个维度是 cnt
class Solution {
char[] s;
int[][] memo;
public int countDigitOne(int n) {
s = Integer.toString(n).toCharArray();
int m = s.length;
memo = new int[m][m];
for (int i = 0; i < m; ++i) Arrays.fill(memo[i], -1);
return f(0, true, false, 0); // 最后一个参数表示前面选了几个1;
}
public int f(int i, boolean isLimit, boolean isNum, int cnt) {
if (i == s.length) return cnt;
if (!isLimit && isNum && memo[i][cnt] != -1) return memo[i][cnt];
int res = 0;
if (!isNum) res = f(i + 1, false, false, 0);
int up = isLimit? s[i] - '0': 9;
for (int d = isNum? 0: 1; d <= up; ++d) {
res += f(i + 1, isLimit && d == up, true, cnt + (d == 1? 1: 0));
}
if (!isLimit && isNum) memo[i][cnt] = res;
return res;
}
}
代码优化——不需要isNum
这道题目不需要 isNum,因为就算是前导零,也不会影响 数字中 1 的个数。
class Solution {
char[] s;
int[][] memo;
public int countDigitOne(int n) {
s = Integer.toString(n).toCharArray();
int m = s.length;
memo = new int[m][m];
for (int i = 0; i < m; ++i) Arrays.fill(memo[i], -1);
return f(0, true, 0); // 最后一个参数表示前面选了几个1;
}
public int f(int i, boolean isLimit, int cnt) {
if (i == s.length) return cnt;
if (!isLimit && memo[i][cnt] != -1) return memo[i][cnt];
int res = 0;
int up = isLimit? s[i] - '0': 9;
for (int d = 0; d <= up; ++d) {
res += f(i + 1, isLimit && d == up, cnt + (d == 1? 1: 0));
}
if (!isLimit) memo[i][cnt] = res;
return res;
}
}
面试题 17.06. 2出现的次数
https://leetcode.cn/problems/number-of-2s-in-range-lcci/
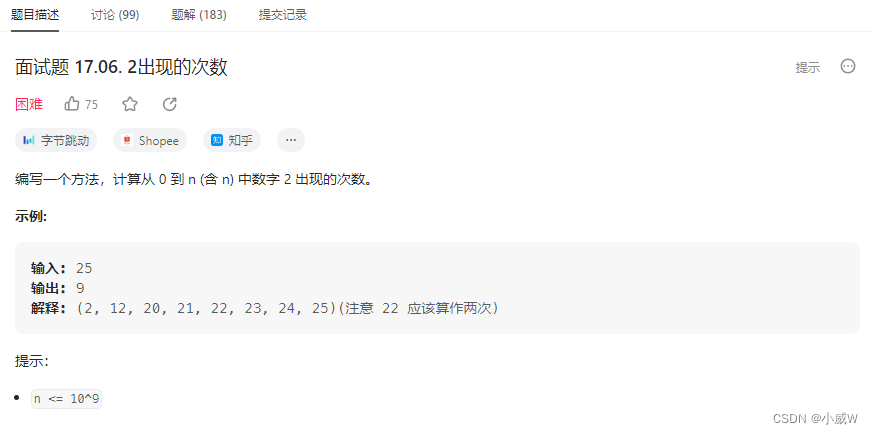
这道题目和上面那道题目几乎一模一样。
AC 代码如下:
class Solution {
int[][] memo;
char[] s;
public int numberOf2sInRange(int n) {
s = Integer.toString(n).toCharArray();
int m = s.length;
memo = new int[m][m];
return f(0, true, 0);
}
public int f(int i, boolean isLimit, int cnt) {
if (i == s.length) return cnt;
if (!isLimit && memo[i][cnt] !=0) return memo[i][cnt];
int res = 0, up = isLimit? s[i] - '0': 9;
for (int d = 0; d <= up; ++d) {
res += f(i + 1, isLimit && d == up, cnt + (d == 2? 1: 0));
}
if (!isLimit) memo[i][cnt] = res;
return res;
}
}
600. 不含连续1的非负整数⭐⭐⭐
600. 不含连续1的非负整数

将问题转换成只能选择 0 和 1 ,且 1 之间不能连续出现的数位 dp 问题即可。
class Solution {
char[] s;
int[][] memo;
public int findIntegers(int n) {
s = Integer.toBinaryString(n).toCharArray();
int m = s.length;
memo = new int[m][2];
for (int i = 0; i < m; ++i) Arrays.fill(memo[i], -1);
return f(0, true, 0);
}
public int f(int i, boolean isLimit, int last) {
if (i == s.length) return 1;
if (!isLimit && memo[i][last] != -1) return memo[i][last];
int up = isLimit? s[i] - '0': 1;
int res = f(i + 1, isLimit && up == 0, 0);
if (last != 1 && up == 1) res += f(i + 1, isLimit && up == 1, 1) ;
if (!isLimit) memo[i][last] = res;
return res;
}
}
902. 最大为 N 的数字组合
902. 最大为 N 的数字组合

class Solution {
Set<Integer> digits = new HashSet();
char[] s;
int[] memo;
public int atMostNGivenDigitSet(String[] digits, int n) {
for (String d: digits) this.digits.add(Integer.parseInt(d));
s = String.valueOf(n).toCharArray();
int m = s.length;
memo = new int[m];
Arrays.fill(memo, -1); // -1表示没有被计算过
// 从下标0开始填,isLimit=true,isNum=false
return f(0, true, false);
}
public int f(int i, boolean isLimit, boolean isNum) {
if (i == s.length) return isNum? 1: 0;
if (!isLimit && isNum && memo[i] != -1) return memo[i];
int res = 0;
// 可以跳过当前位
if (!isNum) res = f(i + 1, false, false);
// 如果前面填的数字都和n一样,那么这一位至多填数字s[i](否则就超过n了)
int up = isLimit? s[i] - '0': 9;
for (int d = isNum? 0: 1; d <= up; ++d) {
if (digits.contains(d)) {
res += f(i + 1, isLimit && d == up, true);
}
}
if (!isLimit && isNum) memo[i] = res;
return res;
}
}
删去了 mask ,因为它允许数字重复。
增加了一个可选数字集合 digits,每一位可选的数字必须在这个集合内。

1067. 范围内的数字计数
https://leetcode.cn/problems/digit-count-in-range/
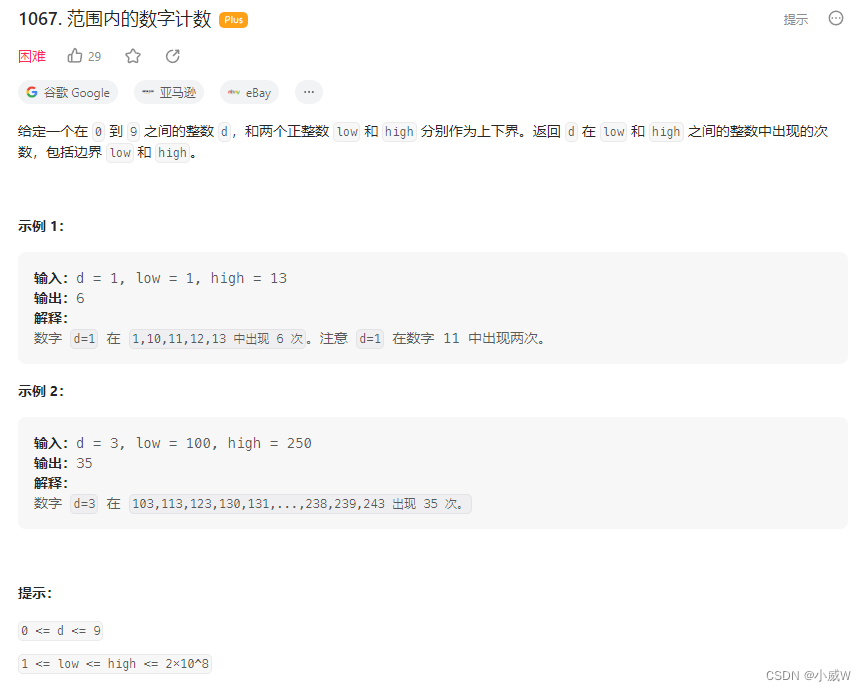
上面题目的变式题。
class Solution {
char[] s;
int[][] memo;
int t;
public int digitsCount(int d, int low, int high) {
t = d;
return op(high) - op(low - 1);
}
public int op(int n) {
s = Integer.toString(n).toCharArray();
int m = s.length;
memo = new int[m][m];
for (int i = 0; i < m; ++i) Arrays.fill(memo[i], -1);
return f(0, true, false, 0);
}
public int f(int i, boolean isLimit, boolean isNum, int cnt) {
if (i == s.length) return cnt;
if (!isLimit && isNum && memo[i][cnt] != -1) return memo[i][cnt];
int res = 0;
if (!isNum) res = f(i + 1, false, false, 0); // 前面是前导零,这里可以也跳过设置成零
int up = isLimit? s[i] - '0': 9;
for (int d = isNum? 0: 1; d <= up; ++d) {
res += f(i + 1, isLimit && d == up, true, cnt + (d == t? 1: 0));
}
if (!isLimit && isNum) memo[i][cnt] = res;
return res;
}
}
最开始写的时候忘记了 if (!isNum) res = f(i + 1, false, false, 0); 这一句。
1397. 找到所有好字符串⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐
1397. 找到所有好字符串

这题超级难!
数位dp + kmp
关于 kmp 可见:我一定要 学会KMP字符串匹配 。
代码1——kmp风格1
https://leetcode.cn/problems/find-all-good-strings/solutions/2195814/ling-shen-shu-wei-dpmo-ban-kmp-by-zachar-qcoo/
class Solution {
int n;
int[][] dp;
int[] next;
int MOD = (int)1e9 + 7;
public int findGoodStrings(int n, String s1, String s2, String evil) {
this.n = n;
int len = evil.length();
dp = new int[n][len];
for(int i = 0; i < n; i++) {
Arrays.fill(dp[i], -1);
}
next = new int[len];
for(int j = 0, i = 1; i < len; i++) {
while(j > 0 && evil.charAt(i) != evil.charAt(j)) j = next[j - 1];
if(evil.charAt(i) == evil.charAt(j)) j++;
next[i] = j;
}
return dfs(s1, s2, evil, 0, 0, true, true);
}
public int dfs(String s1, String s2, String evil, int i, int j, boolean downLimited, boolean upLimited) {
// 代表字符串中出现了 evil
if(j == evil.length()) return 0;
if(i == n) return 1;
if(!downLimited && !upLimited && dp[i][j] != -1) return dp[i][j];
long ans = 0;
char down = downLimited ? s1.charAt(i) : 'a', up = upLimited ? s2.charAt(i) : 'z';
for(char k = down; k <= up; k++) {
int nj = j;
while(nj > 0 && k != evil.charAt(nj)) nj = next[nj - 1];
// 此处要注意,当 nj == 0 的时候,会存在 k != evil.charAt(nj) 的情况
// 若直接 nj + 1 进入递归,是认为此时的两个字符一定是匹配上了,实际上可能并没有
if(nj == 0 && k != evil.charAt(nj)) nj = -1;
ans = (ans + dfs(s1, s2, evil, i + 1, nj + 1, downLimited && k == down, upLimited && k == up)) % MOD;
}
if(!downLimited && !upLimited) dp[i][j] = (int)ans;
return (int)ans;
}
}
代码2——kmp风格2(j从-1开始)👍👍👍👍👍
这是笔者自己根据上面代码修改来的。
dp[i][j] 表示枚举到第 i 位,前面匹配成功了evil 中的 j + 1 个字符(即 j 是 evil 的下标)。
class Solution {
int n;
int[][] dp;
int[] next; // kmp的next数组
int MOD = (int)1e9 + 7;
public int findGoodStrings(int n, String s1, String s2, String evil) {
this.n = n;
int len = evil.length();
dp = new int[n][len];
for(int i = 0; i < n; i++) {
Arrays.fill(dp[i], -1);
}
next = new int[len];
next[0] = -1;
for(int j = -1, i = 1; i < len; i++) {
while(j != -1 && evil.charAt(i) != evil.charAt(j + 1)) j = next[j];
if(evil.charAt(i) == evil.charAt(j + 1)) j++;
next[i] = j;
}
// 注意j初始为-1,表示一个都还没被匹配到
return dfs(s1, s2, evil, 0, -1, true, true);
}
public int dfs(String s1, String s2, String evil, int i, int j, boolean downLimited, boolean upLimited) {
// 代表字符串中出现了 evil
if(j == evil.length() - 1) return 0;
if(i == n) return 1;
if(!downLimited && !upLimited && dp[i][j + 1] != -1) return dp[i][j + 1]; // 注意所有的dp都是dp[i][j + 1],因为j是从-1开始的
long ans = 0;
char down = downLimited ? s1.charAt(i) : 'a', up = upLimited ? s2.charAt(i) : 'z';
for(char k = down; k <= up; k++) {
// kmp的匹配过程
int nj = j;
while(nj != -1 && k != evil.charAt(nj + 1)) nj = next[nj];
if (k == evil.charAt(nj + 1)) nj++;
ans = (ans + dfs(s1, s2, evil, i + 1, nj, downLimited && k == down, upLimited && k == up)) % MOD;
}
if(!downLimited && !upLimited) dp[i][j + 1] = (int)ans;
return (int)ans;
}
}
kmp应用的相关题目——1392. 最长快乐前缀
1392. 最长快乐前缀
解法1——kmp
kmp 的 next 数组即为最长公共前后缀数组。
class Solution {
public String longestPrefix(String s) {
int n = s.length();
int[] next = new int[n];
next[0] = -1;
for (int i = 1, j = -1; i < n; ++i) {
while (j != -1 && s.charAt(i) != s.charAt(j + 1)) j = next[j];
if (s.charAt(i) == s.charAt(j + 1)) j++;
next[i] = j;
}
return s.substring(0, next[n - 1] + 1);
}
}
解法2——Rabin-Karp 字符串编码
解析见:https://leetcode.cn/problems/longest-happy-prefix/solutions/172436/zui-chang-kuai-le-qian-zhui-by-leetcode-solution/
class Solution {
public String longestPrefix(String s) {
int n = s.length();
long prefix = 0, suffix = 0;
long base = 31, mod = 1000000007, mul = 1;
int happy = 0;
for (int i = 1; i < n; ++i) {
prefix = (prefix * base + (s.charAt(i - 1) - 'a')) % mod;
suffix = (suffix + (s.charAt(n - i) - 'a') * mul) % mod;
if (prefix == suffix) {
happy = i;
}
mul = mul * base % mod;
}
return s.substring(0, happy);
}
}
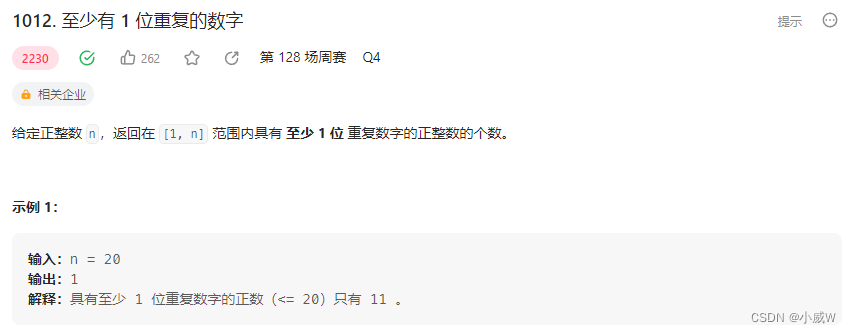
1012. 至少有 1 位重复的数字
1012. 至少有 1 位重复的数字
解法——转换(统计特殊整数)
用 n - 2376. 统计特殊整数 的结果就好了。
代码如下:
class Solution {
char[] s;
int[][] memo;
public int numDupDigitsAtMostN(int n) {
return n - countSpecialNumbers(n);
}
public int countSpecialNumbers(int n) {
s = String.valueOf(n).toCharArray();
int m = s.length;
memo = new int[m][1 << 10];
for (int i = 0; i < m; ++i) {
Arrays.fill(memo[i], -1); // -1表示没有被计算过
}
// 从下标0开始填,初始mask=0,isLimit=true
return f(0, 0, true);
}
// 返回从i开始填数字,i前面填的数字的集合是mask,能构造出的特殊正数的数目
// isLimit表示前面填的数字是否都是n对应位上的,如果为true,那么当前位至多为s[i],否则至多为'9'
int f(int i, int mask, boolean isLimit) {
if (i == s.length) return mask != 0? 1: 0;
if (!isLimit && mask != 0 && memo[i][mask] != -1) return memo[i][mask];
int res = 0;
// 可以跳过当前位
if (mask == 0) res = f(i + 1, mask, false);
// 如果前面填的数字都和n一样,那么这一位至多填数字s[i](否则就超过n了)
int up = isLimit? s[i] - '0': 9;
for (int d = mask != 0? 0: 1; d <= up; ++d) {
if ((mask >> d & 1) == 0) {
res += f(i + 1, mask | (1 << d), isLimit && d == up);
}
}
if (!isLimit && mask != 0) memo[i][mask] = res;
return res;
}
}
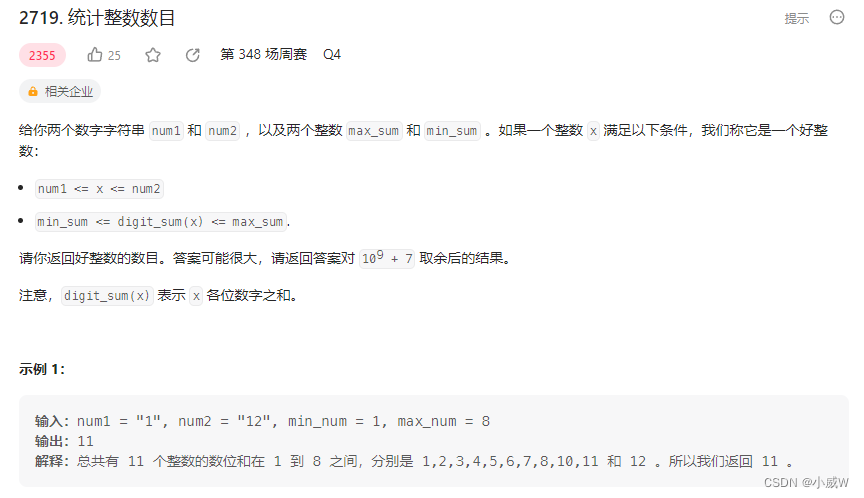
2719. 统计整数数目⭐⭐⭐
https://leetcode.cn/problems/count-of-integers/

class Solution {
char[] s;
int[][] memo;
int minSum, maxSum;
final int mod = (int)1e9 + 7;
public int count(String num1, String num2, int min_sum, int max_sum) {
minSum = min_sum;
maxSum = max_sum;
int ans = op(num2) - op(num1) + mod;
// 单独计算num1是否是合法的数字
int sum = 0;
for (char c: num1.toCharArray()) sum += c - '0';
if (min_sum <= sum && sum <= max_sum) ans++;
return ans % mod;
}
public int op(String num) {
s = num.toCharArray();
int m = s.length;
memo = new int[m][Math.min(9 * m, maxSum) + 1];
for (int i = 0; i < m; ++i) Arrays.fill(memo[i], -1);
return f(0, true, 0);
}
public int f(int i, boolean isLimit, int digitSum) {
if (digitSum > maxSum) return 0; // 非法数字
if (i == s.length) return digitSum >= minSum ? 1: 0;
if (!isLimit && memo[i][digitSum] != -1) return memo[i][digitSum];
int res = 0;
int up = isLimit? s[i] - '0': 9;
for (int d = 0; d <= up; ++d) {
res = (res + f(i + 1, isLimit && d == up, digitSum + d)) % mod;
}
if (!isLimit) memo[i][digitSum] = res;
return res;
}
}
这里由于 num1 是个字符串,所以直接计算 <= num1 的合法数字个数,再单独判断 num1 这个数是否合法。