题目描述:

1、思路
作为回溯算法的经典问题,常用的方法是,每次dfs前先判断是否达到临界条件,满足条件则加入结果集并return。通过循环和dfs来构建树,查找出全部满足条件的集合。
例如本题,如1,2,3的排列组合,可以先选1,然后选2or3,选了2然后只可以选3,依此类推。
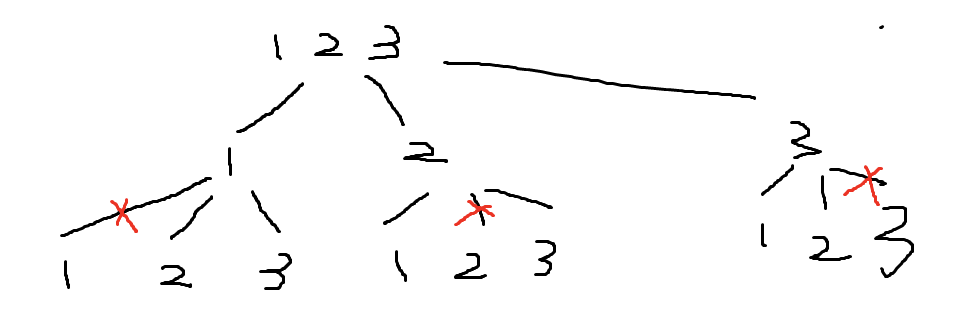
实际上,回溯的dfs就是在纵向地深度遍历,for循环就是在横向地遍历。
剪枝:
首先,每次选了1以后,下一次肯定不能选1;如果已经选了1,2,那么下一次就不能选1和2,因此我们需要构建一个used数组来记录每个数字是否被选择,在每次循环开始前判断used是否被使用,从而实现剪枝。
但这样只能应付上图的无重复情况,对于下图这种情况,我们发现不仅每次深度搜索需要去重,横向的循环也需要:例如,选第一个1、第二个1 、2 与 第二个1 、第一个1、2 都是[1,1,2],是重复的组合,这也需要排除。

因此,我一开始就想,在每次循环内的开始,再加一个判断,只要当前元素和上一个元素不同(前提是有序数组),不就ok了?即,当循环到第二个1的时候,判断上一个是不是1,如果是,则return即可!见下面代码:
代码如下:
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
Deque<Integer> path = new ArrayDeque<>();
Arrays.sort(nums);
int len = nums.length;
boolean[] used = new boolean[len];//used false
backTrace(nums,path,used,len);
return res;
}
public void backTrace(int[] nums, Deque<Integer> path, boolean[] used,int len){
if(path.size() == len){
res.add(new ArrayList<>(path));
return;
}
for(int i = 0; i < len; i++){
if(used[i]){//保证深度搜索不会放置自己(不重复位置)
continue;
}
//这一步,出现错误:
if(i > 0 && nums[i] == nums[i-1])continue;//保证水平不重复元素
used[i] = true;
path.add(nums[i]);
backTrace(nums,path,used,len);
used[i] = false;
path.removeLast();
}
}
}哈哈,测试发现输出结果是个[ ],空集合。明明纵向的去重了,横向也去重了,是哪里出错了呢?一步一步思考发现了问题如下。

2.修正错误:
//修正
if(i > 0 && nums[i] == nums[i-1])continue; 对于这里的水平去重,的确,每一轮循环到i的时候都可以判断是否和i-1元素相同,来实现不会选择值一样的元素,能够完成图中橙色的叉叉的剪枝。
但是它在每一轮循环里,同时会剪掉纵向遍历过程的相同数字! 例如下图的绿色叉叉:
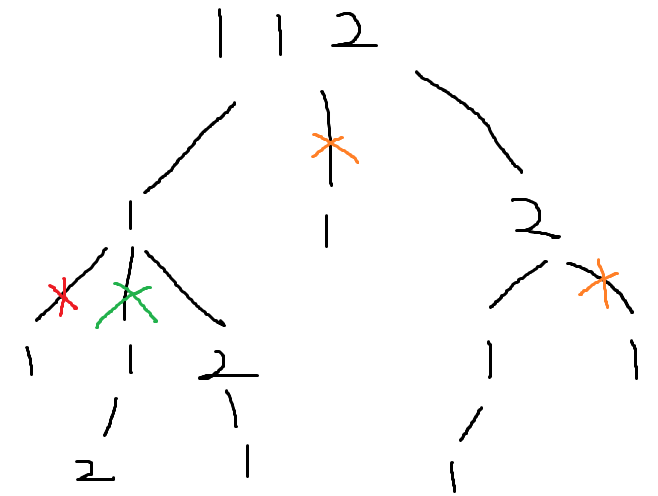
因为,在绿色叉叉这一层,[1,1,2]这样的组合,不能够说 第二个1 和 第 一个1相同就continue,那样的话这种正确答案就被排除了!
关键:也就是说,第一个1仍在被使用(true)的时候,是可以加入别的相同的1的。与之相反的,当第一个1被置为false后,这样的等值判断才有效。
因此可以这样修改代码,见注释:
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> permuteUnique(int[] nums) {
Deque<Integer> path = new ArrayDeque<>();
Arrays.sort(nums);
int len = nums.length;
boolean[] used = new boolean[len];//used false
backTrace(nums,path,used,len);
return res;
}
public void backTrace(int[] nums, Deque<Integer> path, boolean[] used,int len){
if(path.size() == len){
res.add(new ArrayList<>(path));
return;
}
for(int i = 0; i < len; i++){
if(used[i]){//保证深度搜索不会放置自己(不重复位置)
continue;
}
//只有在和上一个元素相等,并且上一个元素此时并没有被使用,
//说明已经执行了used[i] = false;说明已经用过,这才return。
//否则就是1,1,2的情况,第二个1是可以加入结果的。
if(i > 0 && nums[i] == nums[i-1] && !used[i-1])continue;//保证水平,不重复元素
used[i] = true;
path.add(nums[i]);
backTrace(nums,path,used,len);
used[i] = false;
path.removeLast();
}
}
} ok,答案正确。
这个题目涵盖了纵向和横向的两种剪枝,并且需要注意横向的剪枝判断对纵向剪枝的影响,需要仔细思考。