B-树（B-Tree）与二叉搜索树（BST）：讲讲数据库和文件系统背后的原理（读写比较大块数据的存储系统数据结构与算法原理）...

news2024/11/9 4:57:19

人类总喜欢发明创造一些新名词（比如说，简写/缩写/简称什么的），并通过这些名词把人群分成了三六九等。弄到最后，把自己都绕晕了。

你看，首先就是，B树，不要与Binary tree或B+tree混淆。

003ba7e05bc5c8d0f881b1d24534d4fa.png

B 树定义

B树是一种的平衡多路查找树，我们把树中结点最大的孩子数目称为B树的阶,通常记为m。

一棵m阶B树或为空树，或为满足如下特征的m叉树：

1）树中每个结点至多有m棵子树。（即至多含有m-1个关键字）（“两棵子树指针夹着一个关键字”）。

2）若根结点不是终端结点（最底层非叶子结点），则至少含有两棵子树。

3）除根结点外的所有非叶子结点至少含有 ceil(m/2) 棵子树。（即至少含有ceil(m/2)-1个关键字）。

200a004037eb2df73db4562b1063cb1d.png

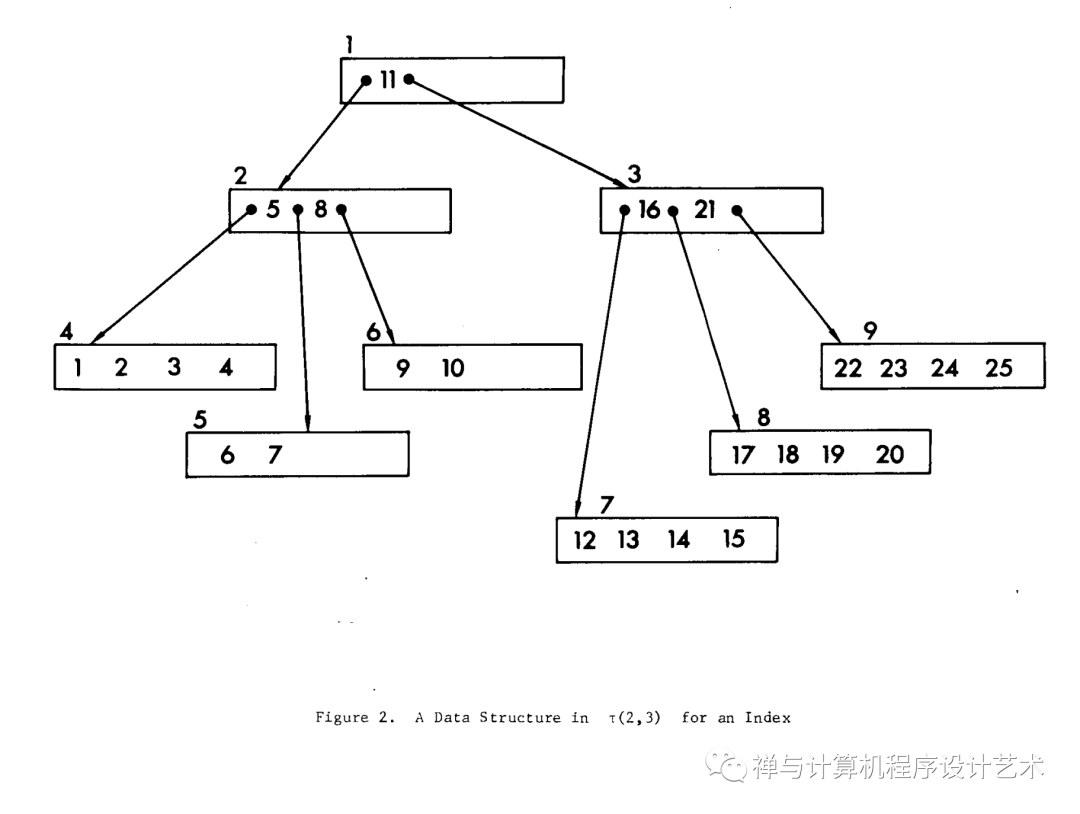16eb81758e6607f0526ca1d4a7f749a3.png在计算机科学中，B 树是一种自平衡树数据结构，它维护已排序的数据并允许在对数时间内进行搜索、顺序访问、插入和删除。B 树推广了二叉搜索树，允许节点有两个以上的孩子。[2]与其他自平衡二叉搜索树不同，B树非常适合读写比较大块数据的存储系统，比如数据库和文件系统。

In computer science, a B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children.[2] Unlike other self-balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as databases and file systems.

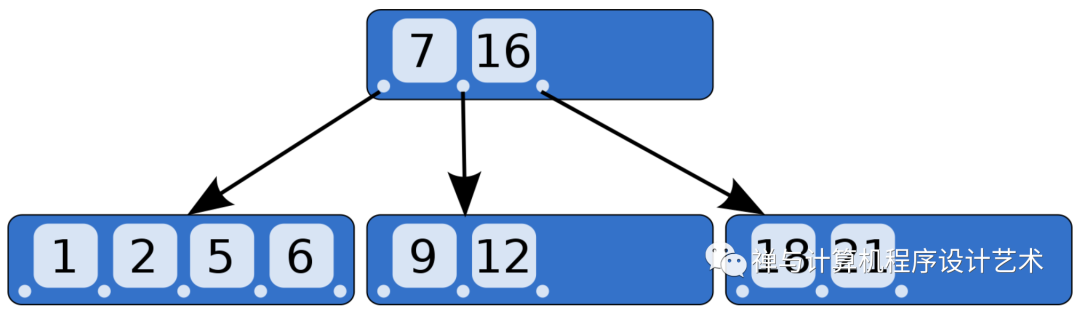
2b7a8de85a198e45101e9c92bbfbf373.png

B 树是一种特殊类型的自平衡搜索树，其中每个节点可以包含多个键，并且可以有两个以上的子节点。它是二叉搜索树的一般形式。

它也被称为高度平衡的 m 路树。

B-tree is a special type of self-balancing search tree in which each node can contain more than one key and can have more than two children. It is a generalized form of the binary search tree(BST).

It is also known as a height-balanced m-way tree.

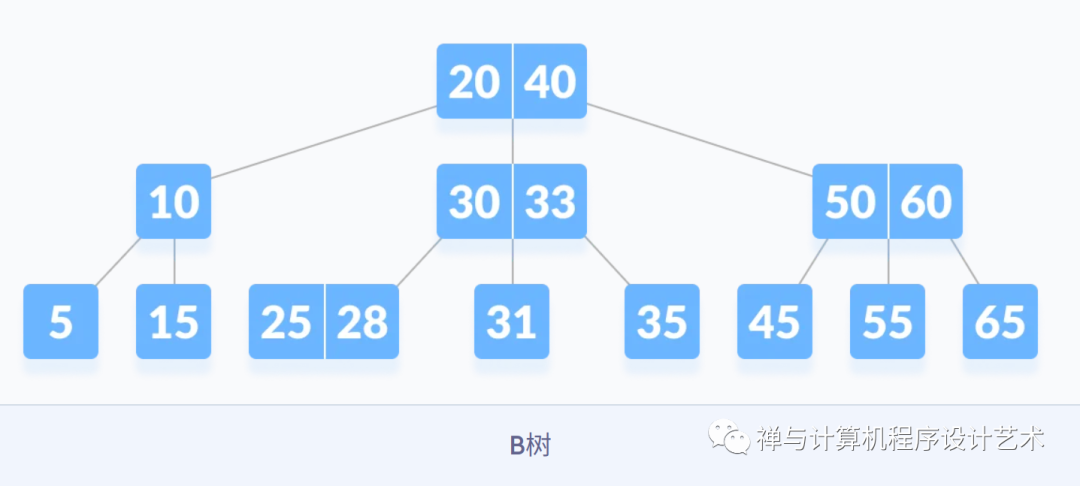
fdc087f758ce3feeaf9cb3ad26d6901c.png

B树查找过程

B树是多路查找树，二叉排序树是二路查找，B树是二叉排序树的拓展。

B树查找过程：

①先让待查找关键字key和结点中关键字比较，如果等于其中某个关键字，则查找成功。

②如果和所有关键字都不相等，则看key处在哪个范围内，然后去对应的指针所指向的子树查找。

起源

B 树是由Rudolf Bayer和Edward M. McCreight在波音研究实验室工作时发明的，目的是有效管理大型随机访问文件的索引页。基本假设是索引会非常庞大，以至于只有一小部分树可以放入主内存。Bayer 和 McCreight 的论文Organization and maintenance of large ordered indices [ 1]于 1970 年 7 月首次发行，后来发表在Acta Informatica上。[3]

Bayer 和 McCreight 从未解释过B代表什么（如果有的话） ：建议使用 Boeing、balanced、broad、bushy和Bayer。[4] [5] [6] McCreight 曾说过“你越想 B 树中 B 的含义，你就越了解 B 树。” [5]

定义

根据Knuth的定义，m阶 B 树（m order B Tree）是满足以下属性的树：[7]

  1. 每个节点至多有m个子节点。

  2. 每个内部节点至少有 ⌈ m /2⌉ 子节点。

  3. 每个非叶节点至少有两个孩子。

  4. 所有叶子都出现在同一水平面上。

  5. 具有k个子节点的非叶节点包含k -1 个键。

每个内部节点的键充当分隔其子树的分隔值。

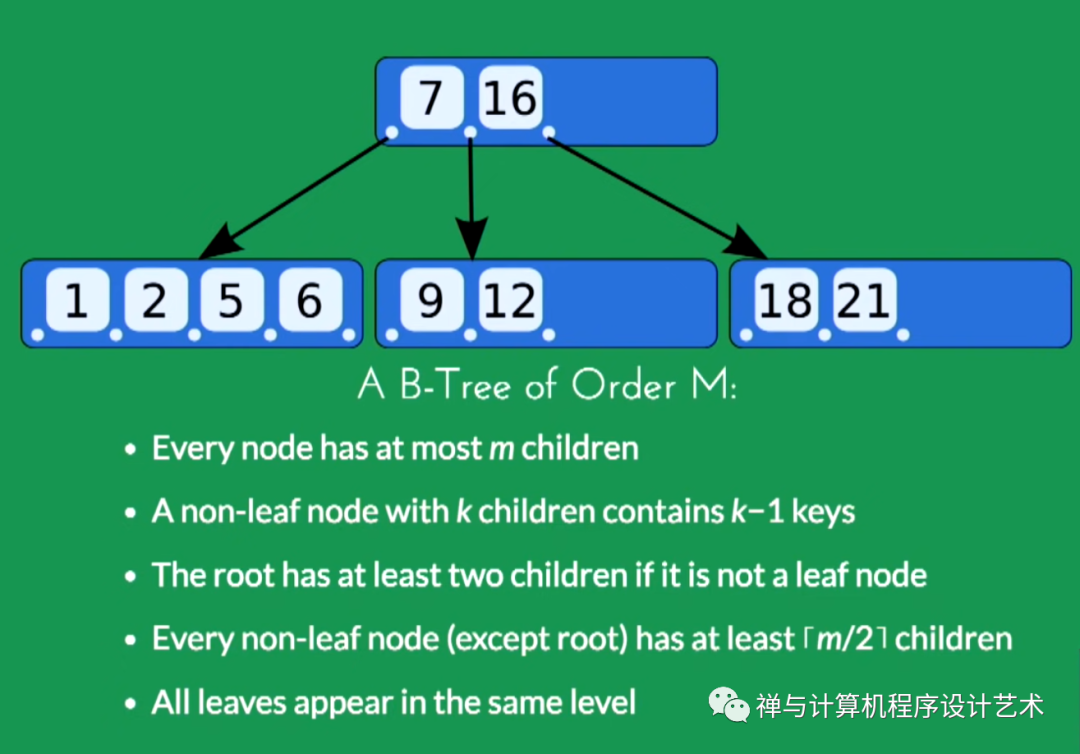
533adbb47b28e6d4eff9d63262d01f77.png

下图是一个 Order = 5 的 B Tree。

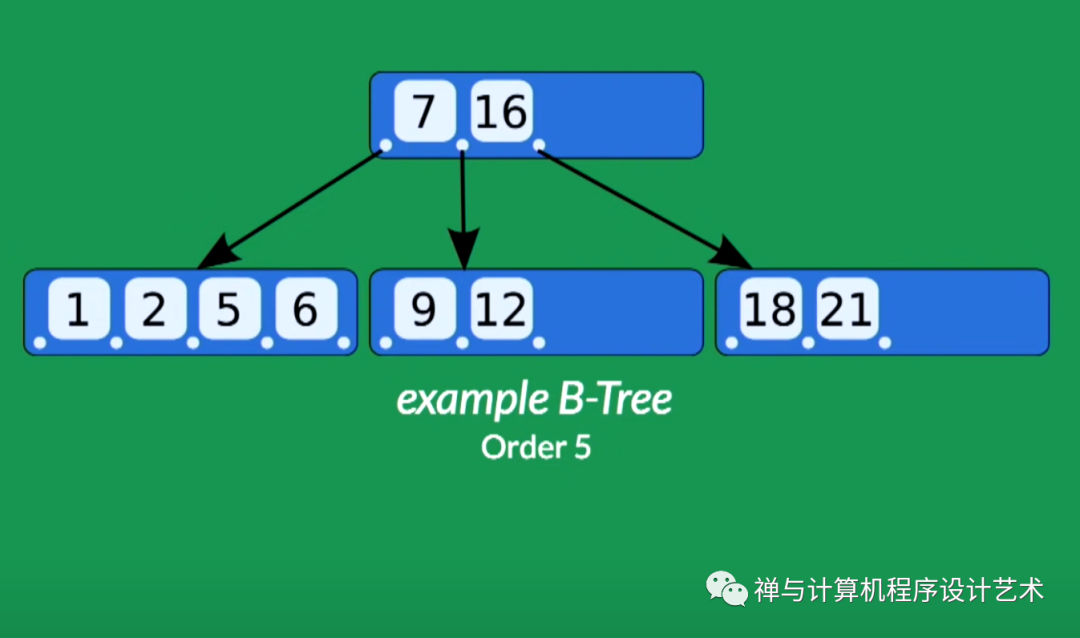
9a063eeb00e5852e01b6be2fd7a22908.png

Origin

B-trees were invented by Rudolf Bayer and Edward M. McCreight while working at Boeing Research Labs, for the purpose of efficiently managing index pages for large random-access files. The basic assumption was that indices would be so voluminous that only small chunks of the tree could fit in main memory. Bayer and McCreight's paper, Organization and maintenance of large ordered indices,[1] was first circulated in July 1970 and later published in Acta Informatica.[3]

Bayer and McCreight never explained what, if anything, the B stands for: Boeing, balanced, broad, bushy, and Bayer have been suggested.[4][5][6] McCreight has said that "the more you think about what the B in B-trees means, the better you understand B-trees."[5]

Definition

According to Knuth's definition, a B-tree of order m is a tree which satisfies the following properties:[7]

  1. Every node has at most m children.

  2. Every internal node has at least ⌈m/2⌉ children.

  3. Every non-leaf node has at least two children.

  4. All leaves appear on the same level.

  5. A non-leaf node with k children contains k−1 keys.

Each internal node's keys act as separation values which divide its subtrees.

为什么需要 B 树数据结构？

Why do you need a B-tree data strcuture?

随着访问硬盘等物理存储介质的时间越来越短，对 B 树的需求也随之增加。辅助存储设备速度较慢，容量较大。需要这种类型的数据结构来最大限度地减少磁盘访问。

其他数据结构如二叉搜索树、avl树、红黑树等只能在一个节点中存储一个键。如果你必须存储大量的键，那么这种树的高度就会变得非常大，访问时间也会增加。

但是，B-tree 可以在单个节点中存储许多键，并且可以有多个子节点。这显着降低了高度，允许更快的磁盘访问。

The need for B-tree arose with the rise in the need for lesser time in accessing the physical storage media like a hard disk. The secondary storage devices are slower with a larger capacity. There was a need for such types of data structures that minimize the disk accesses.

Other data structures such as a binary search tree, avl tree, red-black tree, etc can store only one key in one node. If you have to store a large number of keys, then the height of such trees becomes very large and the access time increases.

However, B-tree can store many keys in a single node and can have multiple child nodes. This decreases the height significantly allowing faster disk accesses.

B树应用

  • 数据库和文件系统

  • 存储数据块（辅助存储介质）

  • 多级索引

B Tree Applications

  • databases and file systems

  • to store blocks of data (secondary storage media)

  • multilevel indexing

B树操作源代码

// Searching a key on a B-tree in Java 


public class BTree {


  private int T;


  // Node creation
  public class Node {
    int n;
    int key[] = new int[2 * T - 1];
    Node child[] = new Node[2 * T];
    boolean leaf = true;


    public int Find(int k) {
      for (int i = 0; i < this.n; i++) {
        if (this.key[i] == k) {
          return i;
        }
      }
      return -1;
    };
  }


  public BTree(int t) {
    T = t;
    root = new Node();
    root.n = 0;
    root.leaf = true;
  }


  private Node root;


  // Search key
  private Node Search(Node x, int key) {
    int i = 0;
    if (x == null)
      return x;
    for (i = 0; i < x.n; i++) {
      if (key < x.key[i]) {
        break;
      }
      if (key == x.key[i]) {
        return x;
      }
    }
    if (x.leaf) {
      return null;
    } else {
      return Search(x.child[i], key);
    }
  }


  // Splitting the node
  private void Split(Node x, int pos, Node y) {
    Node z = new Node();
    z.leaf = y.leaf;
    z.n = T - 1;
    for (int j = 0; j < T - 1; j++) {
      z.key[j] = y.key[j + T];
    }
    if (!y.leaf) {
      for (int j = 0; j < T; j++) {
        z.child[j] = y.child[j + T];
      }
    }
    y.n = T - 1;
    for (int j = x.n; j >= pos + 1; j--) {
      x.child[j + 1] = x.child[j];
    }
    x.child[pos + 1] = z;


    for (int j = x.n - 1; j >= pos; j--) {
      x.key[j + 1] = x.key[j];
    }
    x.key[pos] = y.key[T - 1];
    x.n = x.n + 1;
  }


  // Inserting a value
  public void Insert(final int key) {
    Node r = root;
    if (r.n == 2 * T - 1) {
      Node s = new Node();
      root = s;
      s.leaf = false;
      s.n = 0;
      s.child[0] = r;
      Split(s, 0, r);
      insertValue(s, key);
    } else {
      insertValue(r, key);
    }
  }


  // Insert the node
  final private void insertValue(Node x, int k) {


    if (x.leaf) {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
        x.key[i + 1] = x.key[i];
      }
      x.key[i + 1] = k;
      x.n = x.n + 1;
    } else {
      int i = 0;
      for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
      }
      ;
      i++;
      Node tmp = x.child[i];
      if (tmp.n == 2 * T - 1) {
        Split(x, i, tmp);
        if (k > x.key[i]) {
          i++;
        }
      }
      insertValue(x.child[i], k);
    }


  }


  public void Show() {
    Show(root);
  }


  // Display
  private void Show(Node x) {
    assert (x == null);
    for (int i = 0; i < x.n; i++) {
      System.out.print(x.key[i] + " ");
    }
    if (!x.leaf) {
      for (int i = 0; i < x.n + 1; i++) {
        Show(x.child[i]);
      }
    }
  }


  // Check if present
  public boolean Contain(int k) {
    if (this.Search(root, k) != null) {
      return true;
    } else {
      return false;
    }
  }


  public static void main(String[] args) {
    BTree b = new BTree(3);
    b.Insert(8);
    b.Insert(9);
    b.Insert(10);
    b.Insert(11);
    b.Insert(15);
    b.Insert(20);
    b.Insert(17);


    b.Show();


    if (b.Contain(12)) {
      System.out.println("\nfound");
    } else {
      System.out.println("\nnot found");
    }
    ;
  }
}

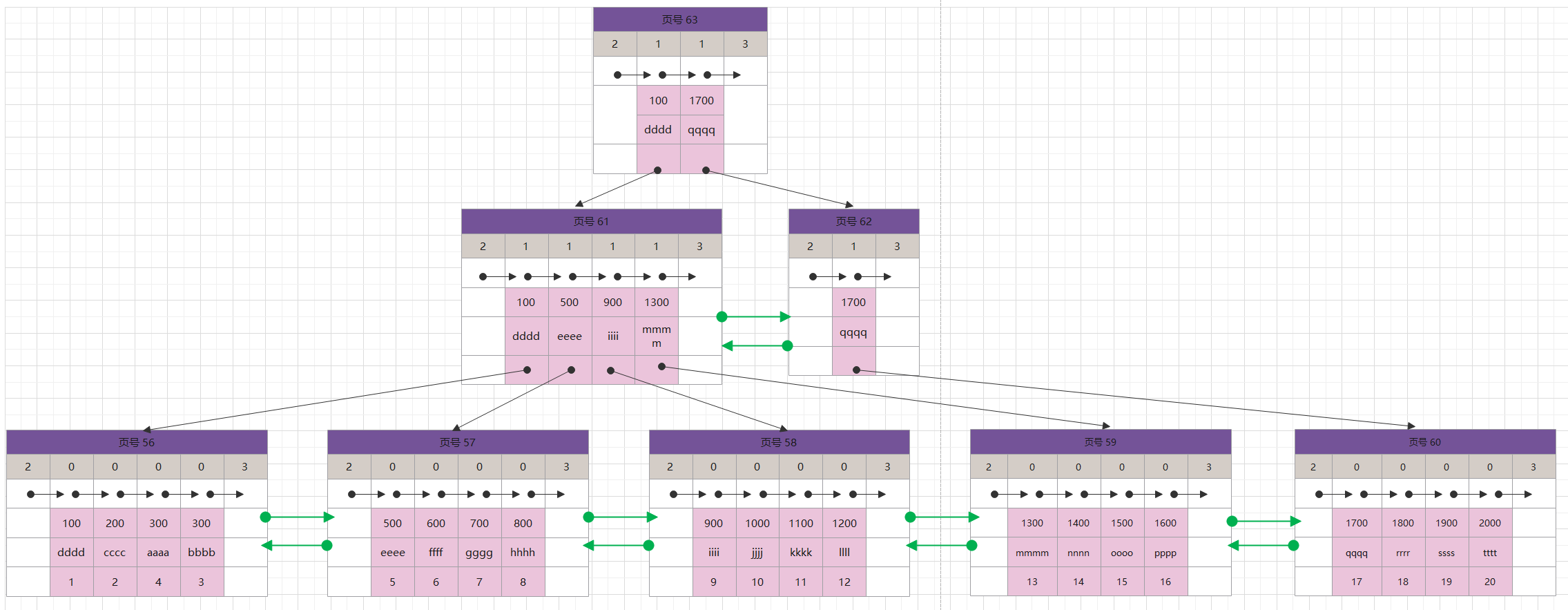
B+树

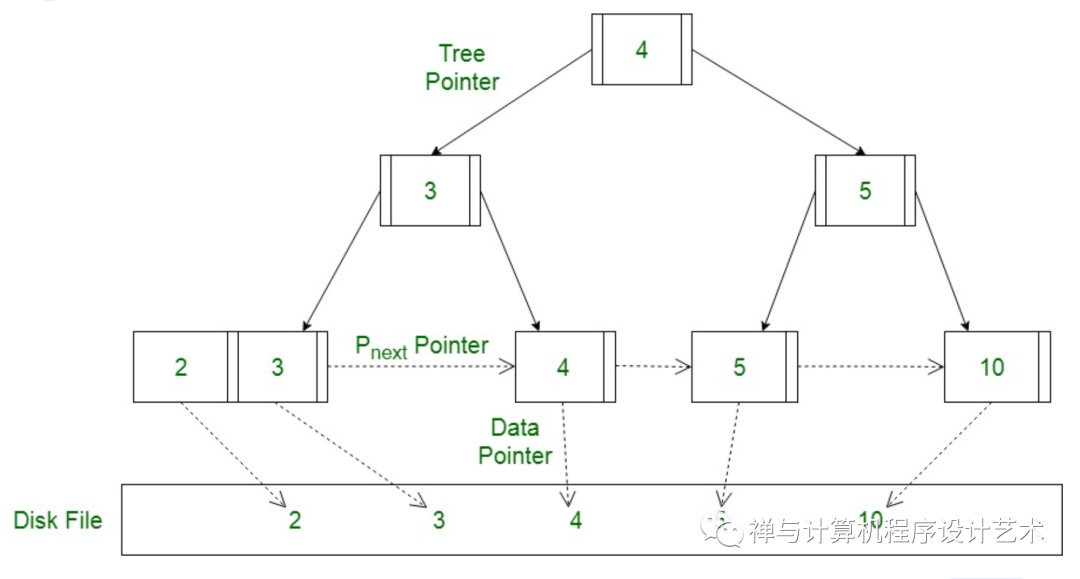
b6d59c9ccce13cea8a1ecfc8e1fa2c16.png

B+树是为磁盘和存储工具设计的一种数据结构，它是一种平衡查找树，它在查找，插入、修改方面的时间复杂度都稳定为 O(logn)。

节点

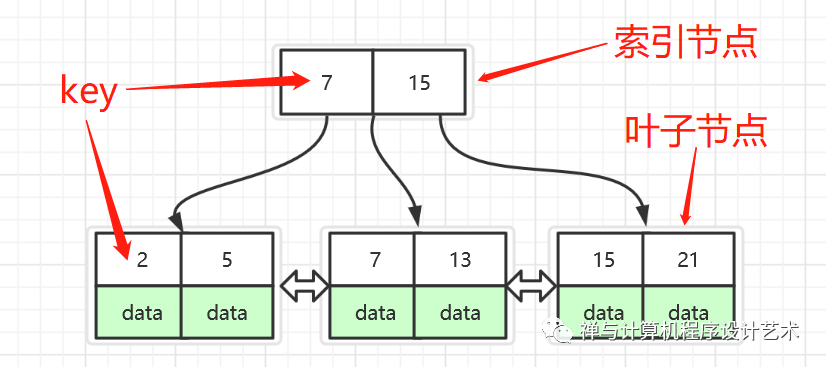
e3000effe64a5ffeb36ac8566b4acace.png

B+树节点是一组按照key有序的元素，B+树包含两种类型的节点，一种是索引节点，一种是叶子节点

  • 索引节点也叫内部节点，索引节点只包含key，不包含data, 节点的 key是升序排列的，对于指定的索引节点key来说，它左子树上所有的key都小于它的key，它右子树上所有的key都大于等于它的key

  • 叶节点上存储的是主键和数据(key和data), 所有的叶节点都在同一高度上，节点按key 从小到大并且通过指针使得彼此链接，这样，所有的叶节点组成了一个双向有序链表，叶节点这样做的好处是在不访问索引的情况下能顺序检索数据，也能很好的支持范围查询的快处理。

B+树特点

  • 阶数为 m 的B+树，每个索引节点最多有 m 个子节点，每个索引节点页面最多存储 m - 1 个索引key

  • 所有索引节点的子节点数在 Math.ceil(m / 2) 和 m 之间

  • B +树之所以称为平衡树，是因为从根节点到叶节点的每条路径都具有相同的长度。平衡树意味着所有对单个值的搜索都需要从磁盘读取相同数量的页面。

度数：在树中，每个节点的子节点（子树）的个数就称为该节点的度（degree）

阶数：（Order）阶定义为一个节点的子节点数目的最大值。（自带最大值属性）  

填充因子

B+树使用填充因子来控制页面的分裂和合并，设置数据占用页面空间的百分比，目的是为后面的数据预留一部分页空间，当有新数据时，可以放到预留的页空间中，避免分页的发生。默认的填充因子是50%，对于一棵m阶的B+树，填充因子是 m/2。

B+树是常用于数据库和操作系统的文件系统中的一种用于查找的数据结构。

m阶B+树与m阶的B树的主要差异在于：

（1）在B+树中，具有n个关键字的结点只含有n棵子树，即每个关键字对应一棵子树；而在B树中，具有n个结点的关键字含有（n+1）棵子树。

（2）在B+树中，每个结点（非根内部结点）关键字个数n的范围是ceil(m/2)<=n<=m(根节点1<=n<=m)，在B树中，每个结点（非根内部结点）关键字个数n的范围是ceil(m/2)-1<=n<=m-1（根节点：1<=n<=m-1）。

（3）在B+树中，叶结点包含信息，所有非叶结点仅起到索引作用，非叶结点中的每个索引项只含有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应记录的存储地址。

（4）在B+树中，叶结点包含了全部关键字，即在非叶结点中出现的关键字也会出现在叶节点中；而在B树中，叶结点包含的关键字和其他节点包含的关键字是不重复的。

（5）在B+树中，有一个指针指向关键字最小的叶子结点，所有叶子结点连接成一个链表。

Let’s see the difference between B-tree and B+ tree:

Basis of ComparisionB treeB+ tree
PointersAll internal and leaf nodes have data pointersOnly leaf nodes have data pointers
SearchSince all keys are not available at leaf, search often takes more time.All keys are at leaf nodes, hence search is faster and more accurate.
Redundant KeysNo duplicate of keys is maintained in the tree.Duplicate of keys are maintained and all nodes are present at the leaf.
InsertionInsertion takes more time and it is not predictable sometimes.Insertion is easier and the results are always the same.
DeletionDeletion of the internal node is very complex and the tree has to undergo a lot of transformations.Deletion of any node is easy because all node are found at leaf.
Leaf NodesLeaf nodes are not stored as structural linked list.Leaf nodes are stored as structural linked list.
AccessSequential access to nodes is not possibleSequential access is possible just like linked list
HeightFor a particular number nodes height is largerHeight is lesser than B tree for the same number of nodes
ApplicationB-Trees used in Databases, Search enginesB+ Trees used in Multilevel Indexing, Database indexing
Number of NodesNumber of nodes at any intermediary level ‘l’ is 2l.Each intermediary node can have n/2 to n children.

B+树的缺点： 

  • B 树的主要缺点是难以按顺序遍历键。B+树保留了B树的快速随机访问特性，同时也允许快速顺序访问。

B+树的应用：

  • 多级索引

  • 树上更快的操作（插入、删除、搜索）

  • 数据库索引

BST：binary search tree,二叉搜索树

5df3e57d0a3b14bd6b9869e65aa648c7.png

二叉搜索树是一种数据结构，可以让我们快速维护一个排序的数字列表。

之所以称为二叉树，是因为每个树节点最多有两个子节点。

它被称为搜索树，因为它可以用来及时搜索一个数字的存在O(log(n))。

将二叉搜索树与常规二叉树分开的属性是：

  1. 左子树的所有节点都小于根节点

  2. 右子树的所有节点都大于根节点

  3. 每个节点的两个子树也是 BST，即它们具有以上两个属性。

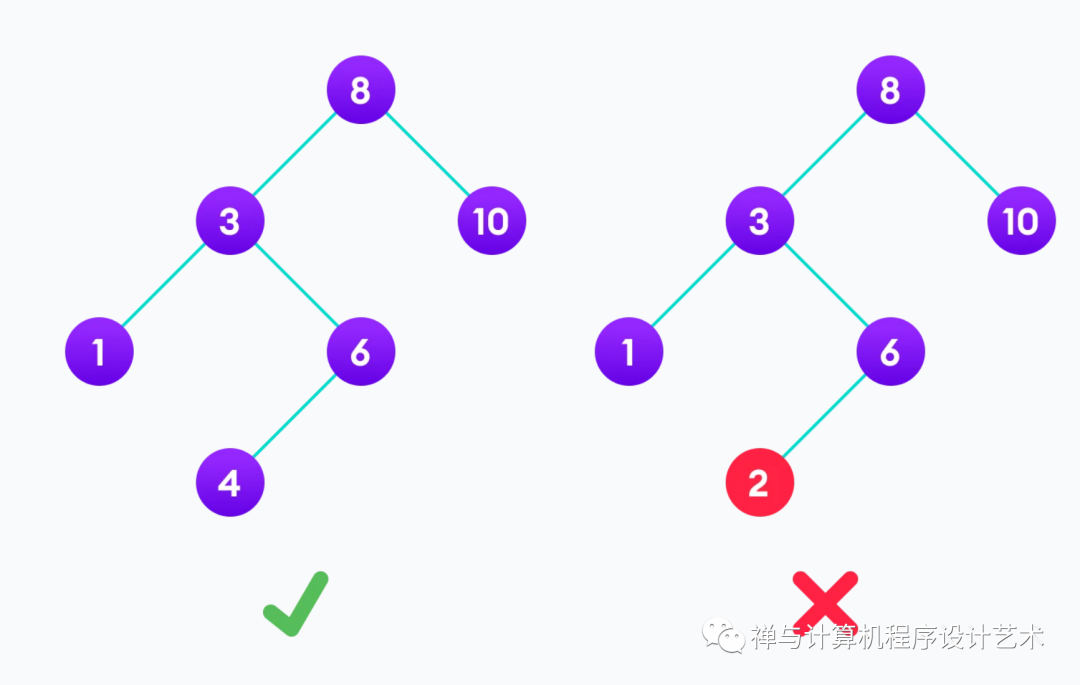
f5b6c0f97fc1ce382d0a4e29d2d6747b.png

上图中，右子树的一个值小于根的树表明它不是有效的二叉搜索树。

二叉搜索树应用

  1. 在数据库的多级索引中

  2. 用于动态排序

  3. 用于管理 Unix 内核中的虚拟内存区域

Binary Search Tree Applications

  1. In multilevel indexing in the database

  2. For dynamic sorting

  3. For managing virtual memory areas in Unix kernel

Binary Search Tree operations in C

// Binary Search Tree operations in C


#include <stdio.h>
#include <stdlib.h>


struct node {
  int key;
  struct node *left, *right;
};


// Create a node
struct node *newNode(int item) {
  struct node *temp = (struct node *)malloc(sizeof(struct node));
  temp->key = item;
  temp->left = temp->right = NULL;
  return temp;
}


// Inorder Traversal
void inorder(struct node *root) {
  if (root != NULL) {
    // Traverse left
    inorder(root->left);


    // Traverse root
    printf("%d -> ", root->key);


    // Traverse right
    inorder(root->right);
  }
}


// Insert a node
struct node *insert(struct node *node, int key) {
  // Return a new node if the tree is empty
  if (node == NULL) return newNode(key);


  // Traverse to the right place and insert the node
  if (key < node->key)
    node->left = insert(node->left, key);
  else
    node->right = insert(node->right, key);


  return node;
}


// Find the inorder successor
struct node *minValueNode(struct node *node) {
  struct node *current = node;


  // Find the leftmost leaf
  while (current && current->left != NULL)
    current = current->left;


  return current;
}


// Deleting a node
struct node *deleteNode(struct node *root, int key) {
  // Return if the tree is empty
  if (root == NULL) return root;


  // Find the node to be deleted
  if (key < root->key)
    root->left = deleteNode(root->left, key);
  else if (key > root->key)
    root->right = deleteNode(root->right, key);


  else {
    // If the node is with only one child or no child
    if (root->left == NULL) {
      struct node *temp = root->right;
      free(root);
      return temp;
    } else if (root->right == NULL) {
      struct node *temp = root->left;
      free(root);
      return temp;
    }


    // If the node has two children
    struct node *temp = minValueNode(root->right);


    // Place the inorder successor in position of the node to be deleted
    root->key = temp->key;


    // Delete the inorder successor
    root->right = deleteNode(root->right, temp->key);
  }
  return root;
}


// Driver code
int main() {
  struct node *root = NULL;
  root = insert(root, 8);
  root = insert(root, 3);
  root = insert(root, 1);
  root = insert(root, 6);
  root = insert(root, 7);
  root = insert(root, 10);
  root = insert(root, 14);
  root = insert(root, 4);


  printf("Inorder traversal: ");
  inorder(root);


  printf("\nAfter deleting 10\n");
  root = deleteNode(root, 10);
  printf("Inorder traversal: ");
  inorder(root);
}

红黑树

红黑树是二叉搜索树的一种。它像AVL 树一样是自平衡的，尽管它使用不同的属性来保持平衡的不变性。平衡二叉搜索树的搜索效率比不平衡二叉搜索树高得多，因此维持平衡所需的复杂性通常是值得的。它们被称为红黑树，因为树中的每个节点都被标记为红色或黑色。

In computer science, a red–black tree is a kind of self-balancing binary search tree. Each node stores an extra bit representing "color" ("red" or "black"), used to ensure that the tree remains balanced during insertions and deletions.

红黑树比 AVL 树保持稍微宽松的高度不变性。因为红黑树的高度稍大，在红黑树中查找会比较慢。然而，更宽松的高度不变性使得插入和删除更快。此外，由于相对容易实现，红黑树很受欢迎。

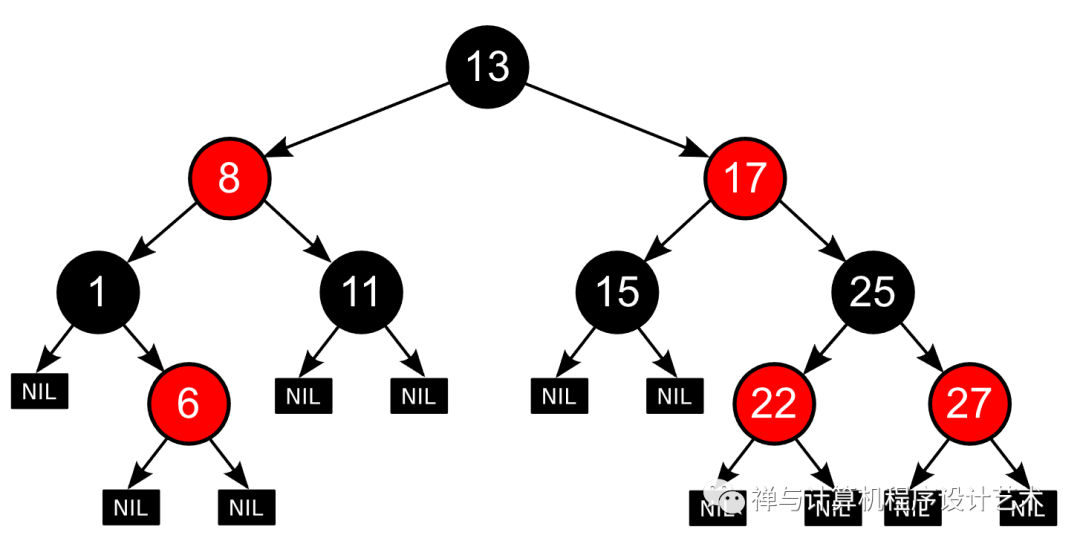
b7ec9776a52b408cbbc7953bbf7d7dcd.png

此图像显示了红黑树的表示。请注意每片叶子实际上是一个黑色的空值。这些属性对于证明树的高度不变性很重要。

概述

红黑树类似于二叉搜索树，它由节点组成，每个节点最多有两个孩子。但是，有一些特定于红黑树的新属性。

红黑树是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。 

红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

红黑树是每个结点都带有颜色属性的二叉查找树，颜色或红色或黑色。 [3]  在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

  • 性质1. 结点是红色或黑色。 

  • 性质2. 根结点是黑色。 

  • 性质3. 所有叶子都是黑色。（叶子是NIL结点） 

  • 性质4. 每个红色结点的两个子结点都是黑色。（从每个叶子到根的所有路径上不能有两个连续的红色结点）

  • 性质5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。

这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。

因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。 

性质4保证了路径上不能有两个连续的红色结点。最短的可能路径都是黑色结点，最长的可能路径有交替的红色和黑色结点。因为根据性质5所有最长的路径都有相同数目的黑色结点，这就表明了没有路径能多于任何其他路径的两倍长。 

因为红黑树是一种特化的二叉查找树，所以红黑树上的只读操作与普通二叉查找树相同。

红黑树的数据结构模型

// Basic type definitions:

enum color_t { BLACK, RED };

struct RBnode {     // node of red–black tree
  RBnode* parent;   // == NULL if root of the tree
  RBnode* child[2]; // == NIL if child is empty
    // Index is:
    //   LEFT  := 0, if (key < parent->key)
    //   RIGHT := 1, if (key > parent->key)
  enum color_t color;
  int key;
};

#define NIL   NULL // null pointer  or  pointer to sentinel node
#define LEFT  0
#define RIGHT 1
#define left  child[LEFT]
#define right child[RIGHT]

struct RBtree { // red–black tree
  RBnode* root; // == NIL if tree is empty
};

// Get the child direction (∈ { LEFT, RIGHT })
//   of the non-root non-NIL  RBnode* N:
#define childDir(N) ( N == (N->parent)->right ? RIGHT : LEFT )

References

Bayer, R.; McCreight, E. (July 1970). "Organization and maintenance of large ordered indices" (PDF). Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control - SIGFIDET '70. Boeing Scientific Research Laboratories. p. 107. doi:10.1145/1734663.1734671. S2CID 26930249.

 Comer 1979.

 Bayer & McCreight 1972.

 Comer 1979, p. 123 footnote 1.

 Weiner, Peter G. (30 August 2013). "4- Edward M McCreight" – via Vimeo.

 "Stanford Center for Professional Development". scpd.stanford.edu. Archived from the original on 2014-06-04. Retrieved 2011-01-16.

 Knuth 1998, p. 483.

 Folk & Zoellick 1992, p. 362.

 Folk & Zoellick 1992.

 Folk & Zoellick 1992, p. 363.

 Bayer & McCreight (1972) avoided the issue by saying an index element is a (physically adjacent) pair of (x, a) where x is the key, and a is some associated information. The associated information might be a pointer to a record or records in a random access, but what it was didn't really matter. Bayer & McCreight (1972) states, "For this paper the associated information is of no further interest."

 Folk & Zoellick 1992, p. 379.

 Knuth 1998, p. 488.

 Tomašević, Milo (2008). Algorithms and Data Structures. Belgrade, Serbia: Akademska misao. pp. 274–275. ISBN 978-86-7466-328-8.

 Rigin A. M., Shershakov S. A. (2019-09-10). "SQLite RDBMS Extension for Data Indexing Using B-tree Modifications". Proceedings of the Institute for System Programming of the RAS. Institute for System Programming of the RAS (ISP RAS). 31 (3): 203–216. doi:10.15514/ispras-2019-31(3)-16. S2CID 203144646. Retrieved 2021-08-29.

 Counted B-Trees, retrieved 2010-01-25

 Seagate Technology LLC, Product Manual: Barracuda ES.2 Serial ATA, Rev. F., publication 100468393, 2008 [1], page 6

 Kleppmann, Martin (2017), Designing Data-Intensive Applications, Sebastopol, California: O'Reilly Media, p. 80, ISBN 978-1-449-37332-0

 Jan Jannink. "Implementing Deletion in B+-Trees". Section "4 Lazy Deletion".

 Comer 1979, p. 127; Cormen et al. 2001, pp. 439–440

 "Deletion in a B-tree" (PDF). cs.rhodes.edu. Archived (PDF) from the original on 2022-10-09. Retrieved 24 May 2022.

 "Cache Oblivious B-trees". State University of New York (SUNY) at Stony Brook. Retrieved 2011-01-17.

 Mark Russinovich. "Inside Win2K NTFS, Part 1". Microsoft Developer Network. Archived from the original on 13 April 2008. Retrieved 2008-04-18.

 Matthew Dillon (2008-06-21). "The HAMMER Filesystem" (PDF). Archived (PDF) from the original on 2022-10-09.

 Lehman, Philip L.; Yao, s. Bing (1981). "Efficient locking for concurrent operations on B-trees". ACM Transactions on Database Systems. 6 (4): 650–670. doi:10.1145/319628.319663. S2CID 10756181.

 Wang, Paul (1 February 1991). "An In-Depth Analysis of Concurrent B-tree Algorithms" (PDF). dtic.mil. Archived from the original (PDF) on 4 June 2011. Retrieved 21 October 2022.

 "Downloads - high-concurrency-btree - High Concurrency B-Tree code in C - GitHub Project Hosting". GitHub. Retrieved 2014-01-27.

 "Lockless concurrent B-tree index meta access method for cached nodes".

General

Bayer, R.; McCreight, E. (1972), "Organization and Maintenance of Large Ordered Indexes" (PDF), Acta Informatica, 1 (3): 173–189, doi:10.1007/bf00288683, S2CID 29859053

Comer, Douglas (June 1979), "The Ubiquitous B-Tree", Computing Surveys, 11 (2): 123–137, doi:10.1145/356770.356776, ISSN 0360-0300, S2CID 101673.

Cormen, Thomas; Leiserson, Charles; Rivest, Ronald; Stein, Clifford (2001), Introduction to Algorithms (Second ed.), MIT Press and McGraw-Hill, pp. 434–454, ISBN 0-262-03293-7. Chapter 18: B-Trees.

Folk, Michael J.; Zoellick, Bill (1992), File Structures (2nd ed.), Addison-Wesley, ISBN 0-201-55713-4

Knuth, Donald (1998), Sorting and Searching, The Art of Computer Programming, vol. 3 (Second ed.), Addison-Wesley, ISBN 0-201-89685-0. Section 6.2.4: Multiway Trees, pp. 481–491. Also, pp. 476–477 of section 6.2.3 (Balanced Trees) discusses 2–3 trees.

Original papers

Bayer, Rudolf; McCreight, E. (July 1970), Organization and Maintenance of Large Ordered Indices, vol. Mathematical and Information Sciences Report No. 20, Boeing Scientific Research Laboratories.

Bayer, Rudolf (1971), Binary B-Trees for Virtual Memory, Proceedings of 1971 ACM-SIGFIDET Workshop on Data Description, Access and Control, San Diego, California.

https://www.programiz.com/dsa/binary-search-tree

https://brilliant.org/wiki/red-black-tree/

https://en.wikipedia.org/wiki/Red%E2%80%93black_tree

【更多阅读】

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/73964.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

有奖征文 | 当我们谈操作系统时，我们在谈什么？

有奖征文 | 当我们谈操作系统时，我们在谈什么？

OS&#xff0c;Operating System&#xff0c;操作系统&#xff0c;计算机中最基本也是最重要的基础性系统软件。1991 年&#xff0c;大二学生 Linus Torvalds 写出 Linux0.01&#xff0c;经过几十年的发展&#xff0c;以 Linux 为代表的服务器操作系统&#xff0c;成长为一个既…
阅读更多...
lambda之Stream流式编程

lambda之Stream流式编程

lambda之Stream流式编程 一、什么是 Stream Stream中文称为 “流”&#xff0c;通过将集合转换为这么一种叫做“流”的元素序列&#xff0c;通过声明性方式&#xff0c;能够对集合中的每个元素进行一系列并行或串行的流水线操作。换句话说&#xff0c;你只需要告诉流你的要求…
阅读更多...
led护眼台灯对眼睛好？过来人说说led护眼灯是否真的能护眼

led护眼台灯对眼睛好？过来人说说led护眼灯是否真的能护眼

众所周知&#xff0c;现在绝大部分光源都是使用led发光&#xff0c;无论是室内照明灯、室外装饰灯、气氛调节灯、工作学习护眼台灯等等&#xff0c;都是使用led灯珠&#xff0c;那么也就有人会问了&#xff1a;led灯真的对眼睛好吗&#xff1f;Led护眼台灯真的能护眼吗&#xf…
阅读更多...
TH7-搜附近

TH7-搜附近

TH7-搜附近说明1、探花1.1、查询推荐列表dubbo服务1.1.1、实体对象1.1.2、定义接口1.1.3、编写实现1.1.4、单元测试1.2、查询推荐列表APP接口实现1.2.1、TanHuaController1.2.2、TanHuaService1.2.3、测试1.3、喜欢的dubbo服务1.3.1、定义接口1.3.2、编写实现1.4、左滑右滑1.4.…
阅读更多...
fofa搜索漏洞技巧

fofa搜索漏洞技巧

fofa搜索漏洞技巧整理，主要有以下十个方面：搜索HTTP响应头中含有"thinkphp"关键词的网站和IP；加上标题带有后台的；加上时间，现在新网站有thinkphp日志泄露的有很多； 搜索html正文中含有"管理后台"关键词的网站和IP body="管理后台"等。 …
阅读更多...
Linux内核缓存

Linux内核缓存

【推荐阅读】 轻松学会linux下查看内存频率,内核函数,cpu频率 纯干货&#xff0c;linux内存管理——内存管理架构&#xff08;建议收藏&#xff09; 一篇长文叙述Linux内核虚拟地址空间的基本概括 页缓存和块缓存 内核为块设备提供了两种通用的缓存方案&#xff1a; 页缓存&a…
阅读更多...
光华股份深交所上市：市值51亿 应收账款余额超5亿

光华股份深交所上市：市值51亿 应收账款余额超5亿

雷递网 雷建平 12月8日浙江光华科技股份有限公司&#xff08;简称&#xff1a;“光华股份”&#xff0c;证券代码&#xff1a;001333&#xff09;今日在深交所主板上市。光华股份本次发行3200万股&#xff0c;发行价为27.76元&#xff0c;募资8.88亿元。光华股份开盘价为33.31元…
阅读更多...
开源，是不道德的！

开源，是不道德的！

原创&#xff1a;小姐姐味道&#xff08;微信公众号ID&#xff1a;xjjdog&#xff09;&#xff0c;欢迎分享&#xff0c;非公众号转载保留此声明。请删掉你的github开源代码&#xff0c;让CV工程师成为真正的工程师。不要做真正的代码分享&#xff0c;因为除了满足一下你的虚荣…
阅读更多...
vue-cli中学习vue

vue-cli中学习vue

vue部分知识 大部分学习内容及代码在gitee仓库 生命周期 基本介绍 生命周期描述beforeCreate组件实例被创建之初created组件实例已经完全创建beforeMount组件挂载之前mounted组件挂载到实例上去之后beforeUpdate组件数据发生变化&#xff0c;更新之前updated组件数据更新之后…
阅读更多...
springboot知识点

springboot知识点

基本介绍 微服务最早由Martin Fowler与James Lewis于2014年共同提出&#xff0c;微服务架构风格是一种使用一套小服务来开发单个应用的方式途径&#xff0c;每个服务运行在自己的进程中&#xff0c;并使用轻量级机制通信&#xff0c;通常是HTTP API&#xff0c;这些服务基于业…
阅读更多...
TH8-小视频方案

TH8-小视频方案

TH8-小视频方案说明1、我的访客1.1、dubbo服务1.1.1、实体对象1.1.2、定义接口1.1.3、编写实现1.2、记录访客数据1.3、首页谁看过我1.3.1、VO对象1.3.2、MovementController1.3.3、MovementService2、小视频功能说明3、FastDFS2.1、FastDFS是什么&#xff1f;2.2、工作原理2.1.…
阅读更多...
会员消费占比高达96%，孩子王究竟是怎么做到的？

会员消费占比高达96%，孩子王究竟是怎么做到的？

&#x1f446;点击关注公众号&#x1f446;1.孩子王&#xff1a;依靠会员“稳江山”2021年上半年&#xff0c;增长黑盒独家发布了一篇关于孩子王的研究文章《万字拆解孩子王&#xff1a;充满矛盾的母婴零售之王》&#xff0c;彼时&#xff0c;孩子王尚在二度上市的前夕等待敲钟…
阅读更多...
JAVA SCRIPT设计模式--行为型--设计模式之Template Method模板方法（22）

JAVA SCRIPT设计模式--行为型--设计模式之Template Method模板方法（22）

JAVA SCRIPT设计模式是本人根据GOF的设计模式写的博客记录。使用JAVA SCRIPT语言来实现主体功能&#xff0c;所以不可能像C&#xff0c;JAVA等面向对象语言一样严谨&#xff0c;大部分程序都附上了JAVA SCRIPT代码&#xff0c;代码只是实现了设计模式的主体功能&#xff0c;不代…
阅读更多...
2023最新SSM计算机毕业设计选题大全（附源码+LW）之java课程教学过程f6oz5

2023最新SSM计算机毕业设计选题大全（附源码+LW）之java课程教学过程f6oz5

对于即将毕业或者即将做课设的同学而言&#xff0c;由于经验的欠缺&#xff0c;面临的第一个难题就是选题&#xff0c;确定好题目之后便是开题报告&#xff0c;如果选题首先看自己学习那些技术&#xff0c;不同技术适合做不同的产品&#xff0c;比如自己会些简单的Java语言&…
阅读更多...
BSV 上的 Graftroot

BSV 上的 Graftroot

我们已经演示了如何使用无合约的合约在 BSV 上实现 Taproot。我们将展示了其后续提案 Graftroot 可以以类似的方式实施。 BTC 中的 Grabroot 与 Taproot 类似&#xff0c;有两种方式可以使用锁定在由多方创建的聚合公钥 P 中的资金&#xff1a; 合作案例&#xff1a;又名默认…
阅读更多...
kubernetes 安装 Harbor 仓库

kubernetes 安装 Harbor 仓库

文章目录kubernetes 安装 Harbor 仓库1. 下载 Harbor2. 安装 docker3. 优化 docker 配置4. 下载 docker-compose5. 安装 Harbor:one: 上传 harbor 文件包:two: 解压:three: 修改配置文件:four: 执行安装脚本安装:five: 配置开机自启6. 登陆测试:one: 浏览器登陆:two: 命令行登陆…
阅读更多...
为什么需要对相机标定？

为什么需要对相机标定？

以下内容来自系统教程如何搞定单目/鱼眼/双目/阵列 相机标定&#xff1f; 点击领取相机标定资料和代码 为什么需要对相机标定&#xff1f; 我们所处的世界是三维的&#xff0c;而相机拍摄的照片却是二维的&#xff0c;丢失了其中距离/深度的信息。从数学上可以简单理解为&…
阅读更多...
Peppol网络对接流程

Peppol网络对接流程

Peppol 代表泛欧在线公共采购&#xff0c;现在连接到 Peppol 的组织可以通过高度安全的国际网络交换商业文件。知行软件通过了 PEPPOL 的 AS2 及 AS4 测试&#xff0c;被 OpenPEPPOL AISBL 正式认证为 PEPPOL 接入点供应商。可以在Peppol查询到相关接入点信息&#xff0c;如下&…
阅读更多...
TH9-搭建后台系统

TH9-搭建后台系统

TH9-搭建后台系统1、项目架构1.1 概述1.2 API网关1.2.1 搭建网关依赖引导类跨域问题配置类配置文件1.2.2 配置鉴权管理器1.3 Nacos配置中心1.3.1 添加依赖1.3.2 添加bootstrap.yml配置1.3.3 nacos添加配置2、后台系统2.1 概述2.2 环境前端搭建2.2.1 导入数据库2.2.2 导入静态页…
阅读更多...
MYSQL-INNODB索引构成详解

MYSQL-INNODB索引构成详解

作者&#xff1a;郑啟龙 摘要&#xff1a; 对于MYSQL的INNODB存储引擎的索引&#xff0c;大家是不陌生的&#xff0c;都能想到是 B树结构&#xff0c;可以加速SQL查询。但对于B树索引&#xff0c;它到底“长”得什么样子&#xff0c;它具体如何由一个个字节构成的&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023