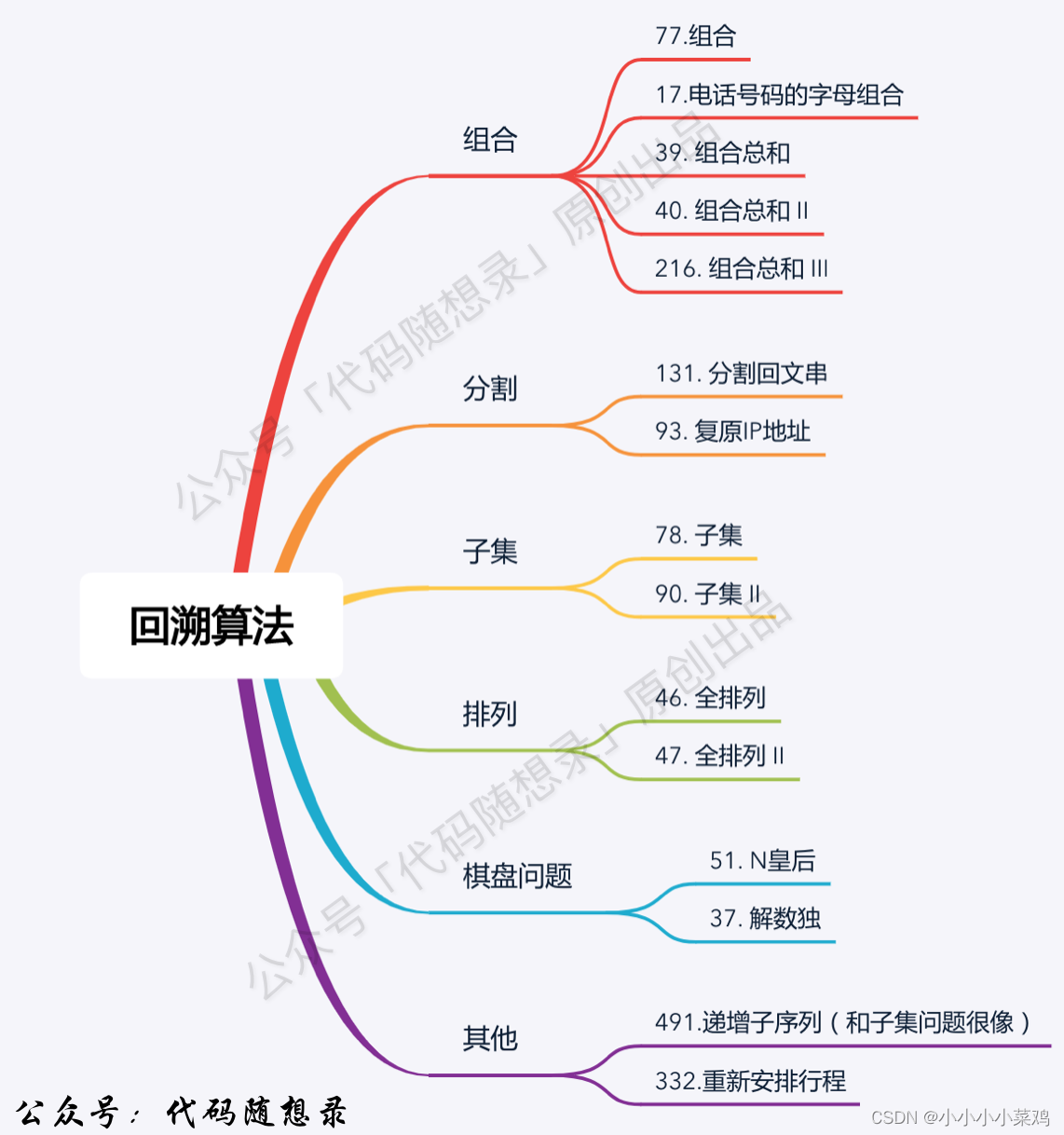
回溯法

回溯法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等
  

如何理解回溯法

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

回溯算法模板框架如下：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

树枝去重树层去重

回溯法去重

什么时候去重？

集合中含有重复元素

树层去重

数组used[i-1]：回溯函数的参数

1. 排序集合。

2. 树层重复：

   i > startIndex && nums[i]==nums[i-1] && used[i-1]==false 
   

startIndex：回溯函数的参数

1. 排序

2. 树层重复：

   i > startIndex && nums[i]==nums[i-1] && used[i-1]==false 
   

   用Set的对象uset：局部变量

   1. uset.coantains(nums[i])
      

   例题

   因为含有重复元素需要去重的有：40. 组合II，90. 子集II， 491. 递增子序列，46. 全排列II。

   其中，491. 递增子序列因为集合必须保留原有顺序，无法排序，又要进行树层去重，所以必须用uset去重。

   46. 全排列II见下面的全排列。

   其它细节

   对于组合问题，什么时候需要startIndex呢？

   startIndex来控制for循环的起始位置。

   我举过例子，如果是一个集合来求组合的话，就需要startIndex，例如：回溯算法：求组合问题！ (opens new window)，回溯算法：求组合总和！ (opens new window)。

   如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex，例如：回溯算法：电话号码的字母组合

   注意以上我只是说求组合的情况，如果是排列问题，又是另一套分析的套路。

   什么时候有返回值？

   函数不遍历整棵树，会提前返回时，需要返回值。

   怎么剪枝？

   1. for循环上，所剩元素不足。

      i<=9-（k-path.size())+1
      

   2. 超出目标和。

   子集问题和组合问题

   了子集问题，在树形结构中子集问题是要收集所有节点的结果，而组合问题是收集叶子节点的结果。

   全排列问题

   全排列问题不用startIndex标识开始，每次都从i=0取，只要该元素没取过就行。

   全排列去重-用数组used！！！

   1. 标记元素是否被取过：有重复的全排列必须用used数组。因为当有重复元素时，必须用used[i]标记元素是否被取过。（没有重复元素时，可以判断path.contains(nums[i])，或者用used[i]）
   2. 所以used数组既判断是否被取过，也判断树层去重。