时间序列的平稳性检验

对时间序列的研究和处理，其实也算是有点意思。很多时候就是耍流氓，我们假设它有规律，然后去研究它，等老天开眼的时候，总能找出点东西来自圆其说，嘿嘿。
ARIMA家族的时序模型，总少不了时序稳定性的检测。为什么它要求时序是稳定的呢，因为这个模型是线性的，为了避免非线性因素对预测的不可控影响，我就提前把这些非线性因素给它卡掉，卡掉它就不影响了，然后就可以开心的建模了。
今天就聊聊怎么检测时序的平稳性。

---

1 观察

就是把时序画出来，然后瞅瞅它是不是在某一均值上下摆动，如果是，那就稳了；如果不是，一般不稳；如果有明显的周期性、单调性，那就恭喜你中奖，绝对不稳，需要差分。

---

2 ACF、PACF

观察法这玩意虽然不用动手，保护了广大开发群众的切身利益，但是总有人质疑啊，万一你带点私人恩怨那就不好了。所以就有人想出来一个好办法：画图，画时序的ACF与PACF，图画出来总能一目了然了吧。

2.1 ACF

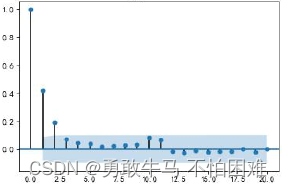
• ACF截尾。即自相关系数最终趋于0，截断点是第几个点，q就是几。这时候说明时序是稳定的。
• ACF拖尾-三角对称。说明时序具有单调性。
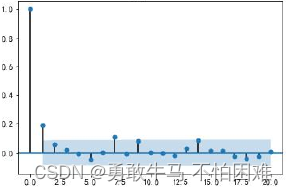
• ACF拖尾-正弦波动。说明时序具有周期性。

截尾(q=7):

拖尾(正弦波动):

2.2 PACF

仅判断时序稳不稳定，用不到PACF。不多讲，咱也不会。

---

3 屠龙之器 单位根检验

观察也观察了，图也画了，还缺点啥啊，没错就是理论依据。这时候就得祭出单位根检验了。

from statsmodels.tsa.stattools import adfuller

单位根检验，会得到一个pvalue，如果pvalue小于0.05，则拒绝原假设，时序平稳。如果比0.05大很多，就再求一次差分。
这地方需要注意的一点是，每差分一次，就会损失一个序列值，所以求单位根的时候，记得来个dropna把空值去掉。

---

应该就这三种方法了八[doge]