未优化版本代码展示:
class Solution {
public int numDecodings(String s) {
char[]chars=s.toCharArray();
int length=s.length();
//创建dp数组
int[]dp=new int[length];
//初始化
if(chars[0]!='0'){
dp[0]=1;
}
//特殊情况处理
if(length==1){
return dp[0];
}
if(chars[1]!='0'){
dp[1]+=dp[0];
}
int num=(chars[0]-'0')*10+(chars[1]-'0');
if(num>=10&&num<=26){
dp[1]++;
}
//填表
for(int i=2;i<length;i++){
if(chars[i]!='0'){
dp[i]+=dp[i-1];
}
int num1=(chars[i-1]-'0')*10+(chars[i]-'0');
if(num1>=10&&num1<=26){
dp[i]+=dp[i-2];
}
}
return dp[length-1];
}
}
1.状态表示:
在思考线性动态规划的题时,我们一般采用从左到右或者从右到左的思考方式
假设我们现在要求从下标为0到下标为i的数符的解码方式总数,我们可以分为两种情况
(1).下标为i的数符可以直接解码为一个字母
此时我们只需要在前面所有的解码方式后添加一个字目即可,而前面所有的解码方式数为dp[i-1]所以此时获得了dp[i-1]个解码方式
(2).下标为i的数符和下标为i-1的数符两个可以代表一个字母,此时我们只需要在前面所有的解码方式后加上一个字母即可,而此时前面所有的解码方式为dp[i-2]
2.由此我们可以获得状态转移方程如果s[i]!='0'则dp[i]+=dp[i-1]
如果26>=(s[i-1]-'0')*10+(s[i]-'0')>=10 则dp[i]+=dp[i-2]
3.接下来创建好dp数组
4.初始化dp数组,由于状态转移方程需要dp[i-1],dp[i-2],所以需要初始化dp[0]和dp[1]的值,避免出现非法访问的情况
5.根据状态转移方程填写dp数组
6.返回值
根据以上步骤便解决了动态规划的问题
优化:
我们观察上面的代码便能发现初始化dp[1]略显繁琐,所以我们可以通过添加辅助结点的方式进行初始化,这也是动态规划经常使用的优化初始化的方法
代码如下:
class Solution {
public int numDecodings(String s) {
char[]chars=s.toCharArray();
int length=s.length();
//创建dp数组
int[]dp=new int[length+1];
//初始化
dp[0]=1;
if(chars[0]!='0'){
dp[1]=1;
}
//特殊情况处理
if(length==1){
return dp[1];
}
//填表
for(int i=2;i<=length;i++){
if(chars[i-1]!='0'){
dp[i]+=dp[i-1];
}
int num1=(chars[i-2]-'0')*10+(chars[i-1]-'0');
if(num1>=10&&num1<=26){
dp[i]+=dp[i-2];
}
}
return dp[length];
}
}
使⽤这种技巧要注意两个点:
(1).辅助结点⾥⾯的值要保证后续填表是正确的;
(2).下标的映射关系
我们通过添加一个辅助结点,将原来dp数组中的数全部向后移动一个位置
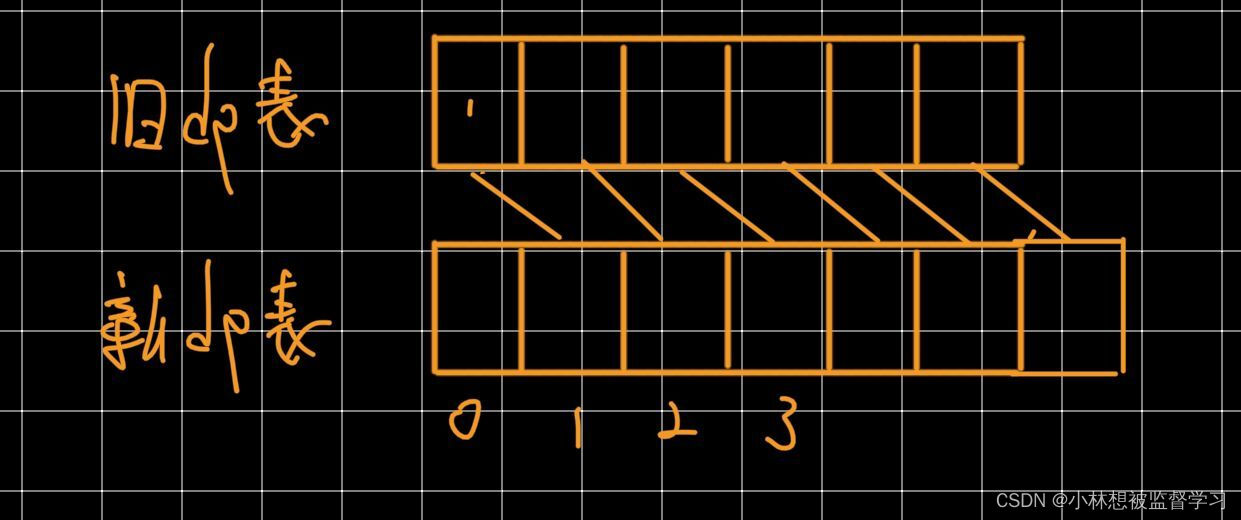
这样我们就可以在循环中给之前较为麻烦的dp[1]进行初始化
而新dp表的dp[0]应该填的数要根据题意来判断,一般是填写0,但该题填写的是1,可以推算一下合适的值当在新dp表中给dp[2]赋值时,当s[1]字符可以表示编码为一个字母,则dp[2]+=dp[1],
当s[0]字符与s[1]字符可以表示编码为一个字母,则dp[2]+=dp[0],而dp[0]要为1才能给dp[2]添加一种编码方式,所以dp[0]应该为1
初始化完成后更改一下新dp表与字符下标之间的映射关系便可完成优化。