---

第六章 图

小题考频：33
大题考频：11

---

6.2 图的存储及基本操作

难度：☆☆☆☆

知识总览

6.2.1 邻接矩阵法

---

6.2.2 邻接表法

---

6.2.3+6.2.4 十字链表、邻接多重表

---

6.2.5 图的基本操作

---

6.2.1 邻接矩阵法

图的存储——邻接矩阵法

1表示两个顶点相互邻接
0表示两个顶点相互不邻接

实现：

定义一个一维数组存放各个顶点的信息。
——用char类型可以放置更复杂的数据。

用二维数组表示各个边的信息。
——因为此处边只有0和1两种状态，可以使用空间更小的bool类型或者枚举类型。
（int型变量可能会占4B或8B，而bool类型或者枚举类型只占1B）

各个结点的数据在数组中有一个具体的编号，Eg.A-0、B-1、C-2……
利用结点在数组中的下标和邻接矩阵里行和列进行对应。

如果矩阵中某一个元素为1，意味着与之对应的边或弧存在，为0则不存在。

无向图：
第i个结点的度=第i行（或第i列）的非零元素个
操作复杂度为$O(n)$

Eg. 要求结点B的度，检查和B对应的这一行，总共有几个非0元素。
可以看到有3个，所以B的度就应该是3。

有向图：
第i个结点的出度=第i行的非零元素个数
第i个结点的入度=第i列的非零元素个数
第i个结点的度=第i行、第i列的非零元素个数之和

---

邻接矩阵法存储带权图（网）

带权图：在对应的位置写上两个顶点之间对应的权值。
如果两个顶点之间不存在边，用无穷表示。

可以定义一个常量INFINITY，取int值的最大值来表示无穷
边的权值可以根据场景改为其他类型

有时带权图中，会把自己指向自己的这条边的权值设为0
在带权图中，如果一条边是无∞或0，则表示与之对应的两个顶点之间不存在边

---

邻接矩阵法的性能分析

 
空间复杂度：$O(|V{|}^2)$——只和顶点数相关，和实际的边数无关

适合用于存储稠密图

如果一个图中顶点数很多，边数很少，那么邻接矩阵中会有很多空间被浪费。

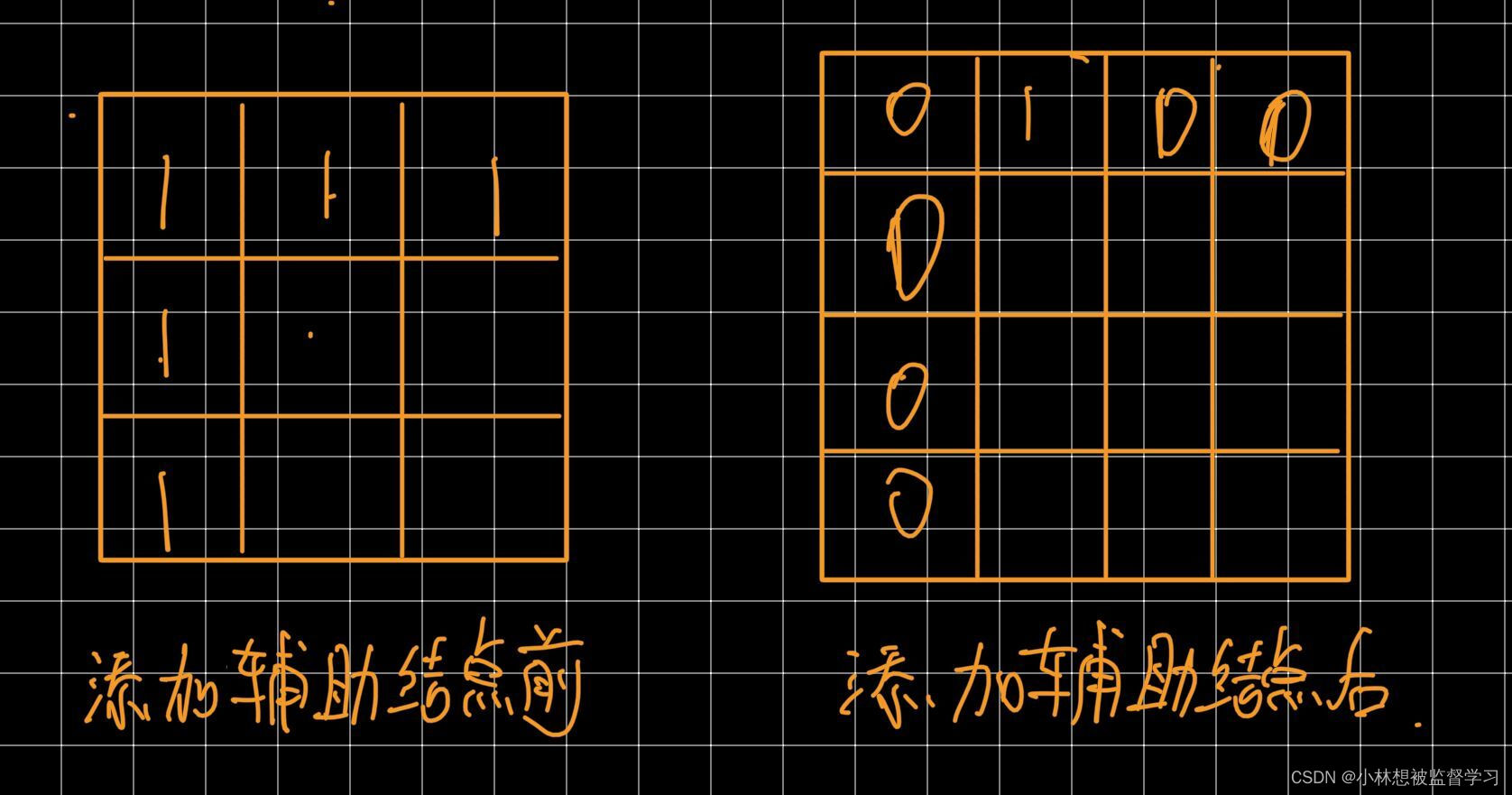
无向图的邻接矩阵是对称矩阵，可以压缩存储（只存储上三角区/下三角区）

回顾：对称矩阵的压缩存储

---

邻接矩阵法的性质

——此处讨论的为不带权图

设图G的邻接矩阵为$A$（矩阵元素为0/1），则$A^n$的元素$A^n\left[i\right]\left[j\right]$等于由顶点$i$到顶点$j$的长度为$n$的路径的数目

此处$A$指的是整个邻接矩阵（右图），其中的某个元素表示由顶点$i$到顶点$j$的长度为$n$的路径的数目。

如果两个矩阵相乘的意义是什么？

Eg. $A^2\left[1\right]\left[4\right]$：第一行和第四列分别相乘相加（式1）
现实意义：
Eg1. 如乘式中的元素$a_{1,2}$为1，意义是结点A到结点B之间有一条边；
与之相乘的元素$a_{2,4}$为1，意义是结点B到结点D之间有一条边；
相乘值为1，意义是存在1条可以从A到B到D的路径。
 
Eg2. 乘式中$a_{1,3}$为0，表示从A到C没有路径；
$a_{3,4}$为0，表示从C到D没有路径；
相乘值为0，那么表示从A到C到D的路径就不存在

所以整个$A^2\left[1\right]\left[4\right]=1$的意义为，从结点A到结点D，只有1条长度为2的路径【A-B-D】

类似，$A^2\left[2\right]\left[2\right]=3$，B到B有3条长度2的路径【BAB、BCB、BDB】

其余分析方法同上。

该矩阵$A^2$的含义为：矩阵中对应的两个结点之间长度为2的路径有多少条

三次方含义类似。
即对应结点之间长度为3的路径有多少条。

更严谨的证明方法详见离散数学图论部分。

---

6.2.2 邻接表法

邻接矩阵（顺序存储）的缺点是：空间复杂度高，为$O(n^2)$，不适合存储稀疏图。

邻接表法（顺序+链式存储）

用一个一位数组存储各个顶点信息：数据域，指向该顶点的第一条边/弧的指针
声明图时，声明顶点结点的一个数组，记录图中共有多少结点、多少边/弧。

对于各边/弧，也有一个与之对应的结点，int adjvex指明了当前这条边/弧指向哪个结点。
——Eg. 如图：AB相连，B的编号为1，所以A之后有一条指向1（结点B）的边，同时也有指向2（结点C）、3（结点D）的边

如果存储带权图，也可以在和边相关的这个顶点中加入权值信息。

对比：树的孩子表示法

邻接表法与树的孩子表示法是相似的

也可以用邻接表法存储有向图：

无向图中，两个相邻的结点会有相同的边。
所以无向图中，边的数据存在冗余：边
结点的数量是$2|E|$，整体空间复杂度为$O(|V|+2|E|)$

有向图中每个结点后的信息表示：从该结点往外射的一条弧
边结点的数量是$|E|$，整体空间复杂度为$O(|V|+|E|)$

无向图的度：遍历和结点相关的边链表，有多少边，度就是多少。
遍历边链表也可以找到该结点相连的所有边。

有向图的度：入度加上出度
出度：遍历和结点相关的边链表，有多少弧，度就是多少。
入度：唯一的办法就是把所有结点的边列表遍历一次，找指向那个结点的弧的数量

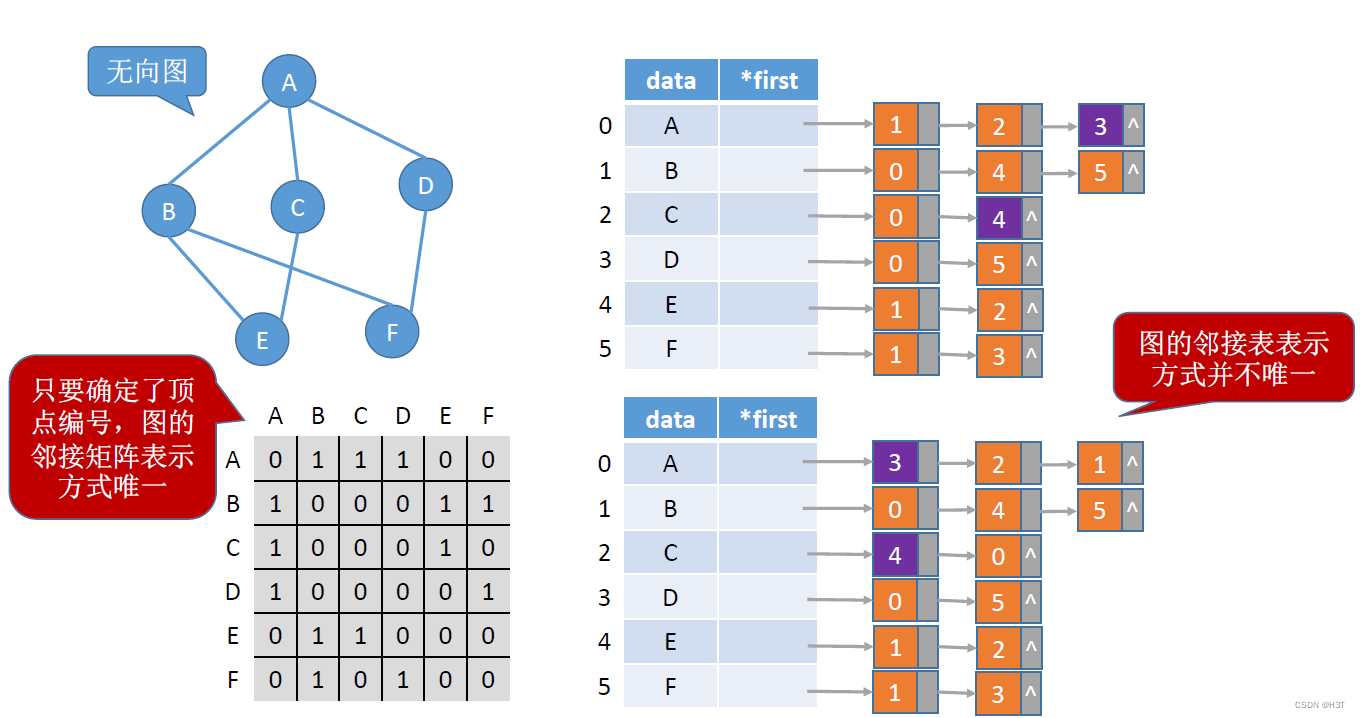
对于一个邻接表，表示方式不唯一。
边在链表中出现的先后顺序是任意的。

而邻接矩阵的表示方式是唯一的！

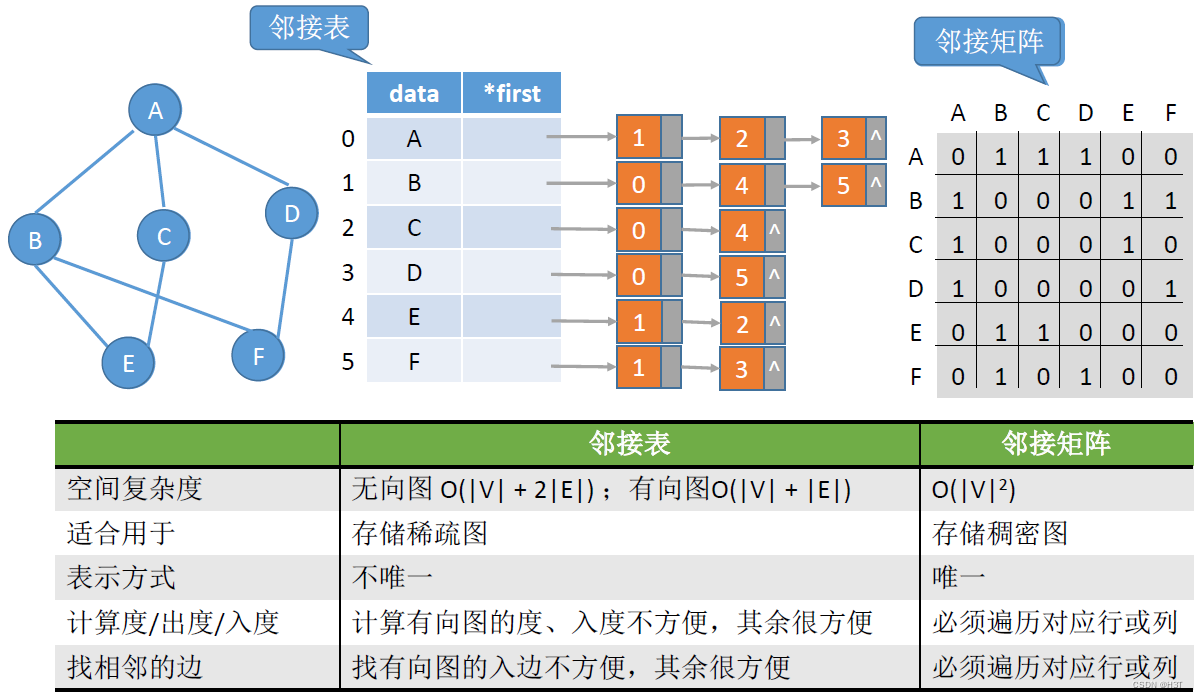
总结：

---

6.2.3+6.2.4 十字链表、邻接多重表

邻接矩阵、邻接表存储有向图都有所不便：

十字链表存储有向图

每一个结点对应一个编号.

十字链表法存储图，定义两个结构体：顶点结点和弧结点

图中顶点结点处的绿色箭头代表该顶点作为弧尾的第一条弧，弧结点的绿色箭头代表弧尾相同的下一条弧
Eg. ①0指向1 A->B ②0指向2 A->C
可以找到所有从当前顶点往外发射的弧

图中顶点结点处的橙色箭头代表该顶点作为弧头的第一条弧，弧结点的橙色箭头代表弧头相同的下一条弧
Eg. ①2指向0 C->A ②3指向0 D->A
可以找到所有指向当前结点的弧

十字链表法找出和入都很方便！

十字链表法性能分析

空间复杂度为$O(|V|+|E|)$，和邻接表同样优秀

如何找到指定顶点的所有出边？——顺着绿色线路找
如何找到指定顶点的所有入边？——顺着橙色线路找

注意：十字链表只用于存储有向图

对无向图的存储能否优化？

邻接矩阵：空间复杂度高
邻接表：数据冗余

---

邻接多重表存储无向图

看图，与十字链表相似
可以定义顶点结点、边结点结构体。
顶点结点：用数组的形式来顺序存储顶点信息。
顶点结点指针：指向和当前顶点相连的第一条边。
边结点：顺着iLink指针往下找，可以找到与当前顶点相连的下一条边。接下来没有更多边与当前顶点相连了，iLink指向NULL。

不用维护两份冗余数据，在删除结点和边的时候操作更方便。

1. 删除边：
   

删除边AB：

需要修改两个指针：让两个节点的指针指向后一条边

2. 删顶点：
   

删除顶点E：

除了删除顶点本身的信息之外，还需要删除和顶点相连的所有边的信息。
并修改指针的值。

更好的空间复杂度，没有冗余边。
删除边、节点都方便。
注意：只适用于存储无向图。

---

6.2.5 图的基本操作

Adjacent(G,x,y)：判断图G是否存在边<x, y>或(x, y)

<>表示有向边（弧）；()表示无向边

Neighbors(G,x)：列出图G中与结点x邻接的边

InsertVertex(G,x)：在图G中插入顶点x

DeleteVertex(G,x)：从图G中删除顶点x

AddEdge(G,x,y)：若无向边(x, y)或有向边<x, y>不存在，则向图G中添加该边

RemoveEdge(G,x,y)：若无向边(x, y)或有向边<x, y>存在，则从图G中删除该边

FirstNeighbor(G,x)：求图G中顶点x的第一个邻接点，若有则返回顶点号。若x没有邻接点或图中不存在x，则返回-1

NextNeighbor(G,x,y)：假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1

Get_edge_value(G,x,y)：获取图G中边(x, y)或<x, y>对应的权值。

Set_edge_value(G,x,y,v)：设置图G中边(x, y)或<x, y>对应的权值为v。

---

知识回顾与重要考点

6.2.1 邻接矩阵法

邻接矩阵法要点回顾：

• 如何计算指定顶点的度、入度、出度（分无向图、有向图来考虑）？时间复杂度如何？
• 如何找到与顶点相邻的边（入边、出边）？时间复杂度如何？
• 如何存储带权图？
• 空间复杂度——$O(|V{|}^2)$，适合存储稠密图
• 无向图的邻接矩阵为对称矩阵，如何压缩存储？
• 设图G的邻接矩阵为A（矩阵元素为0/1），则An的元素An[i][j]等于由顶点i到顶点j的长度为n的路径的数目

---

6.2.2 邻接表法

• 空间复杂度：邻接表空间复杂度低【适合存储稀疏图】；邻接矩阵时间复杂度高【适合存储稠密度】
• 表示方式：邻接表表示方式不唯一；邻接矩阵表示方式唯一‘
• 计算度/入度/出度：邻接表计算有向图的度、入度不方便；邻接矩阵必须遍历对应行或列
• 找相邻边：邻接表找有向图的入边不方便；邻接矩阵必须遍历对应行或列

---

6.2.3+6.2.4 十字链表、邻接多重表

• 理解特性。
• 十字链表只能存有向图
• 邻接多重表只能存无向图

---

6.2.5 图的基本操作