🚀Write In Front🚀
📝个人主页：令夏二十三
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏：AcWing
💬总结：希望你看完之后，能对你有所帮助，不足请指正！共同学习交流 🖊

文章目录

---

前言

        我在大一下时，为了准备蓝桥杯买了AcWing的这套算法基础课，当时只看了前两章的内容，到现在已经隔了好几个月没有练习算法了，模板都生疏了不少，于是想趁暑假有时间，将这套课完整地看完，并记好笔记，在C站上打卡。

        学习课程时，我完整地听完视频，不懂的地方会找题解和博客的思路来理解，每道题的算法模板也会重复敲上三五遍，最后再自己总结笔记。

        今天是我打卡算法学习的第一天，希望接下来可以坚持下去，系统地学完！

        本篇笔记主要介绍了两类基础算法，分别是排序和二分，各自还有细分的算法模板，下面让我们一起学习吧。

一、排序算法

我们都知道有八大排序，但是在这里只介绍两种最常用的算法，分别是快速排序和归并排序。

1. 快速排序

快速排序，简称快排，由于它在诸多排序算法中的时间复杂度最小，因此在程序中使用耗时最短，故称之为快速。

排序，就是将一组无序的数字排成从小到大的有序序列，

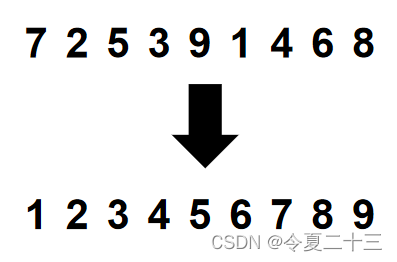
 怎么做呢？不同的排序算法各有其独特思路，快速排序的核心思路就是分治。

分治，就是分而治之，先将无序序列分成 小、中、大 三个部分，从左至右排序，然后对其中的每个部分又按这个方法来排序，先从整体上看有序，到最后最小的细节也有序了，就完成了排序。

具体步骤详解

首先，随机选择序列中的一个数，将其作为排序的分界点：

 然后，在序列中设置指针，分别指向序列的第一个数和最后一个数：

 接下来，如果左边指针所指向的数小于5，则指针向右移动一位，否则停下；若右边指针所指向的数大于5，则向左移动一位，否则也停下。

当两个指针都停下时，交换两个指针所指向的数。

若指针指向的数相同，也就是都移动到了分界点，一次排序就结束了，得到大致有序的序列：

接下来就是对分界点两侧的序列进行同样的排序，每次排序后都可以得到一个更有序的序列，直到序列完全有序：

在实际的代码中，上面的多次细化排序是通过递归实现的。

 代码

#include<iostream>
using namespace std;

const int N=1e6+10;
int n;
int q[N];

void quick_sort(int q[],int l,int r)//l和r分别是数组的左端和右端 
{
	if(l>=r) return;//当数组的右端不大于左端时，可知数组中的数最多只有一个，无需再排序了 
	int x=q[(l+r)/2],i=l-1,j=r+1;//选取x为分界点，i是左指针，j是右指针 
	while(i<j)//当i还在j的左边时，排序尚未结束，需要继续排 
	{
		do i++;while(q[i]<x);//这里的do语句配合了上面i和j的设置，就可以先移动指针，再进行判断 
		do j--;while(q[j]>x);
		if(i<j) swap(q[i],q[j]);//swap函数可以交换数组中下标分别为i和j的位置的数值 
	}
	quick_sort(q,l,j); 
	quick_sort(q,j+1,r);//这里分别对分界点左边部分和右边部分再细致排序 
}

int main()
{
	cin>>n;
	for(int i=0;i<n;i++) cin>>q[i];
	quick_sort(q,0,n-1);
	for(int i=0;i<n;i++) cout<<q[i]<<" ";
	return 0;
}

2. 归并排序

归并排序的中心思想和快排一样，还是分治，但是这里的分治不太一样。

在快排里，我们先排序再递归，而归并则是先递归再排序。

具体步骤详解

归并的过程其实就像它的名字一样，先递归，再合并，合并的过程就是排序的过程。

通过递归，可以将一组无序的序列拆分成若干组只含一个数的序列：

 由图中可看出，每次递归都将序列从中间分成两部分，中间的数归属于左边部分。

接下来，再从递归的最后开始，也就是上图的最后一层开始，逐步将序列两两合并，每次都合并得到一个有序序列，到最后就可以完成排序：

 代码

#include<iostream>
using namespace std;

const int N=1e6;
int n;
int q[N],tmp[N];//这里的tmp数组用来暂存归并后的数组 

void merge_sort(int q[],int l,int r)
{
	if(l>=r) return;
	int mid=(l+r)/2;//mid为数组的中点，用它来将数组分为两部分 
	merge_sort(q,l,mid);
	merge_sort(q,mid+1,r);//用递归的方法将整个数组拆分成一个个只含一个数的序列 
	int k=0,i=l,j=mid+1;//k作为归并数组中的指针 ，i是左边部分的指针，j是右指针 
	while(i<=mid&&j<=r)
	{
		if(q[i]<=q[j]) tmp[k++]=q[i++];//将较小的数先放入归并数组中 
		else tmp[k++]=q[j++];
	}
	while(i<=mid) tmp[k++]=q[i++];//比较完成后，若某个数组还有剩余的数，容易知道它们是有序的，就直接全部移入即可 
	while(j<=r) tmp[k++]=q[j++];
	for(int i=l,j=0;i<=r;i++,j++) q[i]=tmp[j];//最后将归并数组中的数原封不动地放入原数组 
}

int main()
{
	cin>>n;
	for(int i=0;i<n;i++) cin>>q[i];
	merge_sort(q,0,n-1);
	for(int i=0;i<n;i++) cout<<q[i]<<" ";
	return 0;
}