一.概率

事件

若干样本点的集合

事件的概率

等于事件中所有的样本点概率之和

条件概率

贝叶斯定理

 

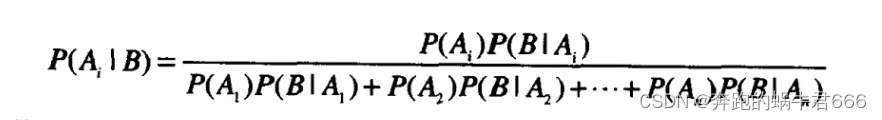
二.离散型概率分布

随机变量

是一次试验的结果的数值性描述

离散型随机变量

指的是有穷个数值或一系列无穷的数值的随机变量

连续型随机变量

代表某一区间或多个区间中的任意数值的随机变量

离散型概率分布

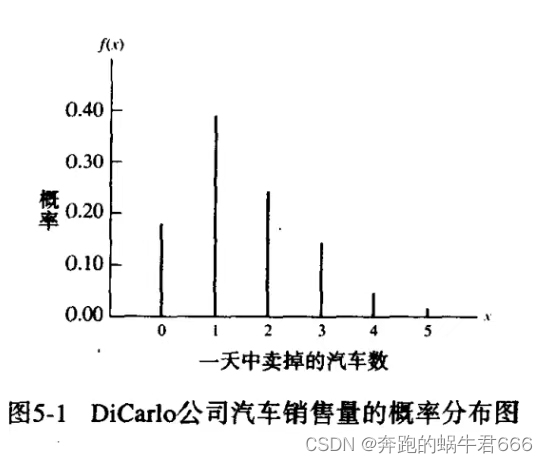
数学期望

随机变量的数学期望或平均值度量随机变量的中心位置

方差

用方差来汇总随机变量值的变异性

二项概率分布

是离散型概率分布

泊松概率分布

泊松随机变量没有上限

超几何概率分布

与二项概率分布很相似，区别是超几何概率分布中的各次试验不是独立的，而且各次试验成功的概率不等 

三.连续型概率分布

均匀概率分布

它是对称概率分布，在相同长度间隔的分布概率是等可能的

正态概率分布

描述连续型随机变量的最重要的概率分布，要求随机变量是连续的

二项概率的正态近似

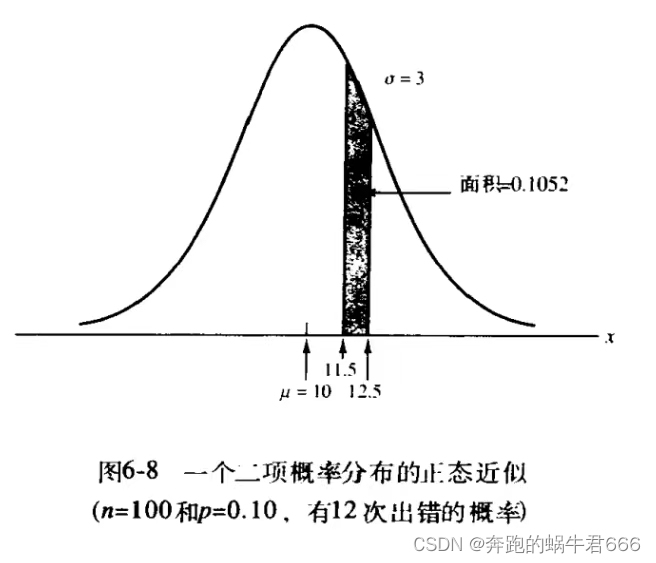
指数概率分布

 

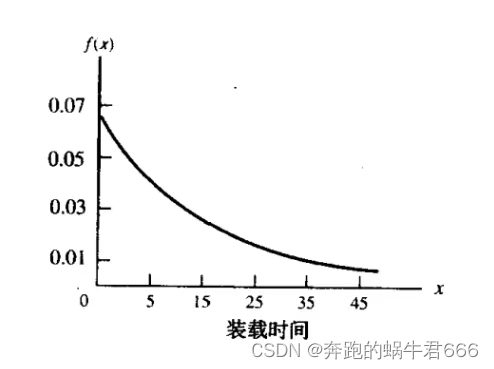
四.抽样与抽样分布

简单随机抽样

指从总体N个单位中任意抽取n个单位作为样本，使每个可能的样本被抽中的概率相等的一种抽样方式

点估计

是用样本统计量来估计总体参数，因为样本统计量为数轴上某一点值，估计的结果也以一个点的数值表示

中心极限定理

从总体中抽取样本容量为n的简单随机样本，当样本容量很大时，样本均值的抽样分布可用正态概率分布近似

五.假设检验

第一类错误和第二类错误

第一类错误是拒绝了实际正确的假设

第二类错误是接受了实际上不成立的假设

犯两类错误的主要影响因素是置信水平，当置信水平越高，即总体之均值落在置信区间的可能性越大，此时越不容易拒绝实际正确的假设，犯第一类的错误的可能性会变小，而犯第二类错误的可能性就会变大；而置信水平越低，越容易犯第一类错误，而不容易犯第二类错误。在实际中我们更怕犯第一类错误，所以会尽量设定高的置信水平

置信区间与置信水平

所谓的统计学，就是依据一个样本来推断总体。在推断过程中，我们或多或少会遇到一些干扰因素，最终推断的结果并不是一个确切的数字，取值会在一个范围里面，这个范围就是所谓的置信区间。

如果要保证总体的取值一定在一个置信区间里，那置信区间的存在也就没什么意义了，因为万事皆有可能，总体的数据可能是任何数，只是概率大不大的问题了，此时置信区间将是一个无尽的区间。所以需要加上置信水平的限制，置信水平给出了一个概率，即不要求百分之百的准确度，只要达到置信水平的标准就行了，我们常用的就是95%的置信水平。比如说95%的置信水平下的置信区间是[2,3]，意思是有百分之95%的可能总体的值出现在[2,3]的区间内。

置信区间[a,b]的计算方法为：（z分数：由置信水平决定，查表得）

a = 样本均值 - z*标准误差

b = 样本均值 + z*标准误差

假设检验的步骤

①确定与应用相适应的原假设和备择假设

②选择检验统计量用于确定是否拒绝原假设

③指定检验中的显著性水平

④利用显著性水平根据检验统计量的值建立拒绝H0的规则

⑤收集样本数据，计算检验统计量的值

⑥将检验统计量的值域拒绝规则所指定的临界值相比较，确定是否拒绝H0，由步骤5中的检验统计量计算p值，利用p值确定是否拒绝H0

区间估计与假设检验的关系

都是根据样本信息推断总体参数；都以抽样分布为理论依据，建立在概率论基础之上的推断；二者可相互转换，形成对偶性。并且这两者还有一定的区别，区间估计是以样本资料估计总体区间的真值。假设检验是以样本资料检验对总体参数的先验假设是否成立。区间估计求得的是求以样本估计值为中心的双侧置信区间，假设检验既有双侧检验，也有单侧检验。区间估计立足于大概率，假设检验立足于小概率

六.简单线性回归

Z 检验

是一般用于大样本（即样本容量大于30）平均值差异性检验的方法

使用标准正态分布理论来推断差异发生的概率，从而比较两个平均数 > 平均数的差异是否显著

T检验

用于样本容量较小（小于30），总体标准差未知的正态分布样本

用来检测数据的准确度，检测系统误差

F检验

在两样本T检验中要用到F检验，检验两个样本的方差是否有显著性差异，这是选择何种T检验（等方差双样本检验，异方差双样本检验）的前提条件

用来监测数据的精密度，检测偶然误差

卡方检验

主要用于检验两个或两个以上样本率或构成比之间差别的显著性，也可以检验两类事物之间是否存在一定的关系