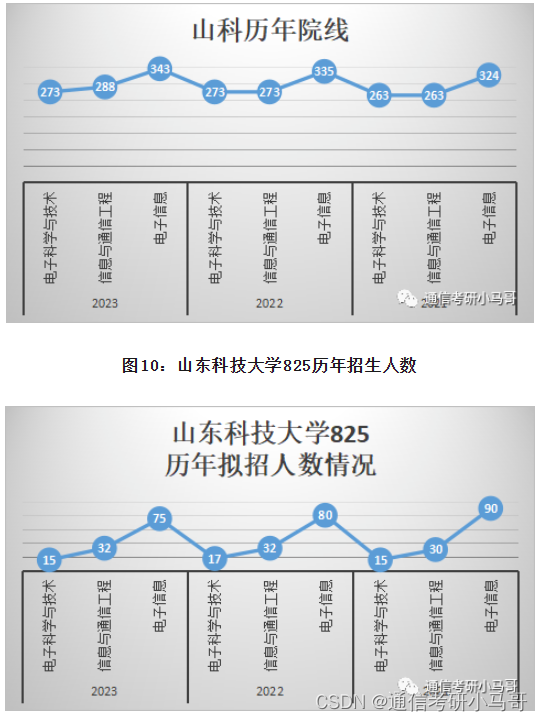
什么是数字签名?
想象一下一下情景:
- Alice生成两个密钥:一个公钥𝑃𝐾𝐴 & 对应的密钥𝑆𝐾𝐴, 发布公钥,保留密钥
- 然后Alice使用𝑆𝐾𝐴 在签名算法中对消息M进行签名,获得签名S,并将(M,S)发送给Bob
- Bob获得𝑃𝐾𝐴 并在验证算法中使用它来验证消息M上的签名S

- 只有签名者本人可以对任意消息生成签名
- 任何人都可以认证签名者对消息的签名
- 密钥对生成算法:签名者使用该算法生成新的私钥和公钥
- 签名算法:该算法以私钥和消息为输入,输出消息的签名
- 验证算法:该算法以公钥、消息以及消息的签名为输入,输出验证结果
数字签名算法具备了 Integrity, Authentication, Non-Repudiation这三个性质。
安全性:对手的能力
默认情况下,对手知道公钥。它是公开的,并且与密钥有关。
- 窃听者可以发现许多消息签名对:已知消息攻击 Known-Message Attack(KMA)
- 但对手可能能够获得他们选择的消息的签名:选择消息攻击 Chosen-Message Attack(CMA)
- 例如,如果对手能够物理访问启用签名的智能卡
- 例如,能够在其选择的消息上查询安全元素的数字签名的恶意软件
安全性:对手的目标
对手的最终目标是找到秘密密钥:密钥恢复 Key Recovery(KR)攻击
- 对手会乐于在特定信息上伪造签名:选择性伪造
- 但对手甚至会乐于在任何信息上伪造签名:存在伪造
- 在某些应用程序中,任何消息都是有效消息,例如,当一方被要求签署随机数以证明其身份时:在这种情况下,在任何新的随机数上找到签名对对手来说就足够了
UF-CMA
对于通用数字签名:
- 最高对抗能力:选择消息攻击 Chosen-Message Attack(CMA)。
- 最容易实现的对手目标:存在伪造
- 此安全级别被称为选择消息攻击下的(存在)不可扩展性 Existential Unforgeability under Chosen-Message Attack(EUF-CMA或简称为UF-CMA)。
- UF-KMA是较低级别的安全。
UF-CMA安全
签名方案有3种算法:
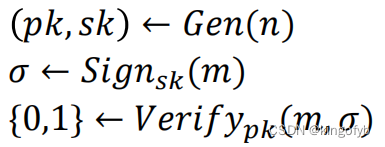
对手被给予pK,并且可以使用Verify算法。
对手有权访问签名。

数字签名 VS MACs
MAC需要安全的密钥共享。签名需要公钥基础设施 Public Key Infrastructure(PKI)。
- 在公钥加密中,密钥管理对各方来说更容易。
- 两者都提供完整性(integrity)和身份验证(authentication)。
- MAC只能私下核实。签名可公开核实。
- MAC不能提供不可否认性。数字签名可以提供。
- 即使Bob与第三方共享MAC密钥,也无法证明Alice制作了MAC标签,因为Bob本可以自己制作。
- 签名可以显示给第三方,他们可以验证。
RSA 家族
教科书RSA签名 - Déjà vu
用两个大素数,然后使𝑛 = 𝑝𝑞, 挑选一对𝑒, d

签名:已给出𝑆𝐾 = 𝑑 和一条消息𝑚 在里面𝑍𝑛 计算签名𝜎

验证:给定一个消息签名对(𝑚, 𝜎) 和公钥𝑃𝐾 = (𝑛, 𝑒) 检查m是否

运行原理:

教科书式RSA 属于UF-CMA吗?
- 对手的目标是伪造:一种新的消息签名对
- 无消息攻击:

对随机消息进行伪造
- 选择消息攻击:

伪造对手想要的任何信息
签署长消息
我们可以将其分解为多个部分,并分别签署每个部分:但是效率比较低下
- 首先对消息进行散列,然后对摘要进行签名:散列和签名

- 哈希不容易反转,对摘要进行验证

如果H被建模为随机Oracle,则哈希RSA是UF-CMA。

哈希冲突会中断不可扩展性
如果两个文档具有相同的哈希,它们将根据相同的签名进行验证!
- 抗冲突是哈希和签名安全所必需的
如果签名是UF-CMA并且H是抗碰撞的,那么Hash和Sign就是UF-CMA。

RSA-PSS
哈希输出(例如256位)比RSA输入(例如2048位)短得多,因此需要将摘要填充到正确的长度
虽然没有已知的攻击,但有一种更强的方案,称为PKCS#1v2.1中标准化的RSA-PSS(概率签名方案)
- 在应用RSA之前使用编码,RSA迭代使用哈希来获得需要小填充的长随机结果
- 概率性:每次对消息进行签名时,签名都不同
- 如果H被建模为随机Oracle,而RSA很难实现,则UF-CMA安全