22运动估计（matlab程序）

news2024/9/17 7:34:53

1.简述

      

实验目的
熟悉运动估计的块匹配（BMA）算法原理，编程实现全搜索算法（三步搜索或钻石搜索算法），了解运动估计在混合编码器中的作用。

实验内容
1）编写全搜索算法函数，将运动矢量叠加到当前帧上并显示输出；
2）显示输出预测帧、残差帧和重建图像，计算预测帧的PSNR。

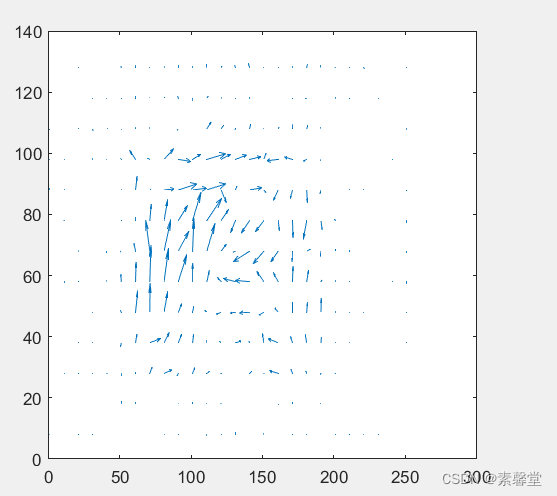
附：可供参考的Matlab函数有hold、quiver

输出图像排列格式如下：

参考帧    当前帧    运动矢量图
预测帧    残差帧    重建帧
 

运动估计的基本思想是尽可能准确地获得序列图像帧间的运动位移，即运动矢量。因为运动估计越准确，预测补偿的图像质量越高，补偿的残差就越小，补偿编码所需位数越少，需要传输的比特率就越小。利用得到的运动矢量在帧间进行运动补偿。补偿残差经过变换、量化、编码后与运动矢量一起经过熵编码，然后以比特流形式发送出去。

在视频编码和处理系统中，运动估计和运动补偿技术对降低视频序列时间冗余度、提高编码效率起着非常关键的作用。运动估计的准确程度将直接决定视频编码器的编码效率。

 

运动估计算法概念

视频原始图像中存在着大量的信息冗余，如时间冗余、空间冗余、信息熵冗余、谱间冗余、几何结构冗余、视觉冗余和知识冗余等等。运动估计是视频压缩编码中的核心技术之一，采用运动估计和运动补偿技术可以消除视频信号的时间冗余以提高编码效率。如何提高运动估计的效率，使运动估计算法的搜索过程更健壮、更快速、更高效成为目前研究的热点。

运动估计的基本思想是尽可能准确地获得序列图像帧间的运动位移，即运动矢量。因为运动估计越准确，预测补偿的图像质量

2.代码

Lucas_Kanade('3.bmp','4.bmp',10)
Lucas_Kanade('1.bmp','2.bmp',10)

 

 

子程序：

function Lucas_Kanade(file1,file2,density);
%% Read Images %%
img1 = im2double (imread (file1));
%% Take alternating rows and columns %%
[odd1, even1] = split (img1);
img2 = im2double (imread (file2));
[odd2, even2] = split (img2);
%% Run Lucas Kanade %%
[Dx, Dy] = Estimate (odd1, odd2);
%% Plot %%
figure; 
[maxI,maxJ]=size(Dx);
Dx=Dx(1:density:maxI,1:density:maxJ);
Dy=Dy(1:density:maxI,1:density:maxJ);
quiver(1:density:maxJ,(maxI):(-density):1,Dx,-Dy,1);
axis square;


%% Run Lucas Kanade on all levels and interpolate %%
function [Dx, Dy] = Estimate (img1, img2)
level = 4;
half_window_size=2;
[m, n] = size (img1);
G00 = img1; G10 = img2;
if (level>0)
    G01 = reduce (G00); G11 = reduce (G10);
end
if (level>1)
    G02 = reduce (G01); G12 = reduce (G11);
end
if (level>2)
    G03 = reduce (G02); G13 = reduce (G12);
end
if (level>3)
    G04 = reduce (G03); G14 = reduce (G13);
end
l = level;

for i=level:-1:0,
    if (l == level)
        switch (l)
        case 4, Dx = zeros (size (G04)); Dy = zeros (size (G04));
        case 3, Dx = zeros (size (G03)); Dy = zeros (size (G03));
        case 2, Dx = zeros (size (G02)); Dy = zeros (size (G02));
        case 1, Dx = zeros (size (G01)); Dy = zeros (size (G01));
        case 0, Dx = zeros (size (G00)); Dy = zeros (size (G00));
        end
    else
        Dx = expand (Dx); Dy = expand (Dy);
        Dx = Dx .* 2; Dy = Dy .* 2;
    end
    switch (l)
    case 4, 
        W = warp (G04, Dx, Dy); 
        [Vx, Vy] = EstimateMotion (W, G14, half_window_size);
    case 3, 
        W = warp (G03, Dx, Dy); 
        [Vx, Vy] = EstimateMotion (W, G13, half_window_size);
    case 2, 
        W = warp (G02, Dx, Dy); 
        [Vx, Vy] = EstimateMotion (W, G12, half_window_size);
    case 1, 
        W = warp (G01, Dx, Dy); 
        [Vx, Vy] = EstimateMotion (W, G11, half_window_size);
    case 0, 
        W = warp (G00, Dx, Dy); 
        [Vx, Vy] = EstimateMotion (W, G10, half_window_size);
    end
    [m, n] = size (W);
    Dx(1:m, 1:n) = Dx(1:m,1:n) + Vx; Dy(1:m, 1:n) = Dy(1:m, 1:n) + Vy;
    smooth (Dx); smooth (Dy);
    l = l - 1;
end


%% Lucas Kanade on the image sequence at pyramid step %%
function [Vx, Vy] = EstimateMotion (W, G1, half_window_size)
[m, n] = size (W);
Vx = zeros (size (W)); Vy = zeros (size (W));
N = zeros (2*half_window_size+1, 5);
for i = 1:m,
    l = 0;
    for j = 1-half_window_size:1+half_window_size,
        l = l + 1;
        N (l,:) = getSlice (W, G1, i, j, half_window_size);
    end
    replace = 1;    
    for j = 1:n, 
        t = sum (N);
        [v, d] = eig ([t(1) t(2);t(2) t(3)]);
        namda1 = d(1,1); namda2 = d(2,2);
        if (namda1 > namda2) 
            tmp = namda1; namda1 = namda2; namda2 = tmp;
            tmp1 = v (:,1); v(:,1) = v(:,2); v(:,2) = tmp1;
        end
        if (namda2 < 0.001)
            Vx (i, j) = 0; Vy (i, j) = 0;
        elseif (namda2 > 100 * namda1)
            n2 = v(1,2) * t(4) + v(2,2) * t(5);
            Vx (i,j) = n2 * v(1,2) / namda2;
            Vy (i,j) = n2 * v(2,2) / namda2;
        else
            n1 = v(1,1) * t(4) + v(2,1) * t(5);
            n2 = v(1,2) * t(4) + v(2,2) * t(5);
            Vx (i,j) = n1 * v(1,1) / namda1 + n2 * v(1,2) / namda2;
            Vy (i,j) = n1 * v(2,1) / namda1 + n2 * v(2,2) / namda2;
        end
        N (replace, :) = getSlice (W, G1, i, j+half_window_size+1, half_window_size);
        replace = replace + 1;
        if (replace == 2 * half_window_size + 2) 
            replace = 1;
        end
    end
end


%% The Reduce Function for pyramid %%
function result = reduce (ori)
[m,n] = size (ori);
mid = zeros (m, n);
m1 = round (m/2); n1 = round (n/2);
result = zeros (m1, n1);
w = generateFilter (0.4);
for j=1:m,
   tmp = conv([ori(j,n-1:n) ori(j,1:n) ori(j,1:2)], w);
   mid(j,1:n1) = tmp(5:2:n+4);
end
for i=1:n1,
   tmp = conv([mid(m-1:m,i); mid(1:m,i); mid(1:2,i)]', w);
   result(1:m1,i) = tmp(5:2:m+4)';
end

%% The Expansion Function for pyramid %%
function result = expand (ori)   
[m,n] = size (ori);
mid = zeros (m, n);
m1 = m * 2; n1 = n * 2;
result = zeros (m1, n1);
w = generateFilter (0.4);
for j=1:m,
   t = zeros (1, n1);
   t(1:2:n1-1) = ori (j,1:n);
   tmp = conv ([ori(j,n) 0 t ori(j,1) 0], w);
   mid(j,1:n1) = 2 .* tmp (5:n1+4); 
end
for i=1:n1,
   t = zeros (1, m1);
   t(1:2:m1-1) = mid (1:m,i)'; 
   tmp = conv([mid(m,i) 0 t mid(1,i) 0], w);
   result(1:m1,i) = 2 .* tmp (5:m1+4)';
end

function filter = generateFilter (alpha)
filter = [0.25-alpha/2 0.25 alpha 0.25 0.25-alpha/2];

function [N] = getSlice (W, G1, i, j, half_window_size)
N = zeros (1, 5);
[m, n] = size (W);
for y=-half_window_size:half_window_size,
    Y1 = y +i;
    if (Y1 < 1)
        Y1 = Y1 + m;
    elseif (Y1 > m)
        Y1 = Y1 - m;
    end
    X1 = j;
    if (X1 < 1)
        X1 = X1 + n;
    elseif (X1 > n)
        X1 = X1 - n;
    end
    DeriX = Derivative (G1, X1, Y1, 'x'); DeriY = Derivative (G1, X1, Y1, 'y');
    N = N + [ DeriX * DeriX, ...
        DeriX * DeriY, ...
        DeriY * DeriY, ...
        DeriX * (G1 (Y1, X1) - W (Y1, X1)), ...
        DeriY * (G1 (Y1, X1) - W (Y1, X1))];
end

function result = smooth (img) 
result = expand (reduce (img));

function [odd, even] = split (img);
[m, n] = size (img);
odd = img (1:2:m, :);
even = img (2:2:m, :);

%% Interpolation %%
function result = warp (img, Dx, Dy)
[m, n] = size (img);
[x,y] = meshgrid (1:n, 1:m);
x = x + Dx (1:m, 1:n); y = y + Dy (1:m,1:n);
for i=1:m,
    for j=1:n,
        if x(i,j)>n
            x(i,j) = n;
        end
        if x(i,j)<1
            x(i,j) = 1;
        end
        if y(i,j)>m
            y(i,j) = m;
        end
        if y(i,j)<1
            y(i,j) = 1;
        end
    end
end
result = interp2 (img, x, y, 'linear');

%% Calculates the Fx Fy %%
function result = Derivative (img, x, y, direction)
[m, n] = size (img);
switch (direction)
case 'x', 
    if (x == 1)
        result = img (y, x+1) - img (y, x);
    elseif (x == n)
        result = img (y, x) - img (y, x-1);
    else
        result = 0.5 * (img (y, x+1) - img (y, x-1));
    end
case 'y', 
    if (y == 1)
        result = img (y+1, x) - img (y, x);
    elseif (y == m)
        result = img (y, x) - img (y-1, x);
    else 
        result = 0.5 * (img (y+1, x) - img (y-1, x));
    end
end
 

3.运行结果

267c6ebe9ab54bfb877989cd61518898.png

 2cd9565fe39d4a10a38b449624aa5452.png

 3c09777637f545339fa70e948c5b8191.png

 

f41e9319b8a64059b21fe07e48e136de.png

 

199c03221ed740659535a018d9e7f907.png

 0aa6ba75c7cc4d28947b6d845ab9d67c.png

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/736946.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

使用Llama.cpp在CPU上快速的运行LLM

使用Llama.cpp在CPU上快速的运行LLM

大型语言模型(llm)正变得越来越流行&#xff0c;但是它需要很多的资源&#xff0c;尤其时GPU。在这篇文章中&#xff0c;我们将介绍如何使用Python中的llama.cpp库在高性能的cpu上运行llm。 大型语言模型(llm)正变得越来越流行&#xff0c;但是它们的运行在计算上是非常消耗资源…
阅读更多...
MongoDB教程-5

MongoDB教程-5

复制是跨多个服务器同步数据的过程。复制在不同的数据库服务器上提供数据的多个副本&#xff0c;从而提供冗余并提高数据可用性。复制可防止数据库丢失单个服务器。复制还允许您从硬件故障和服务中断中恢复。通过增加数据拷贝&#xff0c;您可以将其中一个用于灾难恢复、报告或…
阅读更多...
Spring系列4 -- Bean的作用域和生命周期

Spring系列4 -- Bean的作用域和生命周期

目录 1. 案例 2. 作用域定义 2.1 Bean的6种作用域 2.2 设置作用域 3. Sring的执行流程 4. Bean的生命周期 思考: 为什么不是先进行初始化然后再进行设置属性呢? 1. 案例 假设现在有⼀个公共的 Bean&#xff0c;提供给 A ⽤户和 B ⽤户使⽤&#xff0c;然⽽在使⽤的途中…
阅读更多...
【面试】Hbase

【面试】Hbase

逻辑模型 1 NameSpace 命名空间&#xff0c;类似于关系型数据库的database概念&#xff0c;每个命名空间下有多个表。Hbase有两个自带的命名空间,分别是hbase和default, hbase中存放的是HBase内置的表, default表是用户默认使用的命名空间。 2 Region 类似于关系型数据库的表…
阅读更多...
综合 案例

综合 案例

案例1&#xff1a;淘宝焦点图布局 基本结构 1.大盒子我们类名为: tb-pro淘宝广告 2.里面先放一张图片 3.左右两个按钮用链接。左箭头prev 右箭头 next 4.底侧小圆点用ul 类名为pro-nav 注意&#xff1a; 1.如果一个盒子既有left属性也有right属性&#xff0c;则默认会执行lef…
阅读更多...
Nvidia Jetson Orin系列配置教程

Nvidia Jetson Orin系列配置教程

Nvidia Jetson Orin系列配置教程包含Orin系列的安装及配置办法&#xff0c;目前最为推荐的办法是通过Nvidia SDK Manager进行安装&#xff0c;详细内容如下&#xff1a; 法1&#xff1a;通过Nvidia SDK Manager进行安装 1.下载工具 前往Nvidia SDK Manager下载工具 2.安装工…
阅读更多...
Lesson3-3:OpenCV图像处理---图像平滑

Lesson3-3:OpenCV图像处理---图像平滑

图像平滑 学习目标 了解图像中的噪声类型了解平均滤波&#xff0c;高斯滤波&#xff0c;中值滤波等的内容能够使用滤波器对图像进行处理 1 图像噪声 由于图像采集、处理、传输等过程不可避免的会受到噪声的污染&#xff0c;妨碍人们对图像理解及分析处理。常见的图像噪声有高…
阅读更多...
MySQL之CRUD及常见面试题讲解

MySQL之CRUD及常见面试题讲解

目录 一、CRUD是什么 二、什么是SQL注入 三、行转列的使用 四、CRUD中常用关键词 关键词&#xff1a; GROUP BY HAVING ORDER BY 五、聚合函数和连表查询 聚合函数 连表查询 六、DELETE、TRUNCATE、DROP的区别 七、MySQL常见面试题讲解 一、CRUD是什么 CRUD是一个常…
阅读更多...
ARMv8的异常等级（Exception Level）以及执行状态（AArch64/AArch32）

ARMv8的异常等级（Exception Level）以及执行状态（AArch64/AArch32）

目录 1&#xff0c;异常等级&#xff08;Exception Level&#xff09; 2&#xff0c;Execution states&#xff0c;执行状态 AArch64的异常等级 AArch32的异常等级 3&#xff0c;异常等级切换 4&#xff0c;执行状态切换&#xff08;AArch64 <> AArch32&#xff09;…
阅读更多...
文件下载功能（简单粗暴）

文件下载功能（简单粗暴）

文件下载功能 // 模板下载 export const modelLoadInterface (data: any) > {return get<Response>(tsureexapp-exchange/config/points/grant/export.json, data, {skipErrorHandler: true,}); };import {modelLoadInterface} from "/services/CommunicationF…
阅读更多...
山西电力市场日前价格预测【2023-07-11】

山西电力市场日前价格预测【2023-07-11】

日前价格预测 预测明日&#xff08;2023-07-11&#xff09;山西电力市场全天平均日前电价为419.66元/MWh。其中&#xff0c;最高日前价格为490.80元/MWh&#xff0c;预计出现在11: 45。最低日前电价为365.06元/MWh&#xff0c;预计出现在24: 00。 价差方向预测 1&#xff1a;实…
阅读更多...
关于Xxl-job执行器自动注册不了的问题

关于Xxl-job执行器自动注册不了的问题

最近项目里面用到了xxljob&#xff0c;然后按照官方文档自己搭建了一个&#xff0c;发现一个问题&#xff0c;就是执行器自动注册不了&#xff0c;然后一顿百度&#xff0c;发现是这个配置的问题&#xff1a; 这个 xxl.job.executor.appname 是执行器的名称&#xff0c;是要和页…
阅读更多...
Jenkisn远程执行Shell命令

Jenkisn远程执行Shell命令

Jenkisn远程执行gating 1、安装插件 SSH plugin** 系统管理Manage Jenkins->管理插件Plugin Manager->搜索SSH plugin并安装 2、配置 Credentials凭据 系统管理Manage Jenkins->凭据插件Manage Credentials-> 凭据的类型有很多&#xff0c;本次学习用户名与密…
阅读更多...
关于Arduino UNO R3主控板（CH340)驱动问题

关于Arduino UNO R3主控板（CH340)驱动问题

网上买了一个Arduino UNO R3的标准版产品&#xff0c;开始学习智能编程工具。主要是给小孩子提高一点兴趣爱好&#xff0c;还有就是想在创客实验方面找点素材。 问题&#xff1a; 刚拆包安装驱动遇到一个问题&#xff0c;按说明装了Arduino UNO R3主控板驱动&#xff0c;但就是…
阅读更多...
这所院校学硕年年国家线，8人过线，全部录取！保护一志愿！

这所院校学硕年年国家线，8人过线，全部录取！保护一志愿！

一、学校及专业介绍 山东科技大学&#xff0c;简称“山科大&#xff0c;SDUST”&#xff0c;山东省重点建设应用基础型人才培养特色名校和高水平大学“冲一流”建设高校。&#xff08;我也第一次听说冲一流这个概念图片&#xff09; 1.1 招生情况 山东科技大学通信2023年一共…
阅读更多...
【正点原子STM32连载】第五十三章 照相机实验摘自【正点原子】STM32F103 战舰开发指南V1.2

【正点原子STM32连载】第五十三章 照相机实验摘自【正点原子】STM32F103 战舰开发指南V1.2

1&#xff09;实验平台&#xff1a;正点原子stm32f103战舰开发板V4 2&#xff09;平台购买地址&#xff1a;https://detail.tmall.com/item.htm?id609294757420 3&#xff09;全套实验源码手册视频下载地址&#xff1a; http://www.openedv.com/thread-340252-1-1.html# 第五…
阅读更多...
【大学生自动化测试基础selenium】pageObjece

【大学生自动化测试基础selenium】pageObjece

目录 目录 base_page层 common层 read_data.py send_email.py test_log.py page层 page_ECShop_Login.py testcase层 conftest.py test_login.py venv层 pytest.ini run.tests.py requirements.txt 目录 base_page层 # basepage 基础页面层&#xff08;基类&am…
阅读更多...
算法leetcode｜61. 旋转链表（rust重拳出击）

算法leetcode｜61. 旋转链表（rust重拳出击）

文章目录 61. 旋转链表&#xff1a;样例 1&#xff1a;样例 2&#xff1a;提示&#xff1a; 分析&#xff1a;题解&#xff1a;rust&#xff1a;go&#xff1a;c&#xff1a;python&#xff1a;java&#xff1a; 61. 旋转链表&#xff1a; 给你一个链表的头节点 head &#xf…
阅读更多...
Mysql-------SQL：DDL数据定义语言、DDM数据操作语言、DQL数据库查询语言、DQL数据控制语言

Mysql-------SQL：DDL数据定义语言、DDM数据操作语言、DQL数据库查询语言、DQL数据控制语言

MySQL MySQL是一个关系型数据库管理系统&#xff0c;其数据是保存在不同的数据表中&#xff0c;而不是将所有数据放在一个大仓库内&#xff0c;这样就增加了速度并提高了灵活性 SQL MySQL所使用的SQL语言是用于访问数据库的最常用标准化语言&#xff0c; SQL语言可以分为&am…
阅读更多...
JDY-31 蓝牙传输模块的使用、调试和传输

JDY-31 蓝牙传输模块的使用、调试和传输

JDY-31 蓝牙基于蓝牙 3.0 SPP 设计&#xff0c;这样可以支持 Windows、Linux、android 数据透传&#xff0c; 工作频段 2.4GHZ&#xff0c;调制方式 GFSK&#xff0c;最大发射功率 8db&#xff0c;最大发射距离 30 米&#xff0c;支持用户通过 AT 命令修改设备名、波特率等指令…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023